Stability models
Coastal systems may self-organize at various length and time scales. Sand banks, sand waves both in the shelf and at the coastline, sand bars, tidal inlets, beach cusps, cuspate forelands, spits (among others) are morphological features that are frequently dominated by self-organized processes. Stability models are the genuine tool to understand these processes and make predictions on the dynamics of those features.
Contents
Stability: concepts.
The concepts of equilibrium and stability come from Classical Mechanics (see, for example, Arrowsmith and Place, 1992[1]). A state where a system is in balance with the external forcing so that it does not change in time is called an equilibrium position. However, any equilibrium position may be either stable or unstable. If released near a stable equilibrium position, the system will evolve towards such a position. On the contrary, if released near an unstable equilibrium position, it will go far away from this position. For instance, a pendulum has two equilibrium positions, one up (A), another down (B). If released at rest at any position (except at A) the pendulum will start to oscillate (if it is not already in B) and due to friction it will end up at rest at B. Thus, the pendulum will move spontaneously towards the stable equilibrium and far away from the unstable equilibrium.
Similarly, a beach under constant wave forcing is commonly assumed to reach after some time certain equilibrium profile. However, two main assumptions are here involved: i) an equilibrium state exists and ii) the equilibrium is stable. The existence of an equilibrium profile seems to be granted in the books on coastal sciences and the stability of such an equilibrium is implicitly assumed. However, even if an equilibrium profile exists, it is not necessarily stable. This means that the system would ignore such an equilibrium, it would never tend spontaneously to it. Furthermore, several equilibria may exist, some of them stable, some others unstable.
Example
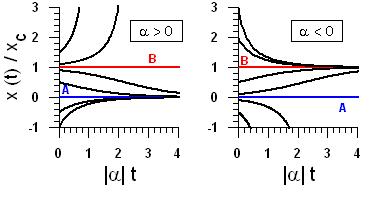
Let us assume a system which is described by only one variable as a function of time, [math]x(t)[/math], and two constant parameters [math] \alpha [/math] and [math] x_c \gt 0 [/math] which are representative of both the characteristics of the system and the external forcing. Assume that this variable is governed by the ordinary differential equation:
[math] \large\frac{dx}{dt}\normalsize = \alpha (x-x_c)x \qquad (1) [/math]
For instance, in a coastal system, [math] \alpha [/math] could represent sediment grain size or wave height, and [math]x(t)[/math] the shoreline displacement at an alongshore location. Given an initial position [math] x(0)=x_0 [/math], the subsequent evolution of the system is described by the solution of the differential equation
[math] x(t) = \large\frac{x_0 x_c}{x_0 +(x_c-x_0) \normalsize \, exp(x_c \alpha t)}\quad (2) [/math]
It becomes clear that the system has two equilibrium positions, A: [math]x=0[/math], and B: [math]x=x_c[/math]. Moreover, for [math] \alpha \gt 0[/math], A is stable while B is unstable. In contrast, A is unstable and B is stable for [math] \alpha \lt 0 [/math]. This is illustrated by Fig. 1 where typical [math]x(t)[/math] solutions are plotted for various initial conditions.
Stability methods: use in coastal sciences.
Equilibrium situations are fundamental in any coastal system as they are the possible steady states where the system can stay under a steady forcing (steady at the time scale which is relevant according to the definition of the system). Then it is crucial to know whether an equilibrium state is stable or not since only stable equilibria can be observed. Furthermore, knowing the conditions for stability of certain equilibrium may be vital when this equilibrium means preserving a beach against erosion, or keeping water depth in a navigation channel. For instance, the entrance of a tidal inlet may be in stable equilibrium under the action of tides and waves. However, if this equilibrium becomes unstable (e.g., because of climate change) the entrance may close up (see section 'Tidal inlets'). Very often, even if the system is out of equilibrium its dynamics can be understood as its path from an unstable equilibrium to a stable one. Therefore, the stability concepts and the mathematical techniques involved are of very general use in coastal sciences. However, stability models are nowadays commonly associated to models for pattern formation. Thus, we will focus here in this broad class of applications which are very often related to that transition from an unstable equilibrium to a stable one.
Coastal and geomorphical systems exhibit patterns both in space and time. Some of these patterns directly obey similar patterns in the external forcing. For example, a beach profile may erode and subsequently recover directly in response to the cycle storm/calm weather in the external wave forcing with the same time scale. This is known as forced behaviour. Other patterns, even if they are driven by some external forcing, do not resemble similar patterns in the forcing. For instance, although bed ripples may be originated by a unidirectional current over a sandy bed, there is nothing in the current itself which dictates the shape, the lengthscale or the characteristic growth time of the ripples. The ripples constitute a new pattern which is not present in the forcing. This is called free behaviour or self-organized behaviour. The forced behaviour is much simpler to predict once the forcing is known. In contrast, predicting the free behaviour is typically much more complicated as it involves the complex internal dynamics of the system itself (see, for instance, Dronkers, 2016[2]).
Stability methods are the genuine tool to describe, understand and model pattern formation by self-organization (Dodd et al., 2003[3]). The typical procedure is to start considering an equilibrium of the system where the pattern is absent (for instance, flat bed, in case of ripples). The key point is that small fluctuations or irregularities are always present (a perfect flat bed or an exact unidirectional, uniform and steady current do not exist). Then, if the equilibrium is stable, any initial small perturbation of the equilibrium will dye away in time. Thus, those small fluctuations will not succeed in driving the system far from the equilibrium (the bed will keep approximately flat). However, if the equilibrium is unstable, there will exist initial perturbations that will tend to grow. Among all of them, some will grow faster than others and their characteristics will prevail in the state of the system. In other words, the patterns corresponding to these initially dominant perturbations of the equilibrium will emerge and will explain the occurrence of the observed patterns (the ripples). However, different patterns may emerge during the instability process and the finally dominant one (the one which is observed) may not correspond to the initially dominant.
When applied to the formation of coastal morphological patterns the instability which leads to the growth is typically originated by a positive feedback between the evolving morphology and the hydrodynamics.
This can operate at different scales and in various environments but a remarkable example at medium scale are the so-called surf zone rhythmic bars which are alongshore periodic or nearly periodic morphological patterns. Their alongshore spacing is of the order of one to a few times the surf zone width, i.e., typically from tens to hundreds of meters, up to maybe one-two km's. A very common source of such patterns is a meandering shore parallel bar which is called crescentic bar. The deepest sections of such a bar are called rip channels. The shallowest sections tend to approach the shore and sometimes attach to it. At the attachment points, the coastline becomes cuspate and this defines what are called mega-cusps. They are different from the 'ordinary' cusps in that those are associated to the shoals at the attachment points which are called transverse bars. However, transverse bars may also exist as elongated shoals connected to the shore (at the corresponding mega-cusps) without any relation with crescentic bars. If their orientation is not exactly shore-normal they are called oblique bars. The equilibrium state to start with is a rectilinear coastline with a bathymetry which is alongshore uniform, either unbarred or with one or more shore-parallel bars. The wave field is assumed to be constant in time. Since the cross-shore profile is assumed to be an equilibrium profile there is no cross-shore net sediment transport. Even if there is longshore transport due to wave oblique incidence, there are no gradients in such transport so that the morphology is constant in time. Now, this equilibrium may be stable or unstable. This means that given a small perturbation on the bathymetry, the wave field will be altered (changes in wave energy distribution, wave breaking, shoaling, refraction, diffraction, etc.), hence the mean hydrodynamics will be altered too (changes in the currents, in set-up/set-down). Therefore, there will be changes in sediment transport thereby appearing convergences/divergences of sediment flux and morphological changes. These morphological changes may either reinforce or damp the initial perturbation. If the latter happens for any perturbation one may consider, the equilibrium is stable and the bathymetry will keep alongshore uniform. If the former happens for at least one possible perturbation, the equilibrium is unstable and the beach will 'spontaneously' (i.e., from the small fluctuations) develop coupled patterns in the morphology, the wave field and the mean hydrodynamics other than the featureless equilibrium. These patterns may eventually result in the observed rhythmic bars with the corresponding circulation patterns. This has been shown for the case of crescentic bars (Calvete et al., 2005[4]; Dronen and Deigaard, 2007 [5]) and transverse/oblique bars (Garnier et al., 2006[6]).
Stability methods can be used not only to understand and model naturally occurring features but also to analize the efficiency and impact of human interventions. The sand which is dumped in a shoreface nourishment interacts with the natural nearshore bars and may trigger some of the morphodynamic instability modes of the system. Following this idea, Van Leeuwen et al., 2007[7] have applied a morphodynamical stability analysis to assess the efficiency of different shoreface nourishment strategies.
Stability methods: use in long term morphological modelling.
Continental shelf morphological features
The sea bed of the continental shelf is rarely flat. Rather, it is usually covered by a number of different types of morphological features ranging from megaripples to sand waves and sand banks. The latter two may be considered as long term features since the characteristic time for its formation and evolution is of decades or centuries. Their horizontal lengthscale (size and spacing) is of the order of hundreds of m for sand waves and few km's for the sand banks. Their origin has been explained as a morphodynamical instability of the coupling between the sandy bed and the tidal currents (Besio et al., 2006[8]). The equilibrium situation is the flat bed where the tides do not create any gradient in sediment flux. The instability mechanism involves only depth averaged flow in case of sand banks whereas it is related to net vertical circulation cells in case of sand waves. Sand banks may also appear near the coast, in water depths of 5-20 m. In this case they are known as shoreface-connected sand ridges. Their origin has also been explained from an instability but where the tidal currents have little influence. In this case, the instability mechanism is caused by the storm driven coastal currents in combination with a transversely sloping sea bed (Calvete et al., 2001[9], see Sec: 'Example: MORFO25 model'). For a more detailed treatment of continental shelf morphological features see also Sand ridges in shelf seas.
Tidal inlets
Stability analysis has been applied to tidal inlets at different levels. First the dynamics of the cross-sectional area of the entrance with its equilibria, their stability and the possibility of closure has been considered. This is done with very simple parametric descriptions of the gross sand transport by tidal currents and waves that allow to derive simple governing ordinary differential equations (see, for instance, van de Kreeke, 2006[10]). Typical time scales for such a dynamics are (e.g., in case of the Frisian inlet, on the Dutch coast) about 30 years. At a second level, the possible equilibrium bathymetries inside the inlet and their stability can be analyzed. This allows to understand the origin and dynamics of the channels and shoals inside the inlet. It turns out that this sometimes complicated structure (even fractal) of channels and shoals is originated by an instability of the flat topography in interaction with the tidal currents due to frictional torques. The time scale for such an instability is of the order of 1 year (see, e.g., Schuttelaars and de Swart, 1999 [11] and Schramkowski et al., 2004[12]). These channels and shoals scale with the length of the embayment but the stability analysis of the flat bottom topography in interaction with tidal currents also gives instability modes at a smaller scale which correspond to the tidal bars that form at the inlet entrance. The growing perturbations associated to this instability are trapped near the entrance and scale with the width of the inlet (Seminara and Tubino, 2001[13] and van Leeuwen and de Swart, 2004[14]).
Large scale shoreline instabilities
Shorelines characterized by a wave climate with high incidence angle with respect to the shore-normal commonly show a wavy shape, cuspate landforms and spits (Classification of sandy coastlines). This can be interpreted as a result of a coastline instability. The littoral drift or total alongshore sediment transport driven by the breaking waves, [math]Q[/math], is a function of wave incidence angle with respect to the shore-normal in deep water, [math]\theta[/math]. It is zero for [math]\theta=0[/math], increases up to maximum for about [math]\theta=\theta_c=43^o[/math] and decreases down to zero for [math]\theta=90^o[/math]. The equilibrium situation is a rectilinear coastline with alongshore uniform nearshore bathymetry and alongshore uniform wave forcing with a [math]\theta[/math] angle. Assume now a small undulation of the otherwise rectilinear coastline consisting of a cuspate foreland. The wave obliquity with respect to the local shoreline is larger at the downdrift side than at the updrift side. Then, if [math]\theta \lt \theta_c[/math], higher obliquity means higher transport so that there will be larger sediment flux at the downdrift side than at the updrift side. This will erode the cuspate shape and the shoreline will come back to the rectilinear equilibrium shape. The shoreline is stable. The contrary will happen if [math]\theta \gt \theta_c[/math] so that the shoreline will be unstable in this case. The instability tends to create undulations of the coastline (shoreline sand waves) with an initial wavelength of about 1-10 km's with a characteristic growth time of the order of a few years (Falqués and Calvete, 2005[15]). Once the initial undulations have grown, the shoreline may evolve towards larger wavelengths and very complex shapes including hooked spits (Ashton et al., 2001[16], see Sec: 'Cellular models').
Linear stability models.
The equations governing coastal systems are typically nonlinear and it is difficult to solve them or to extract useful information from them. However, the small departures from an equilibrium situation approximately obey linear equations that are very useful to determine whether the equilibrium is stable or unstable and, in the latter case, which are the emerging patterns and how fast they grow at the initial stage. For instance, for the equilibrium B ([math]x=x_c[/math]) for equation (1), one may define the departure from equilibrium, [math]z(t)=x(t)-x_c[/math], with governing equation:
[math]\large\frac{dz}{dt}\normalsize = \alpha (x_c+z)z \simeq \alpha x_c z \qquad (3) [/math],
where the last approximation is valid for [math]|z| \ll x_c [/math] and is called linearization. The approximate equation is linear in [math]z(t)[/math] and it is immediately solved to give:
[math]z(t) = z(0) e^{\sigma t}[/math],
where [math]\sigma = \alpha x_c [/math] is called the growthrate and determines whether the perturbation of equilibrium will grow or decay. We recover that B is stable if [math]\alpha \lt 0 [/math] and unstable if [math]\alpha \gt 0 [/math] without solving the nonlinear equation (1).
Steps in developing and using a linear stability model.
- Governing equations.
The first step is to define the variables describing the state of the system. These may be the level of the sea bed as a function of two horizontal coordinates and time, [math]z_b(x,y,t)[/math], or the wave energy density field, [math]E(x,y,t)[/math], or the position of the coastline as a function of a longitudinal coordinate and time, [math] x_s (y,t)[/math], etc. Then, equations expressing the time derivatives of those variables must be derived. For coastal morphodynamic problems these typically constitute a system of partial differential equations in [math]x,y,t[/math] (this was not the case in our extremely simple example where there is a single governing equation which is ordinary in [math]t[/math] or for the model of tidal inlets mentioned above).
- Equilibrium state.
An equilibrium solution of the governing solutions where all the variables of the system are constant in time must be selected. (In our simple example, there are two possible equilibrium solutions.)
- Linearization of the governing equations.
The perturbations with respect to the selected equilibrium solution must be defined, [math] z^,_b(x,y,t) = z_b(x,y,t)-z_{be}(x,y)[/math], [math] E^,_b(x,y,t) = E(x,y,t)-E_e(x,y)[/math], etc. Then, the governing equations must be linearized by neglecting powers higher than one of those perturbations. If the perturbations in all the variables are represented by a vector [math]X(t)[/math], the linearized equations can be represented by: [math]\ dX(t)/dt = B \cdot X(t) [/math] where [math]B[/math] is a linear operator typically involving partial derivatives with respect to the horizontal coordinates, [math]x, y [/math]. (In our simple example, the linearized equation is eq. (3) and operator [math]B[/math] is algebaic and one-dimensional, simply [math]B=\alpha x_c[/math].)
- Solving the linearized equations: eigenvalue problem.
Since the coefficients of the linearized equations do not depend on time, solutions can be found as [math]\ X(t) = e^{\sigma t} \, Z(x,y) [/math] where [math]\sigma [/math] and [math]Z(x,y)[/math] are eigenvalues and associated eigenfunctions of operator [math]B[/math] (note that [math]Z[/math] is [math]n[/math]-dimensional, where [math]n[/math] is the number of variables describing our system). These eigenvalues and eigenfunctions may be complex and only the real part of the latter expression has physical meaning. The equations expressing the eigenproblem are partial differential equations in [math]x,y[/math]. In case where the equilibrium solution is uniform in both [math]x,y[/math] directions (e.g. stability of horizontal flat bed in an open ocean), the coefficients do not depend on these coordinates and wave-like solutions may be found as [math]\ Z(x,y) = A e^{i (K_x x + K_y y)} [/math] where [math]A[/math] is a constant vector. In this case, the eigenvalue problem can be solved algebraically leading to a complex dispersion relation, [math] \sigma = \sigma (K_x,K_y) [/math]. Very often, there is uniformity in one direction, say [math]y[/math], but not in the other. This is typically the case in coastal stability problems where the equilibrium solution depends on the cross-shore coordinate, [math]x[/math], but not on the alongshore one, [math]y[/math]. Thus, the eigenfunctions are wave-like only in the [math]y[/math] direction and are: [math] Z(x,y) = e^{i K_y y} F(x)[/math] In this case, solving the corresponding eigenproblem requieres solving a boundary value problem for ordinary differential equations for [math]F(x)[/math] which is commonly done by numerical methods. In case where the equilibrium state has gradients in any horizontal direction the eigenproblem leads to a boundary value problem for partial differential equations in [math]\ Z(x,y) [/math]. (All this is really trivial in our simple example, because both the governing equation does not involve partial derivatives and vector [math]\ X(t) [/math] is one-dimensional. There is only one eigenvalue, [math]\sigma = \alpha x_c[/math].)
- Analysis of the eigenvalue spectrum: extracting conclusions.
Once the corresponding eigenproblem has been solved, one has a spectrum of eigenvalues [math]\{\sigma_j\}[/math] with the associated eigenfunctions [math]\{ Z_j(x,y)\}[/math]. The [math]j[/math] symbol represents an 'index' to number the eigenvalues, but it is not necessarily discrete. It may be continuous in response to unboundedness of our system in some direction. If the eigenvalue problem has been solved numerically, the numerical eigenvalues are just approximations to the exact eigenvalues. Some of them may even be numerical artifacts that do not have any relation with the exact eigenvalues. These purely numerical eigenvalues are called spurious eigenvalues. Distinguishing between physical and spurious eigenvalues is commonly achieved from physical meaning and from convergence under mesh refinement but may sometimes be quite difficult. The real part of each eigenvalue [math]\Re e(\sigma_j) [/math] determines the growth or decay of the perturbation with shape defined by the associated eigenfunction [math]\{ Z_j(x,y)\}[/math] and is called growthrate. If all the eigenvalues have negative real part, the equilibrium is stable. If there exist at least one positive growthrate, the equilibrium is unstable. If there are a number of eigenvalues with positive growthrate, all the corresponding perturbations can grow. The one with largest growthrate is called the dominant mode and the associated eigenfunction is expected to correspond to the observed emerging pattern in the system. The imaginary part of the eigenvalues is related to a propagation of the patterns. Each eigenvalue with the associated eigenfunction are called normal mode, linear mode or instability mode (the latter in case the growthrate is positive).
Example: MORFO25 model.
This is a linear stability model to identify and explore the physical mechanism which is responsible for the formation of shoreface-connected sand ridges on the continental shelf (Calvete et al., 2001). The model domain is a semi-infinite ocean bounded by the coastline. The governing equations are partial differential equations in time and in both horizontal coordinates which are derived from: i) water mass conservation, ii) momentum conservation and iii) bed changes caused by sediment conservation. The unknowns are the mean sea level, the bottom level and the depth averaged mean current. The sediment transport is directly driven by the current. The equilibrium situation is an alongshore uniform bathymetry consisting of a plane sloping bottom next to the coastline (inner shelf) and a plane horizontal bottom further offshore (outer shelf) together with an alongshore coastal current.
The governing equations are linearized with respect to the perturbations of the equilibrium leading to an eigenvalue problem formulated by means of ordinary differential equations in the cross-shore coordinate only (the equilibrium is uniform along the coast). For each alongshore wavenumber of the perturbation, [math]K_y[/math], these differential equations are discretized by spectral expansions in rational Chebyshev functions so as the eigenvalue problem is set in an algebraic form and is solved by standard subroutines. For each [math]K_y[/math], a spectrum of eigenvalues [math] \{ \sigma_j(K_y), j=1...N \}[/math] with the corresponding eigenvectors is obtained, where [math]N[/math] is the number of freedom degrees of the discretization. The dominant mode for each [math]K_y[/math] is that with largest growthrate, [math]\sigma_M = \Re e (\sigma)[/math]. Now, the dominant pattern is that corresponding to [math]K_y[/math] with maximum [math]\sigma_M (K_y)[/math]. The corresponding spacing, [math] 2\pi/K_y[/math], is of the order of 5 km and the characteristic growth time is of the order of 100 years. The bed patterns are elongated sand ridges which are rotated up current when viewed from the coast. They slowly migrate downcurrent with a speed of a few m per year (given by [math] c = - \Im m (\sigma)/K_y[/math]) (see Fig. 4). All this is consistent with observations (see Sec: 'Continental shelf morphologic features').
Nonlinear stability models.
The linear stability models indicate just the 'initial tendency' to pattern formation starting from small fluctuations of certain equilibrium. This initial tendency involves the shape and horizontal lenghtscales of the pattern but not its amplitude. Also, the shape and lenghtscale at the initial stages may be quite different from the shape at later stages to be compared with observations. Actually, a reliable prediction of pattern formation needs to consider the nonlinear terms which have been neglected in the linearization. This is the aim of nonlinear stability models. Since solving the governing equations can hardly be done analytically, the numerical or approximation method used is essential to them and may be the basis for their classification.
Standard discretized models.
The governing equations can be discretized by standard numerical methods as finite differences, finite elements or spectral methods. This provides algorithms to find an approximation to the time evolution of the system starting from initial conditions. If these initial conditions are chosen as small random perturbations of an equilibrium solution and no linearization has been introduced in the equations, the corresponding code implements a nonlinear stability model since it describes the behaviour of the system when released close to equilibrium.
A possible procedure is the use of existing commercial numerical models (e.g., MIKE21, DELFT-3D, TELEMAC, etc.). This has been done in a number of stability studies (for instance, in case of tidal inlets, see van Leeuwen et al., 2004 or Roelvink, 2006[17]). Their advantage is that they commonly describe the relevant processes as accurately as possible according to present knowledge. However, this typically results in highly complex models with several inconvenients for their use in this context. The most important is that they are typically based on fixed set of equations and discretization methods that the user can not easily change. Furthermore and due to their complexity it is sometimes difficult for the user to exactly know the set of governing equations and parameterizations. In particular, one can not freely turn on/off some of the constituent processes. Another problem may be that the diffusivity which is necessary to keep control of unresolved small scale processes may damp the instabilities to be studied. Moreover, because of their complexity, they are highly time-consuming. Therefore, the use of nonlinear stability models specifically designed may prove to be more efficient to describe a particular pattern dynamics in a particular environment. The most important advantage is that the governing equations, the parameterizations and the discretization methods are more transparent and can be more easily changed. In particular, these models may consider idealized conditions which are suited to exploring certain processes in isolation. Alternatively, one may include more and more processes with the desired degree of complexity and get close to the commercial models. An example of such specific models is MORFO55 which is suited to describe the dynamics of rhythmic bars in the surf zone (Garnier et al., 2006; see Sec: 'Stability methods: use in coastal sciences).
Weakly nonlinear models.
Although direct numerical simulation discussed in last section is very powerful, a systematic exploration of the nonlinear stability properties of a given system needs many runs and may thus be prohibitive. An alternative approach then consists in deriving approximate governing equations based on multiple-scale developments which are called amplitude equations. Apart from their simplicity, the big advantage is that they are generic, i.e., they have the same structure for many different physical systems. Thus, they allow for obtaining general properties in a much cheaper way than by direct numerical simulation. They have however an essential limitation which is stated as follows. The stability or instability of equilibrium depends on the parameters describing the external forcing and the properties of the system. Typically, a single parameter can be defined, [math]r[/math], such that below some threshold or critical value, [math] r\lt r_c [/math], the equilibrium is stable whereas it is unstable above it, [math] r\gt r_c [/math]. Then, if [math] \epsilon = (r-r_c)/r_c [/math] is defined, amplitude equations are restricted to slightly unstable conditions, i.e., [math] 0 \lt \epsilon \ll 1 [/math], the so-called weakly nonlinear regime.
If the eigenvalue spectrum is discrete, it can be assumed for slightly unstable conditions that there is only one eigenvalue of the linear stability problem which has positive real part. i.e., only one instability mode. This means that starting from arbitrary small perturbations of equilibrium, the time evolution of the system will be dominated by this mode, i.e., [math]X(t) \simeq exp(\sigma t) Z(x,y)[/math] which means an exponential growth of the pattern defined by [math]Z(x,y)[/math] according to the real part of the eigenvalue. However, the latter expression gives just an indication but can not be the solution because of the nonlinear terms. A procedure to find an approximate solution begins by realizing that for [math]\epsilon \to 0[/math] the real part of the eigenvalue tends to 0 so that it can read: [math]\sigma = i \omega_c + \epsilon^2 \sigma^, [/math] where [math]\sigma^, = O(1)[/math] and the power two can always be introduced by redefining parameter [math]r[/math] if necessary. This leads to defining a slow time as [math]T=\epsilon^2 t[/math] and to look for an approximate solution of the form [math]X(t) = \epsilon A(T) exp(i\omega_c t) Z(x,y) [/math] where [math]A(T)[/math] is a complex amplitude and the terms on the right of it correspond to the linear eigensolution for [math]\epsilon=0[/math]. By considering that this is just the first term of a power expansion in [math]\epsilon[/math] the so-called Landau equation is obtained for the amplitude:
[math]\large\frac{d A}{dt}\normalsize = \sigma^, A - \beta |A|^2 A[/math]
where [math]\beta[/math] is a coefficient which depends on the system under investigation. When the real part of [math]\beta[/math] is positive, the solutions tend to a new equilibrium characterized by a finite amplitude; then, if [math]\omega_c \ne 0[/math] this solution represents a travelling finite amplitude wave. If the real part of [math]\beta[/math] is negative, explosive behaviour occurs, i.e., the amplitude becomes infinte in a finite time.
Very often, the spectrum is continuum. In this case, for slightly unstable conditions there is a narrow band of eigenvalues with positive real part even for very small [math]\epsilon[/math]. A similar development can be carried out in this case but now, slow spatial coordinates [math]\hat x = \epsilon x [/math] and/or [math]\hat y = \epsilon y[/math] must be defined and the complex amplitude depends on it/them. The generic governing equation is the so-called Ginzburg-Landau equation which is a partial differential equation in T and the slow spatial coordinates.
In practice, the big difficulty of using such methods is the computation of the coefficients (e.g., [math]\beta[/math]) from the original governing equations which can be a tremendous task for the complex coastal systems (see Komarova and Newell[18] for an example). An alternative approach is assuming that the governing equations already are of Ginzburg-Landau type and derive the coefficients from field observations. Then, the resulting equations may be used to make predictions.
Eigenmode expansions.
A possible method for direct numerical simulation is the use of spectral methods which are based on truncated expansions in basis functions of the spatial coordinates. On the other hand, weakly nonlinear methods show that for slightly unstable conditions the spatial patterns are close to those predicted by linear stability analysis. Thus, it is plausible that the spatial patterns of the system may be expressed as a combination of eigenfunctions even for non weakly unstable regime if all the linear instability modes are incorporated:
[math]X(t) = \sum_{j=1}^N A_j(t) Z_j(x,y) [/math]
By inserting this ansatz into the governing equations and by doing a Galerkin-type projection a set of N nonlinear ordinary differential equations for the unknown amplitudes is obtained. This system is then solved numerically. In other words, these methods essentially are spectral Galerkin methods but instead of using expansions in a mathematically defined basis (trigonometric functions, Chebyshev polynomials, etc.) the eigenmodes are used. The set of eigenfunctions to use in the expansion (here symbolically indicated by N) must always contain at least those with positive growthrate but the choice of the additional ones is by no means trivial.
Although there are no a priori restrictions on the applicability of this method (e.g., weakly nonlinear regime), the state of the system must be in practice relatively close to the starting equilibrium in order its behaviour can adequately be described in terms of the eigenfunction set. Thus, this type of models could be classified as 'moderately nonlinear'. Examples of their application are shoreface-connected sand ridges (Calvete and de Swart, 2003[19]) and tidal inlets (Schramkowski et al., 2004).
Cellular models.
In the linear/nonlinear models considered sofar the coastal system is considered as a continuum and the governing equations are set as partial differential equations from the fundamental physical laws as conservation of mass, momentum, energy, wave phase, etc. Either the full equations or the linearized version are subsequently discretized to be solved by numerical methods. The numerical approximations give rise to algorithms to obtain information on the time evolution of the system and these algorithms are finally codified.
An alternative option is to consider the discrete structure of the system from the very beginning. The system is assumed to be governed partially by some of the fundamanental physical laws and partially by some abstract rules which define its behaviour. These rules and laws are directly set in a numerical or algorithmic manner rather than expressing them as partial differential equations. The algorithms giving the time evolution of the system are finally codified. This type of models are known as cellular models because the discretization is inherent to the model itself. It is also sometimes known as self-organization models. The latter is however misleading since self-organization is a type of behaviour of the system and is independent of the model used to describe it.
Cellular models have been applied to explore the self-organized formation of beach cusps (see Coco et al., 2003[20] and references herein.) A very relevant example for long-term morphodynamic modelling is the cellular model of Ashton et al., 2001, to study shoreline instabilities due to very oblique wave incidence. The model domain represents a plan view of the nearshore which is discretized into cells or 'bins'. Each cell is assigned a value, F, [math]0 \le F \le 1 [/math], representing the cell's plan view area that is occupied by land. [math]F=1[/math] represents dry land, [math]F=0[/math] represents ocean cells and [math]0\lt F\lt 1[/math] corresponds to shoreline cells. At each time step, the model updates the shoreline position according to alongshore gradients in littoral drift and sediment conservation similarly to one-line shoreline models. The model allows however for arbitrarily sinuous shorelines, even doubling back on itself and with 'wave-shadow' regions. So, starting from small fluctuations of the rectilinear coastline equilibrium the model can go a long reach and can therefore be considered as strongly nonlinear (see Sec: 'Large scale shoreline instabilities').
Related articles
- Rhythmic shoreline features
- Principles of spontaneous bedform generation
- Wave ripples
- Wave ripple formation
- Sand ridges in shelf seas
- Beach Cusps
- Nearshore sandbars
References.
- ↑ D. K. Arrowsmith and C. M. Place, 1992. "Dynamical Systems". Chapman and Hall/CRC.
- ↑ J. Dronkers, 2016. "Dynamics of Coastal Systems, second edition". World Scientific Publ Co., 700pp .
- ↑ N. Dodd, P. Blondeaux, D. Calvete, H. E. de Swart, A. Falqués, S. J. M. H. Hulscher, G. Rózynski and G. Vittori, 2003. "The use of stability methods in understanding the morphodynamical behavior of coastal systems". J. Coastal Res., 19, 4, 849-865.
- ↑ D. Calvete, N. Dodd, A. Falqués and S. M. van Leeuwen, 2005. "Morphological Development of Rip Channel Systems: Normal and Near Normal Wave Incidence". J. Geophys. Res., 110, C10006, doi:10.1029/2004JC002803.
- ↑ N. Dronen and R. Deigaard, 2007. "Quasi-three-dimensional modelling of the morphology of longshore bars". Coast. Engineering, 54, 197-215.
- ↑ R. Garnier, D. Calvete, A. Falqués and M. Caballeria, 2006. "Generation and nonlinear evolution of shore-oblique/transverse sand bars". J. Fluid Mech., 567, 327-360.
- ↑ S.Van Leeuwen, N.Dodd, D. Calvete and A. Falqués, 2007. "Linear evolution of a shoreface nourishment". Coast. Engineering, in press, doi:10.1016/j.coastaleng.2006.11.006.
- ↑ G.Besio, P.Blondeaux and G. Vittori, 2006. "On the formation of sand waves and sand banks". J.Fluid Mech., 557, 1-27.
- ↑ D. Calvete, A. Falqués, H. E. de Swart and M. Walgreen, 2001. "Modelling the formation of shoreface-connected sand ridges on storm-dominated inner shelves". J. Fluid Mech., 441, 169-193.
- ↑ J. van de Kreeke, 2006. "An aggregate model for the adaptation of the morphology and sand bypassing after basin reduction of the Frisian Inlet". Coast. Engineering, 53, 255-263.
- ↑ H. M. Schuttelaars and H. E. de Swart, 1999. "Initial formation of channels and shoals in a short tidal embayment". J. Fluid Mech., 386, 15-42.
- ↑ G. P. Schramkowski, H. M. Schuttelaars and H. E. de Swart, 2004. "Non-linear channel-shoal dynamics in long tidal embayments". Ocean Dynamics, 54, 399-407.
- ↑ G. Seminara and M.Tubino, 2001. "Sand bars in tidal channels. Part 1. Free bars". J.Fluid Mech., 440, 49-74.
- ↑ S. M. van Leeuwen and H. E. de Swart, 2004. "Effect of advective and diffusive sediment transport on the formation of local and global bottom patterns in tidal embayments". Ocean Dynamics, 54, 441-451.
- ↑ A. Falqués and D. Calvete, 2005. "Large scale dynamics of sandy coastlines. Diffusivity and instability". J. Geophys. Res., 110, C03007, doi:10.1029/2004JC002587.
- ↑ A. Ashton, A. B. Murray and O. Arnault, 2001. "Formation of coastline features by large-scale instabilities induced by high-angle waves". Nature, 414, 296-300.
- ↑ J. A. Roelvink, 2006. "Coastal morphodynamic evolution techniques". Coast. Engineering, 53, 277-287.
- ↑ N.L . Komarova and A. C. Newell, 2000."Nonlinear dynamics of sand banks and sand waves". J. Fluid Mech., 415, 285-321.
- ↑ D. Calvete and H. E. de Swart, 2003. "A nonlinear model study on the long-term behaviour of shoreface-connected sand ridges". J.Geophys.Res., 108 (C5), 3169, doi:10.1029/2001JC001091.
- ↑ G. Coco, T. K. Burnet, B. T. Werner and S.Elgar, 2003. "Test of self-organization in beach cusp formation". J. Geophys. Res., 108, C33101, doi:10.1029/2002JC001496.
Please note that others may also have edited the contents of this article.
|


