Littoral drift and shoreline modelling

Littoral drift, the wave-driven longshore transport of sediment, plays a major role in shoreline dynamics. Human-induced modification of littoral drift is a ubiquitous cause of coastal erosion (see Human causes of coastal erosion). Measuring littoral drift in field situations is notoriously difficult and generally subject to great uncertainty. Therefore, model estimates are often used in practice. A simple, popular model is the so-called 1-line model, derived from shallow-water wave theory. In this article a generalized version of this model (called GENESIS ) is presented, together with conditions and prescriptions for practical application.

The One-Line Concept

Figure 1. Shoreline change and associated bottom profiles.

Gradients in longshore sand transport are not the only cause of shoreline change. Changes also arise from cross-shore transport, which can move the shoreline landward or seaward in response to alternating episodes of calm and stormy wave conditions. However, changes in shoreline position usually recover after some time, see for example Shoreline retreat and recovery. Longshore sand transport is therefore the main process determining long-term trends in shoreline change.

The 1-line concept rests on a common observation that the beach profile maintains an average shape that is characteristic of the particular coast, apart from times of extreme change as produced by storms. For example, steep beaches remain steep and gently sloping beaches remain gentle in a comparative sense and in the long term; the deviation from an average beach slope over the total active profile is relatively small.

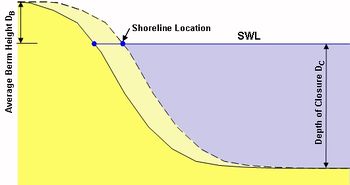
Pelnard-Considere (1956) originated a mathematical theory of shoreline response to wave action under the assumption that the beach profile moves parallel to itself, i.e., that it translates shoreward and seaward without changing shape in the course of eroding and accreting. If the profile shape does not change, any point on it is sufficient to specify the location of the entire profile with respect to a baseline (Fig. 1). Thus, one contour line can be used to describe change in the beach plan shape and volume as the beach erodes and accretes. This contour line is conveniently taken as the readily observed shoreline, and the model is therefore called the "shoreline change" or "shoreline response" model. Sometimes the terminology "one-line" model, a shortening of the phrase "one-contour line" model is used with reference to the single contour line.

Figure 2. Definition sketch for shoreline change calculation.

A second geometrical-type assumption is that sand is transported alongshore between two well-defined limiting elevations on the profile. The shoreward limit is located at the top of the active berm ([math]D_B[/math] in Fig. 1), and the seaward limit is located where no significant depth changes occur, the so-called depth of closure ([math]D_C[/math] in Fig. 1). Restriction of profile movement between these two limits provides the simplest way to specify the perimeter of a beach cross-sectional area by which changes in volume, leading to shoreline change, can be computed. Thus, it is assumed that the beach profile translates seaward or shoreward along a section of shore without changing shape when a net amount of sand enters or leaves the section during a time interval [math]\Delta t[/math]. The change in shoreline position is [math]\Delta y[/math] (Fig. 2) , the length of the shoreline segment is [math]\Delta x[/math], and the profile moves within a vertical extent defined by the height of the berm [math]D_B[/math] and the closure depth [math]D_C[/math]. The change in volume of the section is [math]\Delta V=\Delta x \Delta y (D_B+D_C)[/math], and it is determined by the net rate of sand entering and leaving the section from its two sides. The volume change results if there is a difference in the longshore sand transport rates [math]Q[/math] at the lateral sides of the cells. This net volume change is [math]\Delta V=\Delta Q \Delta t[/math]. Rearrangement of terms yields the governing equation for the rate of change of shoreline position:

[math] \large\frac{\Delta y}{\Delta t}\normalsize + \large\frac{1}{(D_B + D_C)(1-p)} \frac{\Delta Q}{\Delta x}\normalsize = 0 \; . \qquad (1) [/math]

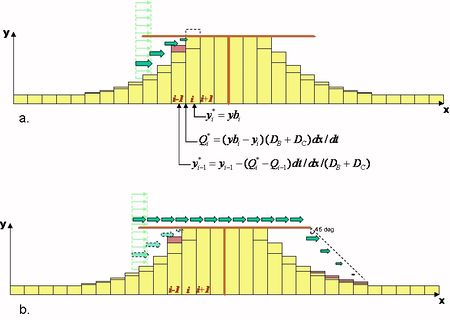
Figure 3 shows the representation of several cells along a coastal stretch downdrift of a short groyne.

Figure 3. Coupled calculation cells alongshore.

The model also requires predictive expressions for the total longshore sand transport rate. For open-coast beaches, the transport rate is a function of the breaking wave height and direction alongshore. The predictive formula for the longshore sand transport rate used in GENESIS is (see the Appendix for a derivation):

[math] Q = {H_{sb}}^2 C_{gb} (a_1 \sin 2 \alpha_b + a_2 \cos \alpha_b \Large\frac {\partial H_{sb}}{\partial x}\normalsize ) \; , \qquad (2) [/math]

in which the subscript [math]_b[/math] denotes the wave breaking location where the depth [math]h=h_b[/math], [math]H_{sb}=[/math] significant wave height at the wave breaking depth contour, [math]C_{gb}=[/math] wave group speed (which is approximately equal to the shallow-water wave celerity [math]C_b=\sqrt{g h_b}[/math]), [math]g=[/math] the gravitational acceleration and [math]\alpha_b=[/math] incidence angle to the wave breaking depth contour. The wave breaking depth contour is assumed parallel to the shoreline. The wave breaking depth [math]h_b[/math] and the wave height [math]H_{sb}[/math] are related by the breaker index [math]\gamma_b = H_{sb} / h_b[/math]. Equation (2) can thus be written

[math] Q = \sqrt{g / \gamma_b} H_{sb}^{2.5} (a_1 \sin 2 \alpha_b + a_2 \cos \alpha_b \Large\frac {\partial H_{sb}}{\partial x}\normalsize) \; . \qquad (3) [/math]

The nondimensional parameters [math]a_1[/math] and [math]a_2[/math] are given by

[math] a_1 = \large\frac {K_1}{32 \, (s - 1)}\normalsize \qquad (4a) [/math]

and

[math] a_2 = \large\frac {K_2}{8 \sqrt{2} (s - 1) \tan \beta}\normalsize \; , \qquad (4b) [/math]

in which [math]K_1[/math] and [math]K_2[/math] are empirical coefficients, treated as a calibration parameters, [math]s=\rho_s/\rho, \; \rho_s =[/math] density of sand (taken to be 2.65 10³ kg/m³ for quartz sand), [math]\rho =[/math] density of water (1.03 10³ kg/m³ for sea water), [math]p =[/math] porosity of sand on the bed (taken to be 0.4), [math]\tan \beta =[/math] average bottom slope. The Coastal Engineering Manual recommends [math]K_1 \approx 0.73[/math].

Representation of Currents

By writing the transport rate in terms of immersed weight, [math]I_l [n/s][/math], Eqs. (1) and (2) may be expressed as,

[math] I_l = (E C_g)_b (K_1 \sin { \alpha_{b}} \cos {\alpha_{b}} - K_2 \Large\frac { \cos {\alpha_{b}}}{ \tan {\beta}} \frac {\partial H_{sb}}{\partial x}\normalsize) \; , \qquad (5) [/math]

where [math]E[/math] is the wave energy density [J/m²]. The classical ‘CERC’-equation for calculating the longshore sediment transport rate is formulated as

[math] I_l = (E C_g)_b K_1 \sin { \alpha_{b}} \cos {\alpha_{b}} \; , \qquad (6) [/math]

which is identical to the first term in the GENESIS transport relation as given in Eq. (2). Following the formula proposed by Bagnold (1963), Eq. (6) can be modified to explicitly represent a longshore current as

[math] I_l = K_3 (E C_g)_b \cos {\alpha_{b}} \Large\frac{v_l}{u_m}\normalsize \; , \qquad (7) [/math]

where [math]K_3[/math] is a dimensionless coefficient, [math]v_l[/math] is the average longshore current in the surf zone, and [math]u_m[/math] is the maximum wave-induced near-bottom horizontal velocity.

By using Eq. (7), the longshore sediment transport rate is no longer restricted to being generated exclusively by breaking waves; the longshore current may originate from other mechanisms as discussed further by Komar and Inman (1970) and Kraus et al. (1982), for example, as generated by the tide or the wind.

If the longshore current [math]v_l[/math] comprises a wave-generated current [math]v_b[/math] alone, it may be calculated as (Lonquet-Higgins 1970, see also Shallow-water wave theory Eqs. (7.18, 7.19))

[math] v_l = v_b = K_4 u_m \sin \alpha_b \; , \qquad (8) [/math]

where [math]K_4[/math] is an empirical coefficient for which Komar and Inman (1970) suggested [math]K_4=2.7[/math]. Thus, with only wave generated currents taken into account, Eqs (6) and (8) together are compatible with the ‘CERC’ equation but are still able to account for currents of different origin.

Along the same lines, Hanson et al. (2001) proposed a generalized version of Eq. (8) which includes the effect of longshore gradients as,

[math] v_b = K_4 u_m \sin \alpha_b - K_5 u_m \large\frac {4}{ \gamma g} \frac {\partial u_m^2}{\partial x} \frac {1}{ \tan \beta}\normalsize \; , \qquad (9) [/math]

where [math]K_5[/math] is an empirical coefficient ([math]=K_2/K_3[/math]). It can easily be shown that in the shallow water limit, Eq. (9) inserted into Eq. (7) reduces back to Eq. (4). Thus, the proposed relationship expressed in Eq. (9) is equivalent to the ‘original’ transport relationship used in GENESIS with only wave-generated transport accounted for.

The coastal current can also be determined from the basic equations describing the wave-driven currents in the surf zone, see Appendix D. These equations can be used to calculate more complex coastal settings. For this, numerical methods must be used, and certain parameters have to be be calibrated to observations.

Representation of Offshore Contours

Figure 4. Impact of predefined offshore contour line.

The wave height and wave incidence angle at the wave breaking depth contour in Eq. (3) have to be specified. Existing wave transformation models including refraction and diffraction can be used for this purpose.

For sufficiently smooth bathymetries, and no significant wave dissipation seaward of the wave breaking depth contour, an analytical expression can be derived relating the wave height [math]H_{sb}[/math] and wave incidence angle [math]\alpha_b[/math] at breaking with the wave height [math]H_s[/math] and incidence angle [math]\alpha[/math] in deep water, where the wave group velocity [math]C_g[/math] is approximately equal to the wave celerity [math]C[/math] (In fact, intermediate deep water is considered, where the depth is still much smaller than the wavelength). The conservation of the cross-shore wave energy flux is used,

[math]H_{sb}^2 C_b \cos \alpha_b = H_s^2 C \cos \alpha \quad[/math] and Snellius' refraction law, [math]\quad \Large\frac{\sin \alpha_b}{C_b}\normalsize = \Large\frac{\sin \alpha}{C}\normalsize .[/math]

Here [math]C \approx \Large\frac{gT}{2 \pi}\normalsize [/math] and [math]C_b \approx \sqrt{g h_b} = \sqrt{g H_b / \gamma_b}[/math].

[math]H_{sb}[/math] and [math]\alpha_b[/math] can be eliminated from these equations if it assumed that the wave incidence angle at breaking is sufficiently small for approximating [math]\cos^{0.2} \alpha_b \approx 1[/math]. Substituting the result in [math]Q = a_1 H_{sb}^2 C_{gb} \sin 2\alpha[/math] gives

[math]Q = Q_1 \, \cos^{6/5} \alpha \, \sin \alpha \, , \quad Q_1 = a_1 2^{0.8} \pi^{-0.2} \gamma_b^{-0.4} g^{0.6} T^{0.2} H_s^{2.4} . \qquad (10)[/math]

However, this methodology has two limitations: 1) dominant local or regional bathymetric features are not well represented, and 2) an open coast without structures or sources or sinks of sediment will evolve to a straight line if the model is run a sufficiently long time. These limitations can be remedied by specifying a fixed representative or effective contour (Hanson and Kraus 1993) which is appended to the feed-back contour associated with local changes in the shoreline (Fig. 4). Correctly specified, the waves transformed over this contour within the GENESIS will maintain a desired overall shoreline curvature, e.g. preserving a bay shape without the presence of structures, even if the model is run for very long time periods.

Representation of Variable Transmission Coefficient for Submerged Breakwaters

Figure 5. Parameters in wave transmission predictive formulas.

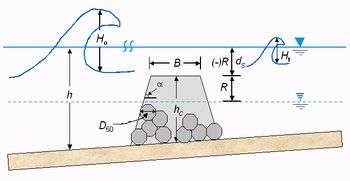
The transmission coefficient is a leading parameter in controlling beach response to detached breakwaters (Hanson and Kraus 1990). Previously the GENESIS model only represented a constant transmission coefficient ([math]K_t=H_t/H_0[/math] in Fig. 5) for detached breakwaters. To improve the predictive capability of the GENESIS model, several published empirical formulae for the wave transmission coefficient were evaluated. In the revised GENESIS, the user may choose either a constant value of [math]K_t[/math] for each structure or allow the model to calculate appropriate values based on time-varying water level and wave height, and structure characteristics. If the variable-[math]K_t[/math] option is selected, water level is read from an input file at a specified input time interval. For each structure, the user specifies geometric properties (crest height and width, slopes on seaward and landward sides, and median rock size) and can select between the calculation methods of Ahrens (2001), Seabrook and Hall (1998), and d'Angremond et al. (1996). The method selected should be based upon structure type and configuration.

Based on the input values describing the structure, water level, and calculated wave properties, a corresponding [math]K_t[/math] is calculated for each structure at each time step. The calculated [math]K_t[/math] will have a strong influence on the wave field behind and adjacent to the structure as it influences wave transmission and diffraction. Through an iterative procedure for calculating wave breaking, [math]K_t[/math] also influences the breaking wave height and direction alongshore, thereby determining the associated shoreline response to the structure (Hanson and Kraus 1989, 1990 , 1991a, 1991b).

Representation of Tombolos

Figure 6. Principle of shoreline and transport correction for tombolo formation.

The boundary condition for representing tombolo formation at T-head groynes and detached breakwaters (DBWs) is formulated analogously to that of a seawall in GENESIS as discussed in Hanson and Kraus (1985). However, implementation of the tombolo constraint is more complex as it includes wave diffraction, blocking of previously open calculation cells, and transport of sediment on both the landward and the seaward sides of the structure. The tombolo concept implies that the beach can reach the structure but not further. As a calculation cell makes contact with the structure, the transport rate into that cell is adjusted to allow the excess sediment to remain in updrift cells. The procedure to do this must conserve sediment volume and preserve the direction of its transport.

The procedure is illustrated in Fig. 6, a plan view of an idealized beach protected by a DBW at an arbitrary moment in time. A tombolo has developed in Cell [math]i+1[/math] in a previous time step. In the adjacent Cell [math]i[/math], allowing the calculated influx [math]Q_i[/math] from Cell [math]i-1[/math] to enter, the shoreline would advance beyond the DBW (Fig. 6a), which is not allowed.

Thus, the initially calculated transport rate [math]Q_6[/math] must be adjusted to [math]Q_6^*[/math] (Fig. 6b) to cause the shoreline to advance up to the detached breakwater but no further, giving [math]y_6^*=y_t[/math]. With the new transport now going out of Cell 5, the shoreline location in this cell will be adjusted from [math]y_5[/math] to [math]y_5^*[/math]. In this particular case, only two cells were recalculated. In the general case, the correction may be carried through any number of cells until the criterion that the shoreline may not advance beyond the DBW is not violated.

Input wave data

Small deviations of the wave input data from the actual wave climate can make a large difference and compromise the quality of model results. Input data directly from observations are rarely available due to the remoteness of the nearest wave buoy. Wave climate data can be retrieved from libraries such as WAVEWATCH, which provide hindcasted deep-water wave records with global coverage (significant wave height, wave direction and wave period at 3-hour intervals). The deep-water data can be extrapolated to the nearshore zone with wave models such as SWAN. Long series of wave data are generally needed to reliably represent the wave climate, including rare extreme conditions that can significantly affect the long-term evolution of the coast. The need for lengthy model runs can be overcome by synthesizing the wave climate in a small number of representative wave conditions and associated durations. Benedet et al. (2016) compared different methods and recommended a method based on sampling the wave climate record according to classes with equal time-integrated deep-water energy fluxes [math]F=C_{g} H_{s}^2[/math]. Wave direction is the mean wave energy flux direction of each class, while wave height is calculated according to the time-integrated wave energy flux, using the mean wave period of the class. By using a morphological acceleration factor, each wave class requires a single model run. The authors showed that in this way a good representation of the wave climate can be obtained with a limited number (order of ten) of wave classes.

Table of symbols

symbol	meaning	symbol	meaning	symbol	meaning
subscript[math]_b[/math]	subscript denoting wave breaking condition	[math]K_1, K_2, K_3, K_4, K_5[/math]	empirical coefficients (calibration parameters)	[math]x \quad [m][/math]	longshore coordinate
[math]C \quad [m/s][/math]	wave celerity	[math]L_0 = g T^2 / (2 \pi) \; [m][/math]	offshore wave length	[math]y (x,t) \quad [m][/math]	shoreline distance from [math]x-[/math]axis
[math]C_g \quad [m/s][/math]	wave group speed	[math]p \approx 0.4[/math]	porosity of sand on the bed	[math]\alpha \quad [rad][/math]	angle of breaking waves to the local shoreline
[math]d_{50} \quad [m][/math]	mean sediment grainsize	[math]Q \quad [m^3/s][/math]	longshore sediment transport	[math]\alpha_b \quad [rad][/math]	wave incidence angle to the breaker line
[math]D=D_B+D_C \quad [m][/math]	sum of berm height and closure depth	[math]s=\rho_s/\rho[/math]	relative density	[math]\tan \beta[/math]	average slope of the surf zone
[math]E=\frac{1}{16} \rho g H_s^2 \quad [J/m^2][/math]	wave energy density	[math]t \quad [s][/math]	time	[math]\gamma_b = H_{sb} / h_b[/math]	breaker index
[math]g \quad [m/s^2][/math]	acceleration due to gravity	[math]T \quad [s][/math]	(peak) wave period	[math]\epsilon \quad [m^2 / s][/math]	diffusion coefficient
[math]h_b \quad [m][/math]	depth at the breaker line	[math]u_m \quad [m/s][/math]	maximum wave-induced near-bottom horizontal velocity	[math]\rho_s \quad [kg/m^3][/math]	sediment density
[math]H_s \quad [m][/math]	significant wave height	[math]v_l \equiv v_0 \quad [m/s][/math]	average longshore current in the surf zone	[math]\rho \quad [kg/m^3][/math]	density of water

Related articles

Stability Models: Linear and nonlinear

Shallow-water wave theory

Rhythmic shoreline features

Human causes of coastal erosion

Coastal Hydrodynamics And Transport Processes

Typical examples of structural erosion

Dealing with coastal erosion

Accretion and erosion for different coastal types

Port breakwaters and coastal erosion

Sand spit

How to apply models

Appendix

A: Derivation of Eq. (2)

Fig. A1. The longshore component of the wave energy flux trough the breaker depth contour per unit contour length is given by [math]F \cos\alpha \sin\alpha[/math].

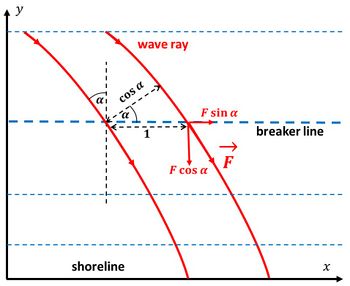
The amount of transmitted wave energy along a wave ray is given by [math]F=C_g E[/math], where [math]C_g[/math] is the wave group speed and [math]E=\frac{1}{16} \rho g H_s^2[/math] the wave energy. Since depth contours are assumed parallel to the shoreline and the wave incidence angle is [math]\alpha[/math], the wave energy flux through a depth contour of unit length is given by [math]F \cos \alpha[/math] (see Fig. A1). The alongshore component of the transmitted wave energy is obtained by multiplying by [math]\sin \alpha[/math]. The product [math]2 \cos \alpha \sin \alpha = \sin 2 \alpha[/math]. Eq. (2) is based on the assumption that the longshore sediment transport is proportional to the alongshore component of the wave energy received at the breaker depth contour per unit contour length. See also Shallow-water wave theory#Longshore Currents for more detailed explanations.

Breaking waves generate an elevation of the mean water level, the so-called wave set-up. This wave set-up is proportional to the wave height [math]H_s[/math] at the breaker contour, according to shallow-water wave theory. If the wave height is variable along the breaker depth contour (the [math]x[/math]-direction), the variable wave set-up will induce a mean longshore current proportional to [math]\partial H_s / \partial x[/math]. It is assumed that the resulting sediment transport (the second term in Eq. (2)) is proportional to this mean longshore current and the wave energy received per unit contour length.

B: Analytical solution for a Gaussian-distributed sand nourishment

The one-line littoral drift model Eq. (1) can be simplified in the case of small wave incidence angles, in such a way that it can be solved analytically. A key assumption underlying Eq. (1) is that cross-shore sediment exchange processes occur on a much smaller time scale than the longshore processes, meaning that on the time scale of the longshore processes the beach profile is always close to equilibrium. It is assumed that alongshore sand transport occurs uniformly along the beach profile down to the closure depth. With these assumptions, the entire coastal profile down to the closure depth moves onshore or offshore, depending on the local coastline position [math]y(x,t)[/math]. The breaker contour line remains parallel to the coastline.

Fig. A2. Wave incidence angles in a 1-line model where the breaker contour line is parallel to the shoreline. [math]\alpha[/math] is the angle of the wave front with the breaker line, [math]\alpha_0[/math] is the angle of the wave front with the [math]x-[/math]axis, [math]\delta[/math] is the angle of the shoreline with the [math]x-[/math]axis.

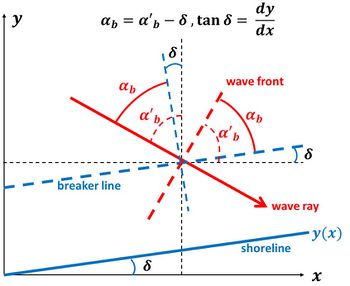
For wave incidence angles [math]\alpha_{b}[/math] (the angle between the wave front and the breaker line, Fig. A2) smaller than about 30° we approximate [math]\sin \alpha_b \approx \alpha_b[/math] and [math]\cos \alpha_b \approx 1[/math]. The approximate expression of the longshore sediment transport Eq. (2) is (neglecting the contribution of longshore gradients in the wave height [math]H \equiv H_{sb}[/math]):

[math]Q = Q_0 \cos \alpha_b \sin \alpha_b \approx Q_0 \, \alpha_b \, , \quad Q_0 = 2 a_1 H_{sb}^2 C_{gb} . \qquad (A1)[/math]

The wave incidence angle [math]\alpha'_b[/math], the angle between the wave front and the [math]x-[/math]axis, is assumed constant. The gradient of the longshore transport is then given by (see Fig. A2)

[math]\Large\frac{\partial Q}{\partial x}\normalsize \approx Q_0 \Large\frac{\partial \alpha_b}{\partial x}\normalsize = - Q_0 \Large\frac{\partial \delta}{\partial x}\normalsize \approx - Q_0 \Large\frac{\partial^2 y}{\partial x^2}\normalsize . \qquad (A2) [/math]

The one-line littoral drift model Eq. (1) then becomes

[math]\Large\frac{\partial y}{\partial t}\normalsize = \epsilon \Large\frac{\partial^2 y}{\partial x^2}\normalsize , \quad \epsilon = \Large\frac{Q_0}{(1-p) D}\normalsize ,\qquad (A3) [/math]

where [math]D=D_B+D_C[/math] is the sum of berm height and closure depth. Equation (A3) is a diffusion equation: initial deviations from a straight shoreline will be gradually spread along the coast. If the initial shoreline position [math]y(x,0)[/math] is known, the solution of Eq. (A3) for the shoreline position [math]y(x,t) , \, t\gt 0 [/math] is given by

[math]y(x,t) = \Large\frac{1}{2 \sqrt{\pi \epsilon t}}\normalsize \int_{-\infty}^{\infty} y(x+\xi, 0) \exp\big(-\large\frac{\xi^2}{4 \epsilon t}\normalsize \big) d \xi . \qquad (A4)[/math]

Fig. A3. Evolution Gaussian-shape nourishment ([math]a = 100 \, m, \; \sigma_0 = 1000 \, m[/math]) with littoral drift ([math]Q_0 = 4 \, 10^5 \, m^3/yr[/math]) and berm height + closure depth [math]D = 8 \, m[/math]. Blue curve: [math]t=0[/math], red curve [math]t=10 [/math] year. No cross-shore sediment transport.

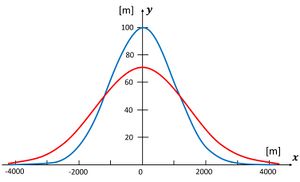
This expression can be integrated analytically for simple shapes of the initial shoreline. An example is the evolution of an initial Gaussian-distributed sand nourishment with cross-shore amplitude [math]a[/math] and longitudinal spread [math]\sigma_0[/math],

[math]y(x,0) = a \exp \big(-\large\frac{x^2}{2 \sigma_0^2} \normalsize \big) . \qquad (A5)[/math]

We assume [math]a \lt \lt \sigma_0[/math], to ensure that the wave incidence angle [math]\alpha[/math] is small over the entire nourishment. We also assume that the cross-shore profile of the nourishment is in morphological equilibrium (no cross-shore sediment transport). The shoreline will then evolve according to

[math]y(x,t) = a \Large\frac{\sigma_0}{\sigma}\normalsize \exp \big(-\large\frac{x^2}{2 \sigma^2}\normalsize \big) , \quad \sigma^2 = 2 \epsilon t +\sigma_0^2 .\qquad (A6) [/math]

The nourishment is not displaced along the shoreline, despite the unidirectional longshore sediment transport [math]Q = Q_0 \, \cos \alpha \sin \alpha[/math] (Fig. A3). It retains its symmetric Gaussian shape, while the squared spread increases linearly with [math]Q_0 t / D[/math]. It does not depend on the wave incidence angle [math]\alpha_0[/math], due to the assumption that this angle is constant and small.

Fig. A4. The evolution of the 21 million m3 ‘sandmotor’ nourishment on the Dutch coast from 2011 (initial state) to 2021. During this period about 10% of the sand was lost from the active coastal zone, 10% was spread to the north (dominant littoral drift direction) and 5% to the south. Image from Huisman et al. (2021).

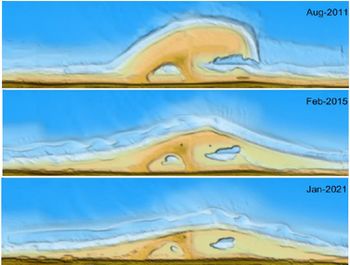
The small angle condition is important. For large angles, a Gaussian sand nourishment acts like a headland. A flying sand spit may develop in downdrift direction from the headland, as discussed in the article Sand spit. Despite this theoretical possibility, no flying spit developed on the sandmotor, the largest beach nourishment in history (21 million m³), see Fig. A4. Due to the dominant northward littoral drift, the amount of sand spread to the adjacent northern coast was about twice the amount spread to the south.

Eq. (A4) can provide estimates of shoreline evolution for many other initial shapes. Several examples are shown in Larson et al. (1987). This report also provides analytical expressions for situations where the longshore sediment transport is not constant, but is modified by the presence of groynes and detached breakwaters. Analytical expressions for the case of beaches of finite length (embayed beaches) are given by Ciccaglione et al. (2023, 2024).

When the wave height [math]H_{sb}[/math] and the wave incidence angle [math]\alpha_b[/math] at the wave breaking contour are expressed in terms of the wave height [math]H_s[/math] and wave incidence angle [math]\alpha[/math] at intermediate deep water, the coefficient [math]\epsilon[/math] in Eq. (A3) has to be replaced by

[math]\epsilon = \Large\frac{Q_1}{(1-p) D}\normalsize \cos^{0.2} \alpha \Big( cos^2 \alpha - \large\frac{6}{5}\normalsize \sin^2 \alpha \Big) ,[/math] were [math]Q_1[/math] is defined in Eq. (10).

C: Other formulas for longshore sediment transport

The uncertainty margins of model estimates of longshore sediment transport are considerable. A factor of 2 between the highest and lowest estimate is not unusual. An analysis of factors inducing uncertainty suggested that, for open coasts, 40% to 50% of the total uncertainty was due to the choice of models that extrapolate offshore wave conditions to wave conditions in the surf zone (wave transformation models). Another 30% to 50% of the uncertainty was due to the choice of longshore sediment transport formulas and the interaction of these models with wave transformation methods.

Several formulas for longshore sediment transport, other than the CERC formula Eq. (2), have been derived from field and laboratory studies. A few formulas that are often used in practice are the empirical formula of Kamphuis (1991)

[math]Q = 1.5 \, 10^{-3} \Large\frac{H_{sb}^3}{T}\normalsize \Big( \Large\frac{H_{sb}}{L_0}\normalsize \Big)^{-1.25} \Big(\Large\frac{H_{sb}}{d_{50}}\normalsize \Big)^{0.25} \big( \tan \beta \big)^{0.75 } \big(\sin (2 \alpha_b) \big)^{0.6}[/math]

and the empirical formula of van Rijn (2014)

[math]Q = K_{vanRijn} 1.8 \, 10^{-4} \, g^{0.5} H_{sb}^{3.1} d_{50}^{-0.6} \big( \tan \beta \big)^{0.4} \sin(2 \alpha_b) ,\qquad K_{vanRijn} = max \Bigg( 1, \; min \Big( 1.5 , \; 1.5 - 10 \big( \Large\frac{H_{sb}}{L_0}\normalsize - 0.01 \big) \Big) \Bigg) [/math]

D: Balance equation longshore current

This appendix reproduces the equations from which the longshore current [math]v_0 \equiv v_l[/math] can be determined using numerical methods. We consider a longshore current driven by a surface wave field [math]\eta_w (x,t)[/math] incident obliquely to the shore of a longshore uniform coast.

Symbols are (attention: [math]x[/math] and [math]y[/math] are swapped her compared to the previous sections!)

[math]x=[/math] shore-perpendicular onshore coordinate, [math]y=[/math] alongshore coordinate , [math]z=[/math] vertical upward coordinate, [math]h=[/math] still water depth, [math]g=[/math] gravitational acceleration, [math]\Big\langle … \Big\rangle \, =[/math]wave-averaged value (averaged over one or more wave cycles, encompassing the turbulence time scale), [math]\; u(x,z,t), \, v(x,z,t), \, w(x,z,t) \,=[/math] shore-normal, longshore, vertical velocity; [math]\; u_0 = \lt u\gt , \, v_0=\lt v\gt , \, w_0=\lt w\gt [/math], [math]\; u_w, \, y_w, \, w_w \,=[/math] shore-normal, longshore, vertical wave orbital velocities, [math]\; u', \, v', \, w' \, =[/math] turbulent velocity fluctuations.

The velocities [math]u, \, v, \, w[/math] and surface elevation [math]\eta[/math] are decomposed as

[math]u = u_0 + u_w + u' \, , \; v = v_0 + v_w + v' \, , \; w = w_0 + w_w + w' \, , \; \eta = \Big\langle\eta \Big\rangle + \eta_w \, , \; d= h + \Big\langle \eta \Big\rangle . \qquad (1)[/math]

The momentum balance equation in the longshore direction is

[math]\dfrac{\partial v}{\partial t} + \dfrac{\partial uv}{\partial x} + \dfrac{\partial v^2}{\partial y} + \dfrac{\partial w v}{\partial z} + \dfrac{1}{\rho}\dfrac{\partial p}{\partial y} = 0 \, , \qquad (2)[/math]

where [math]p=p(x,y,z,t)=[/math] pressure. Integration over the depth and averaging over one or more wave cycles gives

[math]\Big\langle \dfrac{\partial}{\partial x} \int_{-h}^{\eta} uv dz \Big\rangle + \Big\langle \dfrac{\partial}{\partial y} \int_{-h}^{\eta} v^2 dz \Big\rangle + \dfrac{1}{\rho} \Big\langle \int_{-h}^{\eta} \dfrac{\partial p}{\partial y} dz \Big\rangle - \dfrac{1}{\rho } \Big\langle \tau_s - \tau_b \Big\rangle = 0 \, , \qquad (3)[/math]

where [math]\tau_b \approx - \rho \Big\langle v'_b w'_b \Big\rangle \, , \; \tau_s \approx - \rho \Big\langle v'_s w'_s \Big\rangle [/math] and subscripts [math]_b, \, _s[/math] denote values at the seabed [math]z=-h[/math] and the surface [math]z=\eta[/math] respectively. For the permutation of integration and derivation in Eq. (3) we have used the surface and bottom boundary conditions which state that the surface and the seabed are streamlines: [math]\quad W_s=\dfrac{\partial \eta}{\partial t} + U_s \dfrac{\partial \eta}{\partial x} + V_s \dfrac{\partial \eta}{\partial y} \; , \; W_b = - U_b\dfrac{dh}{dx} - V_b \dfrac{dh}{dy} \, , [/math] where [math]U = u_0+u_w \, , \, V = v_0+v_w \, , \, W = w_0+w_w[/math].

Equation (3) is greatly simplified if it is assumed that the coast is uniform in longshore direction, as this eliminates all [math]y-[/math]derivatives. With this assumption, the longshore current is driven by the cross-shore gradient of the wave-induced radiation stress [math]S_{xy} = \Big\langle \int_{-h}^{\eta} \rho u_w v_w dz \Big\rangle \quad[/math], see also Shallow-water wave theory#Radiation Stress Components for Oblique Waves. In linear shallow-water wave theory [math]S_{xy}[/math] is given by [math]S_{xy} = \dfrac{C_g}{C} E \cos \alpha \sin \alpha \, , \quad C_g = \dfrac{C}{2} \Big( 1 + \dfrac{2kh}{\sinh 2kh} \Big) \approx C \approx \sqrt{gh} \, , \quad E = \frac{1}{8} \rho g H^2[/math].

The first term in Eq. (3) can be written [math]\Big\langle \int_{-h}^{\eta} u v dz \Big\rangle = S_{xy} + \Big\langle \int_{-h}^{\eta} u_0 v_0 dz \Big\rangle +\Big\langle \int_{-h}^{\eta} u' v' dz \Big\rangle \, .[/math]

Evaluation of [math]\Big\langle \int_{-h}^{\eta} u_0 v_0 dz \Big\rangle[/math] requires solving the undertow equation, as explained in the article Undertow. The term [math]\Big\langle \int_{-h}^{\eta} u' v' dz \Big\rangle[/math] represents cross-shore diffusion of the longshore current. In a gradient-type diffusion model with diffusion coefficient [math]K_H[/math] this term can be represented by [math]- d \, K_H \partial v_0 / \partial x \, .[/math] The bed stress [math]\tau_b = - \rho \Big\langle v' w' \Big\rangle[/math] can be related through a drag coefficient [math]c_D[/math] to the cross-shore and longshore instantaneous velocities [math]u[/math] and [math]v[/math] in the wave boundary layer, [math]\tau_b = - \rho \Big\langle v' w' \Big\rangle = \rho c_D \Big\langle v \, \sqrt{u^2+v^2} \Big\rangle \, .[/math]

The longshore current for a longshore uniform coast can then be determined numerically from the momentum balance equation

[math] \dfrac{\partial S_{xy}}{\partial x} - \tau_s + \rho \Big\langle \dfrac{\partial}{\partial x} \int_{-h}^{\eta} u_0 v_0 dz \Big\rangle + \rho c_D \Big\langle v \, \sqrt{u^2+v^2} \Big\rangle - \rho \dfrac{\partial}{\partial x} d\, K_H \dfrac{\partial v_0}{\partial x} =0 \, . \qquad (4) [/math]

It is often assumed that the surface shear stress [math]\tau_s[/math] is mainly related to the energy dissipation of the surface roller. The surface roller is a recirculating mixture of water and air generated at the breaking wave crest. The roller is surfing with the wave bore towards the beach with celerity [math]C \approx \sqrt{gh}[/math]. The shear stress generated by the roller can be related to the roller energy [math]E_r[/math] ,

[math]\langle \tau_s \rangle \approx \dfrac{2 \sin \theta }{h} E_r \, ,\quad[/math] where [math]\theta[/math] is the slope angle of the bore front. A more detailed explanation is given in Wave set-up#Effect of the surface roller. The effect of the surface roller is to move the peak of the longshore current inland from the breakpoint, as observed in the field.

References

The main author of this article is Hanson, Hans Please note that others may also have edited the contents of this article. Citation: Hanson, Hans (2025): Littoral drift and shoreline modelling. Available from http://www.coastalwiki.org/wiki/Littoral_drift_and_shoreline_modelling [accessed on 10-05-2025] For other articles by this author see Category:Articles by Hanson, Hans For an overview of contributions by this author see Special:Contributions/Tvrl-hha

Article reviewed by

Job DronkersSee the discussion page