Waves on a sloping bed
This article deals with frictionless, non-breaking shallow water waves propagating in positive [math]x-[/math]direction over a sloping bed with depth [math]h(x) = - \beta x[/math].
A mathematical treatment of this process has been developed by Carrier and Greenspan (1957[1]), which is reproduced below.
The kinematics of wave uprush on an inclined plane are relevant for processes described in the Coastal Wiki articles Swash zone dynamics, Infragravity waves, Wave run-up and Wave overtopping of hydraulic structures.
Contents
Characteristic wave equations
The wave equations read:
[math]\Large\frac{\partial \eta}{\partial t}\normalsize + \Large\frac{\partial (h +\eta) u }{\partial x}\normalsize = 0 \; , \quad \Large\frac{\partial u}{\partial t}\normalsize + u \Large\frac{\partial u}{\partial x}\normalsize + g \Large\frac{\partial \eta}{\partial x}\normalsize = 0\, . \qquad (1)[/math]
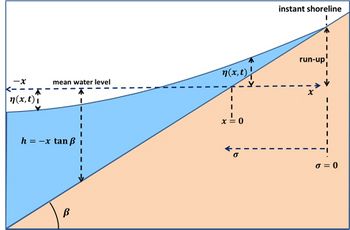
Here is (Fig. 1): [math]\; \eta(x,t)=[/math]wave surface elevation, [math]u(x,t)=[/math]wave orbital velocity, [math]g=[/math]gravitational circulation, [math]\beta \approx \tan \beta =[/math]bed slope, [math]t=[/math]time coordinate.
These equations describe two characteristics waves
[math]p(x,t) = u + 2 c + g \beta t \, , \quad q(x,t) = u - 2 c + g \beta t \,, \quad c = \sqrt{g(\eta + h)} = \sqrt{g(\eta - \beta x)} \qquad (2)[/math]
propagating along characteristic curves, according to the characteristic equations
[math]\Large\frac{dp}{dt}\normalsize = \Large\frac{\partial p}{\partial t}\normalsize + \Large\frac{dx}{dt}\frac{\partial p}{\partial x}\normalsize =0 \, , \; \Large\frac{dx}{dt}\normalsize = u+c \, ; \quad \Large\frac{dq}{dt}\normalsize = \Large\frac{\partial q}{\partial t}\normalsize + \Large\frac{dx}{dt}\frac{\partial q}{\partial x}\normalsize =0 \, , \; \Large\frac{dx}{dt}\normalsize = u-c \, .\qquad (3)[/math]
It can be verified that Eqs. (2, 3) are equivalent to Eq. (1).
Considering [math]p[/math] and [math]q[/math] as new independent variables we can write the characteristic waves as
[math]\Large\frac{\partial p}{\partial q}\normalsize = \Large\frac{\partial }{\partial q}\normalsize (u+2c+g \beta t) = 0 \, , \quad \Large\frac{\partial x}{\partial q}\normalsize = (u+c) \Large\frac{\partial t}{\partial q}\normalsize \, , \qquad (4)[/math]
[math]\Large\frac{\partial q}{\partial p}\normalsize = \Large\frac{\partial }{\partial p}\normalsize (u-2c+g \beta t) =0 \, , \quad \Large\frac{\partial x}{\partial p}\normalsize = (u-c) \Large\frac{\partial t}{\partial p}\normalsize \, . \qquad (5)[/math]
We eliminate [math]x[/math] by cross-differentiation the r.h.s. of Eqs. (4, 5), giving
[math]\Large\frac{\partial (u+c)}{\partial p}\normalsize \Large\frac{\partial t}{\partial q}\normalsize + c \Large\frac{\partial^2 t}{\partial pq}\normalsize =\Large\frac{\partial (u-c)}{\partial q}\normalsize \Large\frac{\partial t}{\partial p}\normalsize - c \Large\frac{\partial^2 t}{\partial pq}\normalsize \, . \qquad (6) [/math]
From the l.h.s. of Eqs. (4,5) we have
[math]\Large\frac{\partial (u+c)}{\partial p}\normalsize = 3 \Large\frac{\partial c}{\partial p}\normalsize - g \beta \Large\frac{\partial t}{\partial p}\normalsize \, , \quad \Large\frac{\partial (u-c)}{\partial q}\normalsize = - 3 \Large\frac{\partial c}{\partial q}\normalsize - g \beta \Large\frac{\partial t}{\partial q}\normalsize \, . \quad (7)[/math]
Combining Eqs. (6, 7) gives
[math]2 c \Large\frac{\partial^2 t}{\partial pq}\normalsize = - 3 \Bigg( \Large\frac{\partial c}{\partial p}\normalsize \Large\frac{\partial t}{\partial q}\normalsize + \Large\frac{\partial c}{\partial q}\normalsize \Large\frac{\partial t}{\partial p}\normalsize \Bigg) \,. \qquad (8)[/math]
Solution of the nonlinear wave equations
We change now to two new independent variables [math]\lambda, \sigma[/math] instead of [math]p, q[/math] and [math]x, t[/math],
[math]\lambda = p-q = 2 (u+g \beta t)\, , \; \sigma = p+q = 4 c = 4 \sqrt{g(\eta - \beta x)} \, . \qquad (9)[/math]
The instant shoreline (water line) is given by [math]\sigma = 0[/math]. The variables [math]\sigma, \lambda[/math] depend on the wave shape close to the water line.
Far from the shoreline we have [math]\sigma \approx 4 \sqrt{g \beta |x|}[/math]. After a time [math]g \beta t \gt \gt |u|[/math] we have [math]\lambda \approx 2 g \beta t[/math].
Derivation of Eq. (9) using the chain rule gives
[math]\Large\frac{\partial t}{\partial p}\normalsize = \Large\frac{\partial t}{\partial \lambda}\normalsize +\Large\frac{\partial t}{\partial \sigma}\normalsize \, , \; \Large\frac{\partial t}{\partial q}\normalsize = - \Large\frac{\partial t}{\partial \lambda}\normalsize + \Large\frac{\partial t}{\partial \sigma}\normalsize \, . \qquad (10)[/math]
Substitution in Eq. (8) gives
[math]\sigma \Bigg( \Large\frac{\partial^2 t}{\partial \lambda^2}\normalsize - \Large\frac{\partial^2 t}{\partial \sigma^2}\normalsize \Bigg) – 3 \Large\frac{\partial t}{\partial \sigma}\normalsize =0 \, . \qquad (11)[/math]
Because [math]g \beta t = - u + \lambda / 2[/math], Eq. (11) also holds for the velocity [math]u(\sigma, \lambda)[/math]. A solution of Eq. (11) can be found when writing the velocity in the form
[math]u(\sigma, \lambda) \equiv \Large\frac{1}{\sigma}\frac{\partial \phi(\sigma,\lambda)}{\partial \sigma}\normalsize \, . \qquad (12)[/math]
Substitution of this expression for [math]t[/math] in Eq. (11) gives
[math] \Large\frac{\partial}{\partial \sigma}\normalsize \Big( \sigma \Large\frac{\partial \phi}{\partial \sigma}\normalsize \Big) - \sigma \Large\frac{\partial^2 \phi}{\partial \lambda^2}\normalsize =0 \, . \qquad (13)[/math]
It can easily be verified that a solution of this equation is given by
[math]\phi (\lambda, \sigma) = A \, J_0( \chi \sigma) \, \cos (\chi \lambda -\psi) \, , \qquad (14)[/math]
where [math]A, \chi, \psi[/math] are arbitrary constants and [math]J_0[/math] is a Bessel function of the first kind. This is not a simple expression because [math]\lambda[/math] and [math]\sigma[/math] depend on the solution [math]u, \eta \,[/math] according to Eq. (9).
Boundary conditions
The solution is further defined by the initial ([math]t=0[/math]) wave surface elevation [math]\eta(x,0)[/math] from the instant shoreline [math]\sigma =0[/math] to [math]\sigma = \infty[/math]. The fluid is assumed to be initially at rest: [math]\lambda=0, \; u=0[/math]. As the wave motion is assumed frictionless, no boundary forcing is needed to keep the wave motion going. However, if the initial surface oscillation does not extend to infinity, the wave motion near the shoreline will eventually come to rest.
From the initial wave surface elevation it is possible to compute the derivative [math]\partial u / \partial \lambda \equiv f(\sigma)[/math] at [math]\lambda=0[/math]. First the derivative [math]\partial x / \partial \sigma[/math] has to be determined. This can be done by solving Eq. (9) at [math]t = 0[/math] to determine the function [math]x(\sigma, \lambda=0)[/math] and the derivative [math]\partial x / \partial \sigma[/math]. The equation [math]\; \sigma = 4 \sqrt{g(\eta(x,0) - \beta x)} [/math] can for some particular functions [math]\eta(x,0)[/math] be solved analytically, but in general only a numerical solution can be obtained.
Using successively Eqs. (9, 4, 5, 10) and [math]u=0[/math] we have
[math]\Large\frac{\partial x}{\partial \sigma}\normalsize = \Large\frac{\partial x}{\partial p} \frac{\partial p}{\partial \sigma}\normalsize + \Large\frac{\partial x}{\partial q}\frac{\partial q}{\partial \sigma}\normalsize = \large\frac{1}{2}\normalsize \Big( \Large\frac{\partial x}{\partial p}\normalsize + \Large\frac{\partial x}{\partial q}\normalsize \Big) = \large\frac{1}{2} c \, \Big( - \Large\frac{\partial t}{\partial p}\normalsize + \Large\frac{\partial t}{\partial q}\normalsize \Big) = - c \Large\frac{\partial t}{\partial \lambda}\normalsize . [/math]
From Eq. (9) we have [math]f(\sigma) \equiv \Large\frac{\partial u}{\partial \lambda}\normalsize = \large\frac{1}{2}\normalsize – g \beta \Large\frac{\partial t}{\partial \lambda}\normalsize = \large\frac{1}{2}\normalsize + \Large\frac{4 g \beta}{\sigma}\frac{\partial x}{\partial \sigma}\normalsize \, . \qquad (15) [/math]
Carrier and Greenspan (1957[1]) derived the following expression relating the velocity field [math]u(\sigma, \lambda)[/math] to the initial condition [math]\partial u / \partial \lambda \equiv f(\sigma)[/math] at [math]\lambda=0[/math]:
[math]u (\sigma, \lambda) = \Large\frac{1}{\sigma}\normalsize \int_0^{\infty} d\chi J_1(\chi \sigma) \sin \chi \lambda \int_0^{\infty} d\sigma' \sigma'^2 J_1(\chi \sigma') f(\sigma') \, , \qquad (16) [/math]
where [math]J_1[/math] is a Bessel function of the first kind.
The potential [math]\phi[/math] (Eq. (12)) is given by
[math]\phi (\sigma, \lambda) = - \int_0^{\infty} d\chi J_0(\chi \sigma) \Large\frac{\sin \chi \lambda }{\chi}\normalsize \int_0^{\infty} d\sigma' \sigma'^2 J_1(\chi \sigma') f(\sigma') \, . \qquad (17) [/math]
Using Eqs. (4, 5, 9) we find for [math]t \gt 0[/math]
[math]\Large\frac{\partial x}{\partial \sigma}\normalsize = u \,\Large\frac{\partial t}{\partial \sigma}\normalsize - c \, \Large\frac{\partial t}{\partial \lambda}\normalsize = \Large\frac{1}{g \beta}\normalsize \Bigg( - u \, \Large\frac{\partial u}{\partial \sigma}\normalsize - \Large\frac{1}{8}\normalsize \sigma + \Large\frac{1}{8}\frac{\partial^2 \phi}{\partial \lambda \partial \sigma}\normalsize \Bigg) \, . [/math]
The wave elevation [math]\eta[/math] and the coordinates [math]x, t[/math] can now determined from
[math]x = \Large\frac{1}{g \beta}\normalsize \Bigg( -\large\frac{1}{2}\normalsize u^2 - \large\frac{1}{16}\normalsize \sigma^2 + \large\frac{1}{4}\Large\frac{\partial \phi}{\partial \lambda}\normalsize \Bigg) \, , \qquad (18)[/math]
[math]t = \Large\frac{1}{2 g \beta}\normalsize ( \lambda – 2 u ) \, , \qquad (19)[/math]
[math]\eta = \Large\frac{c^2}{g}\normalsize + \beta x = \Large\frac{1}{g}\normalsize \Bigg( -\large\frac{1}{2}\normalsize u^2 + \large\frac{1}{4}\Large\frac{\partial \phi}{\partial \lambda}\normalsize \Bigg) \, . \qquad (20)[/math]
From a few examples with initial wave shapes that allow an analytical solution of the equations (15) and (16), Carrier and Greenspan (1957[1]) showed that the wave run-up at the shoreline is higher than the maximum initial wave amplitude.
The wave amplitude given by equations (17) and (20) vanishes at large distances from the shoreline. Due to the uniform slope of the bed, there is no limit to the depth increase, which is physically unrealistic. The practical relevance of the theory is therefore limited to a region close to the shoreline. At larger distances, a wave boundary condition must be applied. The mathematical treatment of the wave boundary condition for the nonlinear problem is very complex (see, for example, Rybkin et al. (2021[2]). However, useful expressions can be obtained in the linear case discussed below.
Linear wave equations
The linear wave equations read
[math]\Large\frac{\partial \eta}{\partial t}\normalsize + \Large\frac{\partial (hu)}{\partial x}\normalsize = 0 \; , \quad \Large\frac{\partial u}{\partial t}\normalsize + g \Large\frac{\partial \eta}{\partial x}\normalsize = 0\, . \qquad (21)[/math]
The solution of these equations can be found with a similar transformation of the independent variables as for the nonlinear case, but retaining only the first order linear terms,[3]
[math]\lambda_0 = 2 g \beta t \, , \; \sigma_0 = 4 c = 4 \sqrt{- g \beta x} \, . \qquad (22)[/math]
The old variables are now related to the new variables by the expressions
[math]\eta = \Large\frac{1}{4g}\frac{\partial \phi_0}{\partial \lambda_0}\normalsize \, , \quad x = - \Large\frac{\sigma_0^2 }{16 g \beta}\normalsize \, , \quad t = \Large\frac{\lambda_0}{2 g \beta}\normalsize \, .\qquad (23)[/math]
The wave orbital velocity is related to the velocity potential [math]\phi_0[/math] according to equation (12),
[math]u(\sigma_0, \lambda_0) = \Large\frac{1}{\sigma_0}\frac{\partial \phi_0(\sigma_0,\lambda_0)}{\partial \sigma_0}\normalsize \, , \qquad (24)[/math]
which satisfies the linear differential equation (11),
[math] \Large\frac{\partial}{\partial \sigma_0}\normalsize \Big( \sigma_0 \Large\frac{\partial \phi_0}{\partial \sigma_0}\normalsize \Big) - \sigma_0 \Large\frac{\partial^2 \phi_0}{\partial \lambda_0^2}\normalsize =0 \, . \qquad (25)[/math]
It can easily be verified that the expressions (23-25) solve the linear equations (21). The solution is the same expression (14) as for the nonlinear case,
[math]\phi_0 (\lambda_0, \sigma_0) = A_0 \, J_0( \chi \sigma_0) \, \cos (\chi \lambda_0 -\psi) \, . \qquad (26)[/math]
The linear solution can be readily expressed as a function of the original variables [math]x, t[/math], for arbitrary [math]A_0, \psi[/math]. Considering a standing sinusoidal wave with angular frequency [math]\omega = 2 \pi /T[/math], we have
[math]\eta(x,t) = \Large\frac{1}{4 g}\frac{\partial \phi_0}{\partial \lambda_0}\normalsize = \eta_{max} \, J_0( \large\frac{2 \omega}{g \beta}\normalsize \sqrt{-g \beta x}) \, \sin (\omega t -\psi) \, , \quad u(x,t) = \Large\frac{1}{\sigma_0}\frac{\partial \phi_0}{\partial \sigma_0}\normalsize = \Large\frac{g \eta_{max}}{\sqrt{-g \beta x}}\normalsize J_1( \large\frac{2 \omega}{g \beta}\normalsize \sqrt{-g \beta x}) \, \cos (\omega t -\psi) \,. \qquad (26)[/math]
The solution for the linear and nonlinear cases are identical for large values of [math]x[/math] and [math]t[/math]. In the linear case, the solution is restricted to [math]x \lt 0[/math]. At [math]x=0[/math], the maximum height [math]\eta_{max}[/math] of the linear wave equals the maximum height of the nonlinear wave (same initial conditions) at the shoreline [math]\sigma=0[/math] [3]. For the linear case, [math]\eta_{max}[/math] equals the run-up [math]R[/math] and the maximum shoreline advance [math]x_R[/math] can thus be determined by [math]x_R = \eta_{max} / \beta[/math].
In real situations, at some distance from the shoreline the bed slope will decrease and eventually become very small. In the case a boundary condition must be applied at the seaward boundary of the sloping nearshore zone. Let [math]h_0 = -\beta x_0[/math] be the depth of the offshore area and let [math]H_0[/math] be the wave height at the boundary [math]x = -x_0[/math]. If [math]y = \large\frac{2 \omega}{g \beta}\normalsize \sqrt{g h_0} \gt \gt 1[/math], the Bessel function can be approximated by [math]J_0(y) \approx \sqrt{\large\frac{2}{\pi y}\normalsize} \cos(y - \large\frac{\pi}{4}\normalsize) .[/math] Substitution in the expression (26) gives
[math]R = \eta_{max} = H_0 \Big( \Large\frac{\pi}{4 \beta}\normalsize \Big)^{1/2} \Big( \Large\frac{h_0 \omega^2}{g}\normalsize \Big)^{1/4} \, . \qquad (27)[/math]
Wave breaking
The transformation of [math]x, t [/math] to [math]\sigma, \lambda[/math] variables must be single-valued, which is equivalent to the condition that no wave breaking will occur[1]. This is the case if the Jacobian [math]|J| = \Large\frac{\partial x}{\partial \sigma}\frac{\partial t}{\partial \lambda}\normalsize - \Large\frac{\partial t}{\partial \sigma}\frac{\partial x}{\partial \lambda}\normalsize = \large\frac{\sigma}{4}\normalsize \Bigg| \big( \Large\frac{\partial u}{\partial \sigma}\normalsize \big)^2 - \big( \large\frac{1}{2}\normalsize - \Large\frac{\partial u}{\partial \lambda}\normalsize \big)^2 \Bigg| \neq 0[/math].
For the linear case, Eq.(26), this condition is met if the maximum run-up (height at the shoreline) [math]\quad \eta_{max} \lt \eta_{max}^{br} = \Large\frac{g \beta^2}{2 \omega^2}\normalsize \, . \qquad (28)[/math]
This condition can be related to the offshore wave height [math]H_0[/math] by using the expression (27),
[math]H_0 \lt H_0^{br} = h_0 \pi^{-1/2} \Big( \Large\frac{g \beta^2}{h_0 \omega^2}\normalsize \Big)^{5/4} \, . \qquad (29)[/math]
This condition implies that short waves (period [math]T =2 \pi / t \sim 10 \, s[/math]) may break on sandy beaches ([math]\beta \sim 0.05[/math]) if offshore wave heights are larger than a centimeter. For wave heights on the order of 1 m, non-breaking conditions may occur for infragravity waves ([math]T \gt 60 \, s[/math]) on sandy beaches ([math]\beta \sim 0.05[/math]) or for short waves ([math]T \sim 10 \, s[/math]) on steep slopes ([math]\beta \gt 1/3[/math]).
The condition (29) can be compared to the criterion of no breaking for the surf similarity parameter according to Battjes (1974[4]),
[math]\xi \gt \xi_{br} = \beta \Big( \Large\frac{L_0}{H_{br}}\normalsize \Big)^{1/2} =(2 \pi g)^{1/2} \beta \omega^{-1} H_{br}^{-1/2} \approx 3.3 \, . \qquad (30)[/math]
According to this criterion, short waves (period [math]T \sim 10 \, s[/math]) may break on sandy beaches ([math]\beta \sim 0.05[/math]) if offshore wave heights are larger than a few centimeters. The condition (29) is thus more severe than the criterion (30), which has been tested in numerous field and lab experiments.
Related articles
References
- ↑ 1.0 1.1 1.2 1.3 Carrier, G. F. and Greenspan, H. P. 1958. Water waves of finite amplitude on a sloping beach. Jour. Fluid Mech. 4: 97-109
- ↑ Rybkin, A., Nicolsky, D., Pelinovsky, E. and Buckel, M. 2021. The Generalized Carrier–Greenspan Transform for the Shallow Water System with Arbitrary Initial and Boundary Conditions. Water Waves 3: 267–296
- ↑ 3.0 3.1 Massel, S.R. and Pelinovski, E.N. 2001. Run-up of dispersive and breaking waves on beaches. Oceanologia 43: 61-97
- ↑ Battjes, J.A. 1974. Surf similarity. Proceedings 14th International Conference on Coastal Engineering, pp. 466–480
Please note that others may also have edited the contents of this article.
|