Infragravity waves

From Coastal Wiki
Revision as of 12:39, 5 June 2024 by Dronkers J (talk | contribs)
Jump to: navigation, search


Introduction

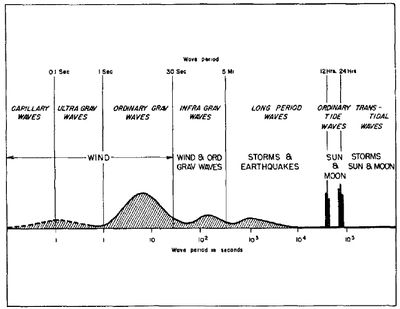
Figure 1: Classification of ocean waves according to wave period. The forces responsible for various portions of the spectrum are shown. The relative amplitude is indicated by the curve. From Munk [1]

Infragravity waves are ocean surface waves with a typical period of 25-250s (frequency of 0.004-0.04 Hz, see Fig. 1). They are indirectly formed by the wind because they receive their energy from the short sea- and swell waves, which have typical periods of 2-20s. While infragravity waves are generally small on the open ocean, close to the coast they can be up to a few meters in height and thus dominate the water motion, in particular during storms. Since their first observations their presence has been observed to influence many nearshore processes[2][3] varying from coastal erosion during storms, to coral reef hydrodynamics and the generation of seiche in harbors. Their generation and transformation while travelling towards the coast will be described in more detail below, together with a brief description of their noted influence in various coastal environments.


Generation

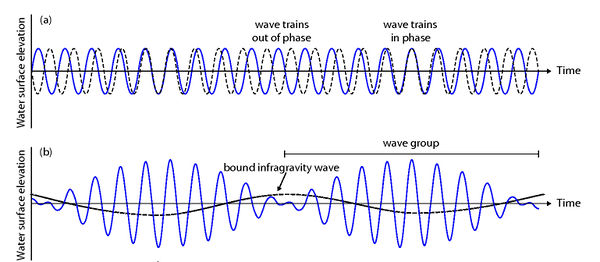
Infragravity waves are indirectly formed by the wind. Their creation is linked to the presence of short-wave groups, which are formed due to the superposition of short-wave trains, with slightly different wave lengths and frequencies. When the waves are in phase their amplitudes are added, and when they are out of phase their amplitudes damp each other out (Fig. 2a). This results in a wave group structure (Fig. 2b), which is irregular in shape due to the various frequencies present in a natural wave field. The first mechanism that can form infragravity waves is due to the fact that the larger short waves in the short-wave group transport more momentum than the smaller waves, leading to a water level lowering under the larger waves, and a relative water level increase under the smaller waves. This induces a variation of the mean water level on a group scale, and results in energy that fluctuates at the same frequency as the wave group. This induced wave is bound to the group, and is 180 degrees out of phase. A mathematical derivation is given in the appendix. On the open sea/ocean these bound infragravity waves are only about a centimeter in height[4].


Figure 2a. The merging of two wave trains of slightly different wave lengths, but the same amplitude. Figure 2b. The two wave trains form wave groups and induce a long bound wave. Modified from Open University[5].


The second mechanism in which infragravity waves are formed is related to the varying breakpoint of the short-wave group in shallow water[6]. The largest short waves in the group will break slightly further offshore than the smallest waves in the group. This forces a time-variation of the radiation stress in the surf zone, which is balanced by a time-varying wave setup, and creates energy at infragravity frequencies. Battjes et al. [7] suggested that the importance of the two above mentioned mechanisms varies with beach slope. The bound wave mechanism is strongest on gently sloping beaches whereas the breakpoint mechanism dominates on steep beaches.

A third mechanism that can enhance water motions with infragravity periods is the merging of wave bores in the surf zone. Wave bores that have formed after wave breaking propagate faster onshore when they ride on the crest of an infragravity wave and slower when they ride on the trough. Fast propagating bores will grow by overtaking slower ones and thus transfer short wave energy to water motions at longer periods. This process is frequently observed on gently sloping beaches, but seems to be a less dominant mechanism for infragravity wave generation[8].

Propagation

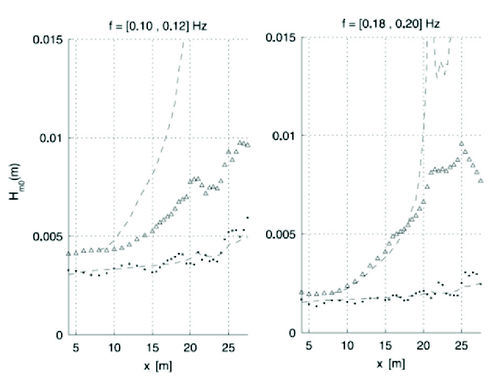
Figure 3: Significant wave height [math]H_{m0}[/math] values of incoming (triangles) and outgoing (dots) infragravity waves for different frequency bands propagating over a 1:70 sloping laboratory bed. Lower dashed curve: Green ([math]H \approx h^{-1/4}[/math]), fitted to outgoing wave heights in the zone offshore from [math]x[/math] = 20 m (offshore boundary at [math]x[/math] = 0). Upper dashed curve: LHS62 asymptote ([math]H \approx h^{-5/2}[/math]), initiated with wave height at [math]x[/math] = 8 m. Modified from Battjes et al[7].

The bound infragravity wave generated on the open ocean grows slowly but steadily while travelling into shallower water. In addition to conservative shoaling they grow due to a continuous nonlinear energy transfer from the short waves. In shallow water, when the energy transfers strengthen due to near-resonance conditions, the infragravity wave grows in height more rapidly. The maximum height that the infragravity wave can obtain depends on the bed slope, as during the longer propagation time in shallow water on a gentle slope, more energy can be transferred than on a steep slope[9]. The growth rate of infragravity waves varies depending on the typical frequency, from the free-wave variation [math]h^{-1/4}[/math] (Greens law, [math]h[/math] is water depth) for the lower frequencies, to nearly the shallow water limit of the equilibrium solution [math]h^{-5/2}[/math] (LHS62 asymptote [10]) for the higher frequencies, see also Fig. 3. In the surf zone, where the short waves are breaking, the group structure disappears, and the infragravity waves propagate ashore as free waves[10][11][12].


Edge waves

Infragravity waves that arrive at the coast are generally reflected off the beach and, depending on bathymetry and angle of propagation, can travel back into the open sea as leaky waves or become trapped to the coast as edge waves. Edge waves remain close to the coast by repetitive refraction over a sloping bathymetry followed by reflection off the beach. Edge waves are standing in the cross-shore direction and are progressive alongshore, with their maximum amplitude at the shoreline. Their shapes are characterised by edge modal numbers [math]n[/math], that correspond to the number of zero-crossings in the cross-shore before being refracted. Mode 0 is the most common and has the smallest alongshore wave length. The largest part of reflected infragravity waves on gently sloping beaches is assumed to become an edge wave[13]. Approximately shorenormal waves result in an equal distribution of infragravity edge waves along the coast, but with obliquely incident waves and the breaking-induced alongshore current an asymmetric distribution in dominant propagation direction is created. The presence of a sandbar may cause infragravity waves to become trapped on the bar, refracting from one side to the other side of the bar[14].


Dissipation

During the decades after their first observations it was assumed that, contrary to the incident short waves that break and dissipate their energy close to shore, infragravity waves reflect off the beach face and conserve their energy completely due to their low steepness (long wave length and relatively low wave height). Nowadays, it is well established that close to the shoreline infragravity waves can lose a substantial part of their energy too [15][16][17]. Infragravity waves are assumed to dissipate their energy by transferring their energy back to higher frequencies by the development of higher harmonics[17][18][19]. On gently sloping beaches, the infragravity waves with the highest frequencies are steepened, with the waveform changing to skewed (peak wave peaks and longer wave troughs) and asymmetric (sawtooth shape). These steep infragravity waves evolve into bores and dissipate their energy by breaking near the shoreline[20][21].

Bottom friction is only of secondary importance for energy dissipation on sandy beaches, but highly relevant on coral reefs, where the friction factor is an order of magnitude larger[22][23].

The relative importance of reflection versus dissipation depends on the beach slope. On gently sloping beaches where infragravity waves are relatively large compared to the incident short waves, infragravity waves generate higher harmonics and steepen up, leading to breaking and associated large energy losses close to the shoreline. On the contrary, on steep sloping beaches infragravity waves are relatively small and interact with the short-wave spectral peak during energy loss. Energy is spread to a large range of higher (short-wave) frequencies, but overall less energy is removed from the infragravity band than on more gentle slopes. According to field experiments[24][25] the transition between steep slope and mild slope regimes occurs for values of the normalized bed slope parameter [math]\beta_H[/math] around 3, where [math]\beta_H= \Large\frac{h_x}{\omega} \sqrt{\frac{g}{H}} ,[/math] and [math]h_x=[/math]beach slope, [math]\omega=[/math]angular frequency, [math]g=[/math]gravitational acceleration and [math]H=[/math]height of the incoming infragravity wave.


Impact on various coastal environments

Beaches

Hydrodynamics

The hydrodynamics close to the coast are affected by infragravity waves in various ways. Infragravity waves contribute to the run-up on (especially gently sloping) beaches [26][27][28][29] and coral reefs[30]. This larger run-up can lead to more overwashing and flooding, and can therefore contribute considerably to beach- and dune- erosion[31]. Many empirical relations have been proposed to relate incident wave conditions to the maximum (infragravity) runup, suggesting proportionality to [math](H_{s0}/L_0)^{1/2}[/math], where [math]H_{s0}[/math] and [math]L_0[/math] are the offshore short waveheight and wave length, respectively[32]. More accurate run-up predictions require taking the directional spread and frequency spread of the wave field into account [33]. Se also Swash zone dynamics.

Observations show that infragravity motions influence the temporal behavior of rip currents [34], stimulating the detaching of eddies from the rip currents and thereby affecting the mixing in the cross- and alongshore[35]. Infragravity waves also induce fluctuations in the groundwater by bottom pressure variations, in particular in the saturated swash zone on sandy, gently sloping beaches with an infragravity- dominated swash zone[36][37].

Sand transport

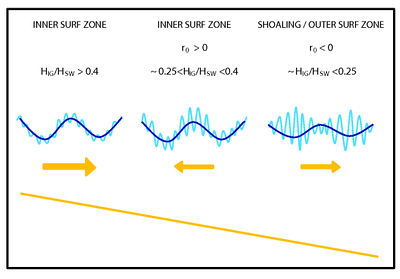
Figure 4: Conceptual figure for sand suspension mechanisms and resulting infragravity-wave flux directions. The magnitude might change with height above the bed, but the direction is expected to be the same. Note that the size of the smallest waves for negative [math]r_{0}[/math] is similar to the largest waves for positive [math]r_{0}[/math]. Modified from De Bakker[38].

Sand suspension and transport by infragravity waves has been investigated by many research groups. The observed suspension mechanisms, transport magnitudes and directions vary substantially between these studies, which seems to be linked to the different ratio of infragravity-wave (IG) height with respect to the short-wave (SW) height [math]H_{IG}/H_{SW}[/math] during the various studies[38] (Fig. 4). When the infragravity wave height is relatively small (generally true for somewhat steeper beaches), sand is suspended by the short waves on infragravity time-scale. When the infragravity wave is still bound, the largest short waves are at the trough of the infragravity wave (negative correlation [math]r_0 [/math] between the short-wave group and the infragravity wave at zero lag). Because most sand is stirred here, bound infragravity waves transport sand seaward. In the inner part of the surf zone, when the infragravity wave is free, the largest short waves are present at the crest of the infragravity wave (the water depth is locally increased here; short waves can prevail a little longer and correlation [math]r_0 \gt 0 [/math]), and sand transport is mostly shoreward directed by the onshore infragravity velocities. Model simulations show that low-sloping beaches promote dune growth via infragravity swash processes even under energetic offshore wave forcing[39]. However, this transport component is in general only a small fraction of the total cross-shore transport. When the infragravity-wave height is relatively large compared to short-wave height (generally true in the inner surf zone on gently sloping beaches), infragravity waves can stir sand up from the bed themselves as well, and sand is suspended under the offshore directed infragravity wave velocities. This process is most likely enhanced by an interplay with the undertow. For these conditions, infragravity-wave transport can contribute considerably to seaward transport, especially during storms when the infragravity wave is most energetic. See also Shoreface profile.

Tidal inlets

At wave-dominated shallow tidal inlets (mean water depth and tidal amplitude of the same order), observations and model simulations show that velocities associated with infragravity frequencies can be of the same order of magnitude, or sometimes even larger, than tidal currents[40] [41]. As infragravity-wave energy is blocked during ebb, due to the opposing tidal currents, infragravity waves propagate only into the inlet and lagoon during rising tide. This could promote a flood dominance, and contribute to a possible closure of shallow inlets during winter storms[40].

Coral reef environments

As short-waves dissipate their energy strongly while travelling over the reef flat, the longer infragravity waves can dominate the water motion more and more further away from the reef edge[23][42]. Infragravity waves are usually progressive over wide reefs with relatively shallow water depths and high roughness values, whereas they can be reflected and resonant on smooth reefs and for certain combinations of water depth and reef width[43][44]. See also Coral reefs.

Seiche in harbors

Resonance of infragravity waves in semi-enclosed basins such as inlets and harbors can seriously affect harbor operations and cause damage to for example moored ships[45][46]. Resonance occurs when the period of the incident long waves is close to the natural oscillation periods of the basin. It causes standing waves to form within the basin with strong vertical water oscillations at the antinodes, and strong horizontal currents at the nodes. Small harbors in particular (1 km[math]^2[/math] and a waterdepth of about 5-10 m) have modes close to the infragravity periods, and are therefore prone to seiche induced by these waves[47]. Seiches occurring in larger harbor basins are primarily caused by subtidal wave motions at periods longer than the infragravity periods; these wave motions (from several minutes up to about 1 hour) are thought to be related to atmospheric pressure fluctuations during storms or to internal wave motions in the ocean[48][49].

Other

In addition, infragravity waves can contribute to the seismic movement of coastal cliffs [50], and are related to the occurrence of microseisms with periods between 30-300 s, also called the Earth’s hum[51][52]. Furthermore, it is suggested that infragravity frequencies also play an important role in ice-shelf collapse[53].


Further reading

A more detailed discussion of the topics introduced in this article is given in:
Bertin, X., de Bakker, A., van Dongeren, A., Coco, G., et al. 2018. Infragravity waves: From driving mechanisms to impacts. Earth-Science Reviews 177: 774–799


Appendix

Here a mathematical derivation is presented of the formation of infragravity waves driven by momentum transfer from alternating large and small waves in the wave group. An irregular wave field (Fig. 2a) can be represented by a superposition of sinusoidal propagating waves with random phases and amplitudes,

[math]\eta (x,t) = \Re \Bigl[\sum_{n=1}^{N} a_n \exp[i (k_n x - \omega_n t) ] \Bigr], \qquad (A1)[/math]

where [math]a_n=|a_n| \exp(i\chi_n)[/math] are complex amplitudes. We will assume that the radial frequencies [math]\omega_n[/math] and wave numbers [math]k_n[/math] of the individual wave components are fairly close to the average wave frequency [math]\omega[/math] and average wave number [math]k[/math]. The individual wave components satisfy the frequency dispersion relation

[math]c_n = \omega_n / k_n, \quad \omega_n = \sqrt{g k_n \tanh k_n h} , \quad c= \omega / k, \quad \omega = \sqrt{g k \tanh kh} , \qquad (A2)[/math]

where [math]c_n[/math] is the propagation speed of the n-th wave component. It is assumed that the spatial variation of the local depth [math]h[/math] is very small over the wave orbital excursion [math]a/(kh)[/math].

The wave field can be written as

[math]\eta = \Re \Bigl[a \exp[i(kx-\omega t)] \Bigr] , \qquad a = \sum_n a_n \exp \Bigl[i \big( (k_n-k)x - (\omega_n -\omega)t \big)\Bigr] , \qquad (A3)[/math]

where [math]|a|[/math] is a slowly varying function representing the envelope of the wave group (Fig. 2b). Because the assumption of a narrow wave spectrum,[10]

[math]\Large\frac{k_n-k}{\omega_n - \omega}\normalsize \approx \Large\frac{d \omega}{dk}\normalsize \equiv c_g = c \, (\Large\frac{1}{2}\normalsize + \Large\frac{2kh}{\sinh (2 kh)}\normalsize ) . \qquad (A4)[/math]

Inserting (A4) in (A3) gives

[math]a = \sum_n a_n \exp[i(k_n-k)(x-c_g t] . \qquad (A5)[/math]

This expression shows that the wave group propagates with the wave speed [math]c_g[/math]. The wave group celerity is typically smaller than the celerity of the individual waves, except in very shallow water ([math]kh \lt \lt 1 [/math]). The wave length of the wave group is therefore much longer than the wave length of the individual wave components.

Because the energy in the wave group has a spatial variation, the gradient of the radiation stress [math]S_{XX}[/math] is non zero and varies at the same frequency as the wave group. This spatial variation of the radiation stress drives a spatial variation in the mean water level [math]\overline{\eta}[/math] (averaged over the individual waves) and in the associated mass transport [math]q = (h + \overline{\eta}) \overline{u}[/math]. The variation in mean water level is typically much smaller than the wave amplitude [math]|a|[/math] and the depth [math]h[/math]. The mean water level and mass transport therefore satisfy approximately the relations

Continuity equation: [math]\quad \Large\frac{\partial q}{\partial x}\normalsize + \Large\frac{\partial \overline{\eta}}{\partial t}\normalsize =0 , \qquad (A6)[/math]

Momentum balance equation (see Shallow-water wave theory, Eq. 3.25): [math]\quad \Large\frac{\partial q}{\partial t}\normalsize + \Large\frac{1}{\rho}\frac{\partial S_{XX}}{\partial x}\normalsize = - gh \Large\frac{\partial \overline{\eta}}{\partial x}\normalsize , \qquad (A7) [/math]

where the radiation stress [math]S_{XX}[/math] is given by (see Shallow-water wave theory, Eq. (3.26 and (3.30 )):

[math]S_{XX} =\overline{\int _{-h}^{\eta } (p+\rho u^{2} )dz } - \int _{-h}^{\overline{\eta}} p_0 dz \approx \Large\frac{1}{2}\normalsize \rho g |a|^2 \left(\Large\frac{2kh}{\sinh 2kh}\normalsize +\Large\frac{1}{2}\normalsize \right) . \qquad (A8)[/math]

The latter approximate equality holds for linear Airy waves.

Because the wave group moves with celerity [math]c_g[/math], the time derivates in Eqs. (A6) and (A7) can be replaced by spatial derivatives, [math]\Large\frac{\partial}{\partial t}\normalsize \approx - c_g \Large\frac{\partial}{\partial x}\normalsize , [/math] giving[10]:

[math]\Large\frac{\partial q}{\partial x}\normalsize = c_g \Large\frac{\partial \overline{\eta}}{\partial x}\normalsize , \qquad c_g \Large\frac{\partial q}{\partial x}\normalsize + \Large\frac{1}{\rho}\frac{\partial S_{XX}}{\partial x}\normalsize = - gh \Large\frac{\partial \overline{\eta}}{\partial x}\normalsize . \qquad (A9) [/math]

The equations (A9) are linear differential equations in the variable [math]x[/math] which can be integrated, with the result[10]:

[math] \overline{\eta} = - \Large\frac{S_{XX}}{\rho (gh - c_g)}\normalsize , \qquad q = - \Large\frac{c_g S_{XX}}{gh - c_g}\normalsize . \qquad (A10)[/math]

The first expression in (A10) shows that the mean water level is depressed where [math]S_{XX}[/math] is large, thus in the wave group where the amplitudes are large, and is lifted where the amplitudes in the wave group are small, see Fig, 2b. This variation of the mean water level in the wave group represents a bound infragravity wave, with phase opposite to the wave group envelope.

The second expression in (A10) shows that the bound infragravity wave reduces the onshore wave orbital motion of the largest waves in the wave group. Therefore it favors offshore sediment transport compared to onshore transport.


References

  1. ↑ Munk, W., 1950. Origin and generation of waves, in: Proceedings of First Conference on Coastal Engineering, Long Beach, California
  2. ↑ Munk, W., 1949. Surf beat, in: Eos Trans. AGU, 30, 849-854
  3. ↑ Tucker, M., 1950. Surfbeats: Sea waves of 1 to 5 minutes period., in: Proc. R.Soc. London A278 202-565-573
  4. ↑ Aucan, J., Ardhuin, F., 2013. Infragravity waves in the deep ocean: An upward revision. Geophysical Research Letters 40, 3435–3439
  5. ↑ OpenUniversity, 1994. Waves, Tides and Shallow-water Processes. Pergamon Press, Oxford
  6. ↑ Symonds, G., Huntley, D., Bowen, A.J., 1982. Two-dimensional surf beat: Long wave generation by a time-varying breakpoint. Journal of Geophysical Research 87, 492–498
  7. ↑ 7.0 7.1 Battjes, J.A., Bakkenes, H.J., Janssen, T.T., van Dongeren, A.R., 2004. Shoaling of subharmonic gravity waves. Journal of Geophysical Research 109. C02009, doi:10.1029/2003JC001863
  8. ↑ Tissier, M., Bonneton, P., Ruessink, B., 2017. Infragravity waves and bore merging. In: Proceedings of the Conference Coastal Dynamics 2017. ASCE, Helsingør, Denmark, pp. 451–460
  9. ↑ De Bakker, A.T.M., Tissier, M.F.S., Ruessink, B.G., 2015. Beach steepness effects on nonlinear infragravity-wave interactions: a numerical study. Journal of Geophysical Research 121, doi:10.1002/2015JC011268
  10. ↑ 10.0 10.1 10.2 10.3 10.4 Longuet-Higgins, M.S., Stewart, R.W., 1962. Radiation stress and mass transport in gravity waves, with application to ’surf beats’. Journal of Fluid Mechanics 13, 481–504
  11. ↑ Herbers, T.H.C., Elgar, S., Guza, R.T., 1995. Generation and propagation of infragravity waves. Journal of Geophysical Research 100, 24863–24872
  12. ↑ Ruessink, B.G., 1998. Bound and free infragravity waves in the nearshore zone under breaking and nonbreaking conditions. Journal of Geophysical Research 103, 12.795–12.805
  13. ↑ Herbers, T.H.C., Elgar, S., Guza, R.T., O’Reilly, W.C., 1995b. Infragravity-frequency (0.005-0.05 hz) motions on the shelf. part ii: Free waves. Journal of Physical Oceanography 25, 1063–1079
  14. ↑ Bryan, K., Howd, P., Bowen, A., 1998. Field observations of bar-trapped edge waves. Journal of Geophysical Research: Oceans 103, 1285–1305
  15. ↑ Ruessink, B.G., 1998b. The temporal and spatial variability of infragravity energy in a barred nearshore zone. Continental Shelf Research 18, 585–605
  16. ↑ Sheremet, A., Guza, R.T., Elgar, S., Herbers, T.H.C., 2002. Observations of nearshore infragravity waves: Seaward and shoreward propagating components. Journal of Geophysical Research 107. C8
  17. ↑ 17.0 17.1 Henderson, S.M., Guza, R.T., Elgar, S., Herbers, T.H.C., Bowen, A.J., 2006. Nonlinear generation and loss of infragravity wave energy. Journal of Geophysical Research 111, C12007
  18. ↑ Thomson, J., Elgar, S., Raubenheimer, B., Herbers, T.H.C., Guza, R.T., 2006. Tidal modulation of infragravity waves via nonlinear energy losses in the surfzone. Geophysical Research Letters 33. L05601
  19. ↑ Ruju, A., Lara, J.L., Losada, I.J., 2012. Radiation stress and low-frequency energy balance within the surf zone: A numerical approach. Coastal Engineering 68, 44–55
  20. ↑ Van Dongeren, A., Battjes, J., Janssen, T., van Noorloos, J., Steenhauer, K., Steenbergen, G., Reniers, A., 2007. Shoaling and shoreline dissipation of low-frequency waves. Journal of Geophysical Research 112. C02011
  21. ↑ De Bakker, A.T.M., Herbers, T.H.C., Smit, P.B., Tissier, M.F.S., Ruessink, B.G., 2015. Nonlinear infragravity-wave interactions on a gently sloping laboratory beach. Journal of Physical Oceanography 45, 589–605, doi: 10.1175/JPO–D–14–0186.1
  22. ↑ Pomeroy, A., Lowe, R., Symonds, G., Van Dongeren, A., Moore, C., 2012. The dynamics of infragravity wave transformation over a fringing reef. Journal of Geophyiscal Research 117
  23. ↑ 23.0 23.1 Van Dongeren, A.R., Lowe, R., Pomeroy, A., Trang, D., Roelvink, D., Symonds, G., Ranasinghe, R., 2013. Numerical modeling of low-frequency wave dynamics over a fringing coral reef. Coastal Engineering 73, 178–190, doi: 10.1016/j.coastaleng.2012.11.004
  24. ↑ De Bakker, A.T.M., Tissier, M.F.S., Ruessink, B.G., 2014. Shoreline dissipation of infragravity waves. Cont. Shelf Res. 72, 73–82.
  25. ↑ Inch, K., Davidson, M., Masselink, G., Russell, P., 2017. Correcting wave reflection estimates in the coastal zone. Coast. Eng. 119, 65–71
  26. ↑ Guza, R.T., Thornton, E.B., Holman, R.A., 1984. Swash on steep and shallow beaches, in: Proceedings of the 19th International Conference on Coastal Engineering, ASCE, 708-723
  27. ↑ Holman, R.A., Sallenger, A.H., 1985. Setup and swash on a natural beach. Journal of Geophysical Research 90, 945–953
  28. ↑ Ruessink, B.G., Houwman, K.T., Hoekstra, P., 1998. The systematic contribution of transporting mechanisms to the cross-shore sediment transport in water depths of 3 to 9 m. Marine Geology 152, 295–324
  29. ↑ Ruggiero, P., Holman, R.A., Beach, R.A., 2004. Wave run-up on a high-energy dissipative beach. Journal of Geophysical Research 109, C06025, doi:10.1029/2003JC002160
  30. ↑ Cheriton, O.M., Storlazzi, C.D., Rosenberger, K.J., 2016. Observations of wave transformation over a fringing coral reef and the importance of low-frequency waves and offshore water levels to runup, overwash, and coastal flooding. Journal of Geophysical Research: Oceans 121, 3121–3140
  31. ↑ Roelvink, D., Reniers, A., van Dongeren, A., van Thiel de Vries, J., McCall, R., Lescinski, J., 2009. Modelling storm impacts on beaches, dunes and barrier islands. Coastal Engineering 56, 1133–1152, doi: 10.1016/j.coastaleng.2009.08.006
  32. ↑ Stockdon, H.F., Holman, R.A., Howd, P.A., Sallenger Jr, A.H., 2006. Empirical parameterization of setup, swash and runup. Coastal Engineering 53, 573-588
  33. ↑ Guza, R.T., Feddersen, F., 2012. Effect of wave frequency and directional spread on shoreline runup. Geophysical Research Letters 39, L11607, doi:10.1029/2012GL051959
  34. ↑ MacMahan, J.H., Reniers, A.J.H.M., Thornton, E.B., Stanton, T.P., 2004. Infragravity rip current pulsations. Journal of Geophysical Research 109
  35. ↑ Reniers, A., MacMahan, J., Thornton, E., Stanton, T., Henriquez, M., Brown, J., Brown, J., Gallagher, E., 2009. Surf zone surface retention on a rip-channeled beach. Journal of Geophysical Research: Oceans 114
  36. ↑ Turner, I.L., Rau, G.C., Austin, M.J. and Andersen, M.S., 2016. Groundwater fluxes and flow paths within coastal barriers: observations from a large-scale laboratory experiment (BARDEX II). Coastal Engineering 113, 104-116
  37. ↑ Sous, D., Petitjean, L., Bouchette, F., Rey, V., Meul´e, S., Sabatier, F., Martins, K., 2016. Field evidence of swash groundwater circulation in the microtidal rousty beach, france. Submitted to Advances in Water Ressources
  38. ↑ 38.0 38.1 De Bakker, A.T.M., Brinkkemper, J.A., van der Steen, F., Tissier, M.F.S., Ruessink, B.G., 2016. Cross-shore sand transport by infragravity waves as a function of beach steepness. Journal of Geophysical Research: Earth Surface in press.
  39. ↑ Cohn, N., Ruggiero, P., Garcia-Medina, G., Anderson, D., Sefarin, K.A., Biel, R., 2019. Environmental and morphologic controls on wave-induced dune response. Geomorphology 329, 108–128
  40. ↑ 40.0 40.1 Bertin, X., Olabarrieta, M., 2016. Relevance of infragravity waves at a wave-dominated inlet. Journal of Geophysical Research
  41. ↑ Williams, M.E., Stacey, M.T., 2016. Tidally discontinuous ocean forcing in bar-built estuaries: The interaction of tides, infragravity motions, and frictional control. Journal of Geophysical Research 121, 571–585
  42. ↑ Pomeroy, A.W.M., Lowe, R.J., Van Dongeren, A.R., Ghisalberti, M., Bodde, W., Roelvink, D., 2015. Spectral wave-driven sediment transport across a fringing reef. Coastal Engineering 98, 78–94, 10.1016/j.coastaleng.2015.01.005
  43. ↑ Cheriton, O.M., Storlazzi, C.D., Rosenberger, K.J., 2016. Observations of wave transformation over a fringing coral reef and the importance of low-frequency waves and offshore water levels to runup, overwash, and coastal flooding. Journal of Geophysical Research: Oceans 121, 3121–3140
  44. ↑ Gawehn, M., van Dongeren, A., van Rooijen, A., Storlazzi, C., Cheriton, O., Reniers, A., 2016. Identification and classification of very low frequency waves on a coral reef flat. Journal of Geophysical Research: Oceans 121, 7560–7574
  45. ↑ Bowers, E.C., 1977. Harbour resonance due to set-down beneath wave groups. Journal of Fluid Mechanics 79 (01), 71–92, doi: 10.1017/S0022112077000044
  46. ↑ Naciri, M., Buchner, B., Bunnik, T., Huijsmans, R., Andrews, J., 2004. Low frequency motions of lng carriers moored in shallow water, in: ASME (Ed.), 23rd International Conference on Offshore Mechanics and Arctic Engineering, pp. 995–1006
  47. ↑ Thotagamuwage, D.T., Pattiaratchi, C.B., 2014. Observations of infragravity period observations in a small marina. Ocean Engineering 88, 435–445
  48. ↑ De Jong, M. P. C., Battjes J. A., 2004. Low frequency sea waves generated by atmospheric convection cells, J. Geophysical Res.109, C01011:1-18
  49. ↑ Giese, G.S., Chapman, D.C., 1993. Coastal Seiches. WHOI magazine Oceanus 36(1),38-46
  50. ↑ Young, A.P., Guza, R.T., O’Reilly, W.C., Burvingt, O., Flick, R.E., 2016. Observations of coastal cliff base waves, sand levels, and cliff top shaking. Earth Surface Processes and Landforms 41,15641573
  51. ↑ Nishida, K., 2013. Earth’s background free oscillations. Annual Review of Earth and Planetary Sciences 41, 719–740
  52. ↑ Ardhuin, F., Gualtieri, L., Stutzman, E., 2015. How ocean waves rock the earth: Two mechanisms explain microseisms with periods 3 to 300 s. Geophysical Research Letters 42
  53. ↑ Bromirski, P.D., Diez, A., Gerstoft, P., Stephen, R.A., Bolmer, T., Wiens, D.A., Aster, R.C., Nyblade, A., 2015. Ross ice shelf vibrations. Geophysical Research Letters 42, 7589–7597


The main author of this article is Anouk de Bakker
Please note that others may also have edited the contents of this article.
Citation: Anouk de Bakker (2024): Infragravity waves. Available from http://www.coastalwiki.org/wiki/Infragravity_waves [accessed on 23-11-2024]




References


The main author of this article is Anouk de Bakker
Please note that others may also have edited the contents of this article.
Citation: Anouk de Bakker (2024): Infragravity waves. Available from http://www.coastalwiki.org/wiki/Infragravity_waves [accessed on 23-11-2024]
Retrieved from "https://www.coastalwiki.org/w/index.php?title=Infragravity_waves&oldid=81033"