Difference between revisions of "Closure depth"
Dronkers J (talk | contribs) |
Dronkers J (talk | contribs) |
||
| Line 98: | Line 98: | ||
<math>U_{b}^2 \approx 0.03 \, (s-1) g \, h_{in} . \qquad (A2)</math> | <math>U_{b}^2 \approx 0.03 \, (s-1) g \, h_{in} . \qquad (A2)</math> | ||
| − | The wave orbital velocity <math>U_b</math> can be expressed as a function of the closure depth <math>h_{in}</math> by using linear wave theory and the assumption of negligible energy loss on the lower shoreface, <math>c_g \, E = c_{0g} E_0</math>, where <math>c_g</math> is the wave group velocity, <math>E= 1 | + | The wave orbital velocity <math>U_b</math> can be expressed as a function of the closure depth <math>h_{in}</math> by using linear wave theory and the assumption of negligible energy loss on the lower shoreface, <math>c_g \, E = c_{0g} E_0</math>, where <math>c_g</math> is the wave group velocity, <math>E= \frac{1}{8} g \rho H^2</math> the wave energy at the closure depth and where offshore deep water is indicated by the subscript <math>0</math> – see [[Shallow-water wave theory]] for explanations. Equation (A1) can then be solved numerically. The solution for the inner closure depth can be approximated by the explicit expression (1). A remarkable feature is that this expression does not depend on the grain size <math>d_{50}</math>. In fact, Hallermeier noted that the formula for the closure depth gave the most accurate predictions for small grain sizes, which are normally found on the lower shoreface, seaward of the closure depth. |
Hallermeier based his expression for the outer closure depth <math>h_{out}</math> on the condition that no wave-induced sediment transport occurs at this depth. The critical value of the mobility parameter found from the flume experiments was | Hallermeier based his expression for the outer closure depth <math>h_{out}</math> on the condition that no wave-induced sediment transport occurs at this depth. The critical value of the mobility parameter found from the flume experiments was | ||
Revision as of 17:27, 7 February 2022
Definition of Closure depth:
The inner depth of closure (DoC) marks the transition from upper to lower shoreface, corresponding to the most landward depth seaward of which there is no significant change in bottom elevation during a given time interval[1].
The outer depth of closure marks the transition from lower shoreface to continental shelf, and corresponds to the depth where the influence of wave action on cross-shore sediment transport is on average insignificant compared to other influences. This is the common definition for Closure depth, other definitions can be discussed in the article
|
The definition of the inner depth of closure given by Krauss et al. (1998)[1] is general in that it applies to the open coast where nearshore waves and wave induced currents are the dominant sediment-transporting mechanisms, as well as to non-wave dominated locations, such as the beach adjacent to a long jetty, at which sediment may be jetted offshore by a-large rip current or an ebb tidal shoal where the tidal current is a major contributor to the sediment-transporting processes.
Contents
Relevance of the closure depth concept
Sand transport in the coastal zone is mainly driven by waves. However, this only holds within a zone of limited cross-shore width. In deep water, waves and seabed hardly interact, because wave orbital motion decreases exponentially with depth (see Shallow-water wave theory). The strip along the coast where sand transport is mainly driven by waves is called the active coastal zone. The closure depth indicates the seaward boundary of the active coastal zone. Wave-induced sand transport has both a longshore and a cross-shore component. The longshore component plays a major role in structural long-term shore accretion (transport convergence) or shore erosion (transport divergence). The cross-shore component is mainly responsible for large seasonal sand transfers up and down the beach, especially by alternating mild weather and storm weather conditions (see Fig. 1).
The active coastal zone is a zone of intense morphodynamics: the mutual interaction between wave dynamics and seabed/beach morphology. The influence of nearshore interventions that influence the wave climate (e.g. jetties, groynes, breakwaters, dredging, dumping) will trigger a morphodynamic feedback that extends from the beach to the closure depth. This also holds for the impact of sea level rise. Morphodynamic feedbacks are at the core of the concept of equilibrium shoreface profile. At the annual-decadal time scale (scale of alternating storm and mild weather conditions) morphodynamic activity involves mainly the upper shoreface, the zone of wave transformation, refraction and breaking. At the decadal-centennial time scale sediment exchange between the upper and lower shoreface cannot be ignored. The concept of active coastal zone therefore has a temporal component; the closure depth at shorter timescales is smaller than the closure depth at longer time scales. The shorter timescale and smaller closure depth are most relevant for estimating the impact of storms (see Dune erosion); the longer timescale and greater closure depth are most relevant for estimating the impact of sea level rise (see the article Bruun rule).
Closure depth formulas
Hallermeier (1981, 1983)[2][3] defined three profile zones, i.e. a littoral zone which is usually called upper shoreface, a shoal or buffer zone which is usually called lower shoreface and an offshore zone or shelf zone. This partition defines two closure depths, namely:
- an “inner” (closer to shore) closure depth [math]h_{in}[/math] corresponding to the seaward limit of the upper shoreface, and
- an “outer” or “lower” (further from shore) closure depth [math]h_{out}[/math] corresponding to the seaward limit of the lower shoreface.
Hallermeier (1981)[2] derived for the inner closure depth the formula
[math]h_{in} = 2.28 H_{12h/y}- 68.5 (\Large\frac{ H_{12h/y}^2}{g T_{12h/y}^2}\normalsize), \qquad (1)[/math]
where [math]H_{12h/y}[/math] is the effective wave height just seaward of the breaker zone that is exceeded for 12 hours per year, i.e. the significant wave height with a probability of yearly exceedance of 0.137%, [math] T_{12h/y}[/math] is the wave period associated with [math] H_{12h/y}[/math], and [math]g[/math] is the acceleration of gravity.
The first term in the formula (1) is directly proportional to wave height and is the main contributor to the inner DoC. The second term provides a small correction associated with the wave steepness. Equation (1) can be further generalized to incorporate other time scales by introducing into it a significant wave height exceeded 12 hours in a particular time interval. The theoretical background of the inner DoC [math]h_{in}[/math] is based on its relation to the mobility number [math]\Phi[/math], as explained in the appendix. According to Eq. (1), [math]h_{in}[/math] is solely related to the wave parameters, irrespective of typical sediment diameters, ranging between 0.16 and 0.42 mm, as validated and described by Hallermeier (1978, 1981)[4][2].
The outer closure depth [math]h_{out}[/math] corresponds to the depth below which waves under average conditions do not interact with the seabed. It is sometimes called the "wavebase" or the maximum depth of extreme bed activity and sediment transport (Depth of Transport; DoT)[5]. For the outer closure depth Hallermeier (1983)[3] derived the formula (see appendix)
[math]h_{out} = 0.013 \,H_s T_s \, \sqrt{\Large\frac{g}{d_{50} (s-1)}\normalsize}, \qquad (2)[/math]
where [math]H_s[/math] and [math]T_s[/math] are the significant wave height and period respectively, [math]d_{50}[/math] is the median sediment diameter and [math]s[/math] is the ratio of specific gravity of sand to that of fluid (about 2.65). The outer closure depth [math]h_{out}[/math] depends on both hydrodynamic and sedimentological parameters, in contrast with [math]h_{in}[/math]. Both closure depths refer to MLW (mean low water) conditions.
Houston (1995)[6] simplified Hallermeier’s formulation using properties of a Pierson-Moskowitz wave spectrum (see Statistical description of wave parameters) and a modified exponential distribution of significant wave height over time to express the DoC in terms of mean annual significant wave height. Following Houston’s approach, the Hallermeier equation can be expressed in the form:
[math]h_{in} = 8.9 \overline {H_{s}} . \qquad (3) [/math]
In the original formulation of Hallermeier (1981)[2] and subsequent modifications, the DoC was defined based on the largest wave height exceeded 12 hours per year. This definition incorporates a time element, but the exact event associated with the value of wave height is ambiguous. Depending on changes in storm activity and wave conditions from year to year, the predicted DoC can vary substantially. In order to determine a representative value of the DoC based on this definition, wave conditions averaged over a period of several years must be employed. A useful extension of calculating the DoC based on average annual wave conditions is to relate the DoC to a particular time period of interest over which specific storm events or seasonal wave conditions occur. A similar “wave-by-wave” interpretation of the DoC was introduced by Kraus and Harikai (1983)[7]. In a wave-by-wave or event approach, the DoC can be associated with a recurrence frequency or return period for a particular storm. The return period should be associated with the wave height, not with the storm surge.
Comparison with field data
The formulas of Hallemeier refer to conditions for sand transport across the closure depth. However, sand transport measurements across depth contours representative for average or extreme conditions are hardly feasible. The closure depth in the field is therefore usually related to morphological or sedimentary features:
- a zone of minimum sand accretion or erosion (according to the definition of closure depth)
- a discontinuity of the shoreface slope or a discontinuity in the shoreface sediment composition.
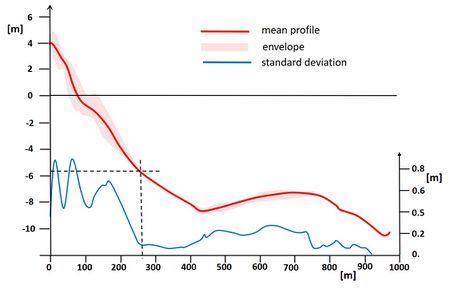
The first feature is illustrated in Fig. 1 by Krauss et al. (1998)[1], displaying [math]h_{in}[/math] and [math]h_{out}[/math] showing the result of surveys of a shoreface profile on the US Atlantic coast. The envelope of recorded elevations (above and below the mean) in any profile survey over the 4-year interval of available data and the standard deviation of depths are plotted as functions of the distance offshore. The envelope tends to converge in the depth range of 5 to 6 m for this particular profile, seaward of which the profile elevations separate over the crests of the shoals. Formation of the offshore shoals can be attributed to earlier coastal and geologic processes and not to offshore movement of sediment from the present beach. The convergence of the envelope landward of the offshore shoals indicates that movement of sediment on the shoals is not directly related to sediment exchange on the nearshore profile. For the profile data shown in Fig. 1, corresponding to a 4-year time interval, [math]h_{in}[/math] is approximately 5.5 m. The outer depth [math]h_{out}[/math] is situated around the 10 m depth contour, where no accretion or erosion is observed during the survey period. The Hallermeier formula (1) predicts an inner closure depth [math]h_{in} \approx[/math] 6 m, in reasonable agreement with the profile data. Formula (2) gives for the outer closure depth at Ocean City ([math]H_s[/math]=1 m, [math]T_s[/math] = 6 s, [math]d_{50}[/math]=0.3 mm)[8] a value of about 11 m, also in reasonable agreement.
Udo et al. (2020)[9] tested equations (1) and (2) using observed values for [math]H_{12h/y}[/math] and [math]T_{12h/y}[/math] at different field sites around Japan where observed profile data were available for at least 5 years. Inner DoC was determined by analysing the envelope of the profile data. They concluded that the coefficients in equation (1), although providing acceptable estimates, appear to be location dependent, overestimating DoC along the Pacific Ocean side and underestimating DoC along the Sea of Japan side.
Birkemeier (1985)[10] compared Eq. (1) with 16 months observations of coastal profiles on the Pacific Ocean and the Gulf of Mexico. He concluded that Eq. (1) overpredicts the closure depth derived from these data and proposed a modified version:
[math]h_{in} = 1.75 H_{12h/y}- 57.9 (\Large\frac{ H_{12h/y}^2}{g T_{12h/y}^2}\normalsize). \qquad (4)[/math]
It produces a smaller estimate of the depth of closure than the Hallermeier equation (1) for given wave conditions.
Aragones et al. (2018)[11] derived depth of closure estimates by analysing trend changes in the grain size distribution of several coastal profiles of the Mediterranean coast near Valencia. They argued that the DoC is situated at a certain depth where the tendency of seaward decreasing grain size [math]d_{50}[/math] changes into an increasing trend before decreasing further offshore again. This local grain size minimum coincided with the closure depth derived from the convergence of the profile envelope. However, the depth was substantially smaller than the closure depth predicted by Hallermeier's formula (1) and also smaller than predicted by the formula (4) of Birkemeier.
Limitation of the closure depth concept
The criterion of (almost) zero wave-induced sediment transport underlying the Hallermeier formulas (1) and (2) does not necessarily correspond to the criterion of (almost) zero depth profile change. Zero depth profile change may arise, for example, in the situation where depth change due to sediment transport across the DoC contour derived from profile data is compensated by accretion or erosion due to gradients in longshore sediment transport[12]. Another issue is that depth change of the lower shoreface which is below the detection limit can amount to a considerable sediment flux when integrated over the whole lower shoreface [5]. Insight into the local coastal dynamics is therefore required when applying the closure depth concept.
The Hallermeier formulas are based on the assumption that sediment transport on the shoreface is dominated by wave action and that the contribution of other drivers of sediment transport can be ignored. This may be a reasonable assumption for many shores, especially exposed microtidal coasts. However, it cannot be expected that the Hallermeier formulas are applicable in situations where this is not the case. Examples are: (1) macrotidal coasts, where combined wave- and tide-driven sediment transport across the DoC contour can be much larger than sediment transport driven only by waves[5]; (2) coasts where important sediment transport across the shoreface result from up- and downwelling currents induced by wind stress and density gradients[12]. In some situations the determination of wave characteristics on the lower shoreface may not be straightforward. Valiente et al. (2019)[5] observed that on the macrotidal, embayed and high-energy coastline of SW England, offshore wave conditions do not well represent wave conditions at the toe of the lower shoreface due to the presence of rocky headlands.
Hartman and Kennedy (2016)[13] argue that considering only the annual 12h extreme conditions for the inner DoC ignores the potential impact of more frequent less severe storm conditions. This can be important in tropical regions where cyclones generate extreme waves, but with such short durations that they have little opportunity to move large amounts of sediment.
Appendix
Hallermeier (1978)[4] based the closure depth formulas (1) and (2) on estimates for the mobility parameter
[math]\Phi=\Large\frac{U_b^2}{(s-1)gd_{50}}\normalsize , \qquad (A1)[/math]
where [math]\; U_b \equiv a \pi /T[/math] is the wave orbital velocity amplitude and [math]2a[/math] the wave orbital excursion. The mobility parameter is related to the Shields parameter [math]\Theta[/math], which represents the wave energy available to lift a sediment particle from the seabed. The relationship is given by [math]\Theta = ½ f_w \, \Phi[/math], where [math]f_w[/math] is the wave-induced bed friction coefficient, which can be determined from the experimental relationships [math]f_w=0.00251 \, \exp(5\, (a/d_{50})^{-0.19}) \;[/math][14] or [math]f_w=0.05 \, (a/d_{50})^{-0.25} \;[/math][15]. The formula (1) for the inner closure depth [math]h_{in}[/math] was based on the condition that only 12 hour per year wave action at this depth is strong enough to produce substantial suspended sediment transport at this depth, corresponding to flattening of bed ripples. Hallermeier found from flume experiments that this occurred for a wave orbital amplitude [math]U_b[/math] that primarily depended on depth:
[math]U_{b}^2 \approx 0.03 \, (s-1) g \, h_{in} . \qquad (A2)[/math]
The wave orbital velocity [math]U_b[/math] can be expressed as a function of the closure depth [math]h_{in}[/math] by using linear wave theory and the assumption of negligible energy loss on the lower shoreface, [math]c_g \, E = c_{0g} E_0[/math], where [math]c_g[/math] is the wave group velocity, [math]E= \frac{1}{8} g \rho H^2[/math] the wave energy at the closure depth and where offshore deep water is indicated by the subscript [math]0[/math] – see Shallow-water wave theory for explanations. Equation (A1) can then be solved numerically. The solution for the inner closure depth can be approximated by the explicit expression (1). A remarkable feature is that this expression does not depend on the grain size [math]d_{50}[/math]. In fact, Hallermeier noted that the formula for the closure depth gave the most accurate predictions for small grain sizes, which are normally found on the lower shoreface, seaward of the closure depth.
Hallermeier based his expression for the outer closure depth [math]h_{out}[/math] on the condition that no wave-induced sediment transport occurs at this depth. The critical value of the mobility parameter found from the flume experiments was
[math]\Phi \approx 8 . \qquad (A3)[/math]
The corresponding wave orbital velocity [math]U_b[/math] for grain size [math]d_{50}[/math]= 0.25 mm is about 0.18 m/s and the Shields parameter [math]\Theta \approx 4 \, f_w \approx 0.04[/math]. The outer sediment depth [math]h_{out}[/math] can be derived from Eq. (A2) using linear wave theory. The result can be approximated by Eq. (2).
Related articles
References
- ↑ 1.0 1.1 1.2 1.3 Kraus, N. C., Larson, M. and Wise, R. A. 1998. Depth of Closure in Beach-fill Design. Coastal Engineering Technical Note CETN II-40, 3/98, U.S. Army Engineer Waterways Experiment Station, Vicksburg, MS.
- ↑ 2.0 2.1 2.2 2.3 Hallermeier, R. J. 1981. A Profile Zonation for Seasonal Sand Beaches from Wave Climate. Coastal Engineering. 4: 253-277.
- ↑ 3.0 3.1 Hallermeier, R. J. 1983. Sand Transport Limits in Coastal Structure Design, Proceedings, Coastal Structures ’83, American Society of Civil Engineers, pp. 703-716.
- ↑ 4.0 4.1 Hallermeier, R. J. 1978. Uses for a calculated limit depth to beach erosion. Proceedings, 16th Coastal Engineering Conference, American Society of Civil Engineers, pp. 1493 - 1512.
- ↑ 5.0 5.1 5.2 5.3 Valiente, N.C., Masselink, G., Scott, T., Conley, D. and McCarroll, R.J. 2019. Role of waves and tides on depth of closure and potential for headland bypassing. Marine Geology 407: 60–75 Cite error: Invalid
<ref>tag; name "V19" defined multiple times with different content Cite error: Invalid<ref>tag; name "V19" defined multiple times with different content Cite error: Invalid<ref>tag; name "V19" defined multiple times with different content - ↑ Houston, J. R. 1995. Beach-fill volume required to produce specified dry beach width. Coastal Engineering Technical Note 11-32, U.S. Army Engineer Waterways Experiment Station, Vicksburg, MS.
- ↑ Kraus, N. C., and Harikai, S. 1983. Numerical model of the shoreline change at Oarai Beach CoastaI Engineering 7: 1-28.
- ↑ Stauble, D.K., Garcia, A.W., Kraus, N.C., Grosskop, W.G. and Bass, G.P. 1993. Beach Nourishment Project Response and Design Evaluation: Ocean City, Maryland Report 1 1988-1992. USACE
- ↑ Udo, K., Ranasinghe, R. and Takeda, Y. 2020. An assessment of measured and computed depth of closure around Japan. Sci. Rep. 10, 2987
- ↑ Birkemeier, W. A. 1985. Field data on seaward limit of profile change. Journal of Waterway, Port, Coastal and Ocean Engineering 111(3): 598-602.
- ↑ Aragonés, L., Ignacio Pagán, J., López, I. and Serra, J.C. 2018. Depth of closure: New calculation method based on sediment data. Int. J. Sediment Res. 33: 198–207
- ↑ 12.0 12.1 Anthony, E.J. and Aagaard, T. 2020. The lower shoreface: Morphodynamics and sediment connectivity with the upper shoreface and beach. Earth-Science Reviews 210, 103334
- ↑ Hartman, M. and Kennedy, A.B. 2016. Depth of closure over large regions using airborne bathymetric lidar. Marine Geology 379: 52–63
- ↑ Swart, D.H. 1976. Coastal sediment transport. Computation of longshore transport. rep. R968: Part I. WL Delft Hydraulics, Delft
- ↑ Fredsoe J. and Deigaard R. 1992. Mechanics of Coastal Sediment Transport. World Scientific Publ., Singapore
|
