Difference between revisions of "Wave run-up"
Dronkers J (talk | contribs) |
Dronkers J (talk | contribs) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 12: | Line 12: | ||
By waves is meant: waves generated by wind (locally or on the ocean) or waves generated by incidental disturbances of the sea surface such as tsunamis, seiches or ship waves. Wave run-up is often indicated with the symbol <math> R </math>. | By waves is meant: waves generated by wind (locally or on the ocean) or waves generated by incidental disturbances of the sea surface such as tsunamis, seiches or ship waves. Wave run-up is often indicated with the symbol <math> R </math>. | ||
| − | For waves collapsing on the beach, a first order-of-magnitude estimate is given by the empirical formula of Hunt (1959) <ref>Hunt, I.A. 1959. Design of seawalls and breakwaters. J. Waterw. Harbors Division ASCE 85: 123–152</ref><ref>Holman, R.A. and Sallenger, A.H. 1985. Setup and swash on a natural beach. J. Geophys. Res. 90: 945–953</ref><ref>Atkinson, A.L., Power, H.E., Moura, T., Hammond, T., Callaghan, D.P. and Baldock, T.E. 2017. Assessment of runup predictions by empirical models on non-truncated beaches on the south-east Australian coast. Coast. Eng. 119: 15–31</ref>, | + | For waves collapsing on the beach, a first order-of-magnitude estimate is given by the empirical formula of Hunt (1959) <ref>Hunt, I.A. 1959. Design of seawalls and breakwaters. J. Waterw. Harbors Division ASCE 85: 123–152</ref><ref>Holman, R.A. and Sallenger, A.H. 1985. Setup and swash on a natural beach. J. Geophys. Res. 90: 945–953</ref><ref name=A17>Atkinson, A.L., Power, H.E., Moura, T., Hammond, T., Callaghan, D.P. and Baldock, T.E. 2017. Assessment of runup predictions by empirical models on non-truncated beaches on the south-east Australian coast. Coast. Eng. 119: 15–31</ref>, |
<math>R \sim \eta_u + H \xi , </math> | <math>R \sim \eta_u + H \xi , </math> | ||
| Line 20: | Line 20: | ||
<math>\xi = \Large\frac{ m}{\sqrt{H/L}}\normalsize = T \, m \, \Large\sqrt{\frac{g}{2\pi H}}\normalsize , \qquad (2)</math> | <math>\xi = \Large\frac{ m}{\sqrt{H/L}}\normalsize = T \, m \, \Large\sqrt{\frac{g}{2\pi H}}\normalsize , \qquad (2)</math> | ||
| − | where <math>L = g T^2/(2 \pi)</math> is the offshore wave length, <math>m = \tan \beta</math> is the beach slope and <math>T</math> is the wave period. | + | where <math>L = g T^2/(2 \pi)</math> is the offshore wave length, <math>m = \tan \beta</math> is the beach slope and <math>T</math> is the peak wave period. |
| − | The horizontal wave incursion is approximately given by <math> R / | + | The horizontal wave incursion is approximately given by <math> R / m</math>. |
| − | Many other empirical formulas have been proposed for the run-up. A popular formula for the run-up <math> R_2</math> exceeded by only 2 % of the waves has been developed by Stockdon et al. (2006<ref name=S6>Stockdon, H.F., Holman, R.A., Howd, P.A. and Sallenger, A.H. 2006. Empirical parameterization of setup, swash, and runup. Coast. Eng. 53: 573–588</ref>), based on a large dataset: | + | Many other empirical formulas have been proposed for the run-up. A popular formula for the run-up <math> R_2</math> exceeded by only 2 % of the waves for given <math>H, L</math> has been developed by Stockdon et al. (2006<ref name=S6>Stockdon, H.F., Holman, R.A., Howd, P.A. and Sallenger, A.H. 2006. Empirical parameterization of setup, swash, and runup. Coast. Eng. 53: 573–588</ref>), based on a large dataset: |
<math> R_2 = 1.1 \; (\eta_u + 0.5 \sqrt{S_w^2 + S_{ig}^2} \, ) , \qquad \xi \ge 0.3 , \qquad R_2= 0.043 \; \sqrt{HL} , \qquad \xi < 0.3 , \qquad (3) </math> | <math> R_2 = 1.1 \; (\eta_u + 0.5 \sqrt{S_w^2 + S_{ig}^2} \, ) , \qquad \xi \ge 0.3 , \qquad R_2= 0.043 \; \sqrt{HL} , \qquad \xi < 0.3 , \qquad (3) </math> | ||
| Line 29: | Line 29: | ||
where <math>\eta_u = 0.35 H \xi</math> is the wave set-up, <math>S_w=0.75 H \xi</math> is the swash uprush related to incident waves and <math>S_{ig}=0.06 \sqrt{HL}</math> is the additional uprush related to [[infragravity waves]]. The factor 1.1 takes into account the non-Gaussian distribution of run-up events. | where <math>\eta_u = 0.35 H \xi</math> is the wave set-up, <math>S_w=0.75 H \xi</math> is the swash uprush related to incident waves and <math>S_{ig}=0.06 \sqrt{HL}</math> is the additional uprush related to [[infragravity waves]]. The factor 1.1 takes into account the non-Gaussian distribution of run-up events. | ||
| − | From an inventory of run-up formulas by Gomes da Silva et al. (2020<ref>Gomes da Silva, P., Coco, G., Garnier, R. and Klein, A.H.F. 2020. On the prediction of runup, setup and swash on beaches. Earth-Science Reviews 204, 103148</ref>), it appears that for steep beaches (<math> m > 0.1</math>) the run-up increases with increasing beach slope (approximately linear dependance<ref name=NH>Nielsen, P. and Hanslow, D.J. 1991. Wave runup distributions on natural beaches. J. Coast. Res. 7: 1139–1152</ref>), while for gently sloping dissipative beaches (<math> m < 0.1</math>) the dependence on beach slope is weak or absent<ref name=NH/><ref name=S6/>. In these latter cases, run-up is dominated by [[infragravity waves]], that yield a small run-up that increases with increasing wave height (approximately linear dependence<ref>Ruessink, B.G., Kleinhans, M.G. and Van Den Beukel, P.G.L. 1998. Observations of swash under highly dissipative conditions. J. Geophys. Res. 103: 3111–3118</ref><ref>Ruggiero, P., Holman, R. A. and Beach, R. A. 2004. Wave run-up on a high-energy dissipative beach. J. Geophys. Res. 109, C06025, doi:10.1029/2003JC002160</ref>). Field observations<ref>Matsuba, Y. and Shimozono, T. 2021. Analysis of the contributing factors to infragravity swash based on long-term observations. Coastal Engineering 169, 103957</ref> and numerical models<ref>Guza, R.T. and Feddersen, F. 2012. Effect of wave frequency and directional spread on shoreline runup. Geophys. Res. Lett. 39: 1–5</ref> also point to a dependence of infragravity [[swash]] on the frequency spread and the directional spread of incident waves. The largest infragravity swash | + | From an inventory of run-up formulas by Gomes da Silva et al. (2020<ref>Gomes da Silva, P., Coco, G., Garnier, R. and Klein, A.H.F. 2020. On the prediction of runup, setup and swash on beaches. Earth-Science Reviews 204, 103148</ref>), it appears that for steep beaches (<math> m > 0.1</math>) the run-up increases with increasing beach slope (approximately linear dependance<ref name=NH>Nielsen, P. and Hanslow, D.J. 1991. Wave runup distributions on natural beaches. J. Coast. Res. 7: 1139–1152</ref>), while for gently sloping dissipative beaches (<math> m < 0.1</math>) the dependence on beach slope is weak or absent<ref name=NH/><ref name=S6/>. In these latter cases, run-up is dominated by [[infragravity waves]], that yield a small run-up that increases with increasing wave height (approximately linear dependence<ref>Ruessink, B.G., Kleinhans, M.G. and Van Den Beukel, P.G.L. 1998. Observations of swash under highly dissipative conditions. J. Geophys. Res. 103: 3111–3118</ref><ref>Ruggiero, P., Holman, R. A. and Beach, R. A. 2004. Wave run-up on a high-energy dissipative beach. J. Geophys. Res. 109, C06025, doi:10.1029/2003JC002160</ref>). Field observations<ref>Matsuba, Y. and Shimozono, T. 2021. Analysis of the contributing factors to infragravity swash based on long-term observations. Coastal Engineering 169, 103957</ref> and numerical models<ref>Guza, R.T. and Feddersen, F. 2012. Effect of wave frequency and directional spread on shoreline runup. Geophys. Res. Lett. 39: 1–5</ref> also point to a dependence of infragravity [[swash]] on the frequency spread and the directional spread of incident waves. The largest infragravity swash has been observed for incident waves with a small directional spread and a large frequency spread. |
In cases where the backshore berm or foredune of dissipative sandy beaches is artificially protected with gravel or cobbles, the run-up <math> R_2</math> exceeded by only 2 % of the waves when the water level during storms reaches higher than the toe of the cobble berm revetment, can be estimated from the approximate empirical formula<ref>Blenkinsopp, C.E., Bayle, P.M., Martins, K., Foss, O.W., Almeida, L.-P., Kaminsky, G.M., Schimmels, S. and Matsumoto, H. 2022. Wave runup on composite beaches and dynamic cobble berm revetments. Coastal Engineering 176, 104148</ref> | In cases where the backshore berm or foredune of dissipative sandy beaches is artificially protected with gravel or cobbles, the run-up <math> R_2</math> exceeded by only 2 % of the waves when the water level during storms reaches higher than the toe of the cobble berm revetment, can be estimated from the approximate empirical formula<ref>Blenkinsopp, C.E., Bayle, P.M., Martins, K., Foss, O.W., Almeida, L.-P., Kaminsky, G.M., Schimmels, S. and Matsumoto, H. 2022. Wave runup on composite beaches and dynamic cobble berm revetments. Coastal Engineering 176, 104148</ref> | ||
| Line 37: | Line 37: | ||
where <math>h_{toe}</math> is the water depth at the toe of the berm and <math>m_{berm}</math> is the berm slope. | where <math>h_{toe}</math> is the water depth at the toe of the berm and <math>m_{berm}</math> is the berm slope. | ||
| − | The general applicability of empirical formulas for run-up prediction based on simple parametric representations of beach and shoreface is limited due to the influence of the more detailed characteristics of the local shoreface bathymetry (e.g., curvature of the beach profile or swash acceleration along the horn of a [[Beach cusps|beach cusp]] embayment<ref>Kim, L.N., Brodie, K.L., Cohn, N.T., Giddings, S.N. and Merrifield, M. 2023. Observations of beach change and runup, and the performance of empirical runup parameterizations during large storm events. Coastal Engineering 184, 104357</ref>). | + | The accuracy (root-mean-square deviation) of run-up predictions using empirical formulas such as (1), (3) or (4) is usually not better than <math>0.25 \, R</math>.<ref name=A17/> The general applicability of empirical formulas for run-up prediction based on simple parametric representations of beach and shoreface is limited due to the influence of the more detailed characteristics of the local beach and shoreface bathymetry (e.g., beach permeability and groundwater level, curvature of the beach profile, crescentic bars, or swash acceleration along the horn of a [[Beach cusps|beach cusp]] embayment<ref>Kim, L.N., Brodie, K.L., Cohn, N.T., Giddings, S.N. and Merrifield, M. 2023. Observations of beach change and runup, and the performance of empirical runup parameterizations during large storm events. Coastal Engineering 184, 104357</ref>). The tide level may influence the wave run-up due to wave breaking on [[nearshore sandbars]].<ref>Guedes, R.M.C., Bryan, K.R., Coco, G. and Holman, R.A. 2011. The effects of tides on swash statistics on an intermediate beach. J. Geophys. Res. 116, C04008</ref> The applicability of empirical formulas for the [[wave set-up]], which is a substantial component of the run-up, is limited for similar reasons. Accurate estimates of the wave run-up require in-situ observations or detailed numerical models. |
| Line 49: | Line 49: | ||
==References== | ==References== | ||
<references/> | <references/> | ||
| + | |||
| + | |||
| + | {{author | ||
| + | |AuthorID=120 | ||
| + | |AuthorFullName=Job Dronkers | ||
| + | |AuthorName=Dronkers J}} | ||
[[Category:Beaches]] | [[Category:Beaches]] | ||
Latest revision as of 09:14, 1 September 2024
Definition of Wave run-up:
Wave run-up is the maximum onshore elevation reached by waves, relative to the shoreline position in the absence of waves.
This is the common definition for Wave run-up, other definitions can be discussed in the article
|
Notes
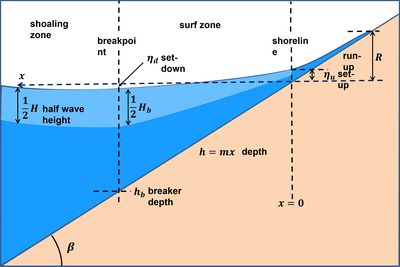
Wave run-up is the sum of wave set-up and swash uprush (see Swash zone dynamics) and must be added to the water level reached as a result of tides and wind set-up (Fig. 1). Wave run-up on a beach is generally due to so-called swash bores: the uprush of waves after final collapse on the beach. Wave run-up is an important parameter for assessing the safety of sea dikes or coastal settlements.
By waves is meant: waves generated by wind (locally or on the ocean) or waves generated by incidental disturbances of the sea surface such as tsunamis, seiches or ship waves. Wave run-up is often indicated with the symbol [math] R [/math].
For waves collapsing on the beach, a first order-of-magnitude estimate is given by the empirical formula of Hunt (1959) [1][2][3],
[math]R \sim \eta_u + H \xi , [/math]
where [math]\eta_u \sim 0.2 H[/math] is the wave set-up, [math]H[/math] is the offshore significant wave height and [math]\xi[/math] is the surf similarity parameter,
[math]\xi = \Large\frac{ m}{\sqrt{H/L}}\normalsize = T \, m \, \Large\sqrt{\frac{g}{2\pi H}}\normalsize , \qquad (2)[/math]
where [math]L = g T^2/(2 \pi)[/math] is the offshore wave length, [math]m = \tan \beta[/math] is the beach slope and [math]T[/math] is the peak wave period. The horizontal wave incursion is approximately given by [math] R / m[/math].
Many other empirical formulas have been proposed for the run-up. A popular formula for the run-up [math] R_2[/math] exceeded by only 2 % of the waves for given [math]H, L[/math] has been developed by Stockdon et al. (2006[4]), based on a large dataset:
[math] R_2 = 1.1 \; (\eta_u + 0.5 \sqrt{S_w^2 + S_{ig}^2} \, ) , \qquad \xi \ge 0.3 , \qquad R_2= 0.043 \; \sqrt{HL} , \qquad \xi \lt 0.3 , \qquad (3) [/math]
where [math]\eta_u = 0.35 H \xi[/math] is the wave set-up, [math]S_w=0.75 H \xi[/math] is the swash uprush related to incident waves and [math]S_{ig}=0.06 \sqrt{HL}[/math] is the additional uprush related to infragravity waves. The factor 1.1 takes into account the non-Gaussian distribution of run-up events.
From an inventory of run-up formulas by Gomes da Silva et al. (2020[5]), it appears that for steep beaches ([math] m \gt 0.1[/math]) the run-up increases with increasing beach slope (approximately linear dependance[6]), while for gently sloping dissipative beaches ([math] m \lt 0.1[/math]) the dependence on beach slope is weak or absent[6][4]. In these latter cases, run-up is dominated by infragravity waves, that yield a small run-up that increases with increasing wave height (approximately linear dependence[7][8]). Field observations[9] and numerical models[10] also point to a dependence of infragravity swash on the frequency spread and the directional spread of incident waves. The largest infragravity swash has been observed for incident waves with a small directional spread and a large frequency spread.
In cases where the backshore berm or foredune of dissipative sandy beaches is artificially protected with gravel or cobbles, the run-up [math] R_2[/math] exceeded by only 2 % of the waves when the water level during storms reaches higher than the toe of the cobble berm revetment, can be estimated from the approximate empirical formula[11]
[math] R_2 \approx 4.14 \, h_{toe} m_{berm} +0.66 , \qquad (4) [/math]
where [math]h_{toe}[/math] is the water depth at the toe of the berm and [math]m_{berm}[/math] is the berm slope.
The accuracy (root-mean-square deviation) of run-up predictions using empirical formulas such as (1), (3) or (4) is usually not better than [math]0.25 \, R[/math].[3] The general applicability of empirical formulas for run-up prediction based on simple parametric representations of beach and shoreface is limited due to the influence of the more detailed characteristics of the local beach and shoreface bathymetry (e.g., beach permeability and groundwater level, curvature of the beach profile, crescentic bars, or swash acceleration along the horn of a beach cusp embayment[12]). The tide level may influence the wave run-up due to wave breaking on nearshore sandbars.[13] The applicability of empirical formulas for the wave set-up, which is a substantial component of the run-up, is limited for similar reasons. Accurate estimates of the wave run-up require in-situ observations or detailed numerical models.
Related articles
References
- ↑ Hunt, I.A. 1959. Design of seawalls and breakwaters. J. Waterw. Harbors Division ASCE 85: 123–152
- ↑ Holman, R.A. and Sallenger, A.H. 1985. Setup and swash on a natural beach. J. Geophys. Res. 90: 945–953
- ↑ 3.0 3.1 Atkinson, A.L., Power, H.E., Moura, T., Hammond, T., Callaghan, D.P. and Baldock, T.E. 2017. Assessment of runup predictions by empirical models on non-truncated beaches on the south-east Australian coast. Coast. Eng. 119: 15–31
- ↑ 4.0 4.1 Stockdon, H.F., Holman, R.A., Howd, P.A. and Sallenger, A.H. 2006. Empirical parameterization of setup, swash, and runup. Coast. Eng. 53: 573–588
- ↑ Gomes da Silva, P., Coco, G., Garnier, R. and Klein, A.H.F. 2020. On the prediction of runup, setup and swash on beaches. Earth-Science Reviews 204, 103148
- ↑ 6.0 6.1 Nielsen, P. and Hanslow, D.J. 1991. Wave runup distributions on natural beaches. J. Coast. Res. 7: 1139–1152
- ↑ Ruessink, B.G., Kleinhans, M.G. and Van Den Beukel, P.G.L. 1998. Observations of swash under highly dissipative conditions. J. Geophys. Res. 103: 3111–3118
- ↑ Ruggiero, P., Holman, R. A. and Beach, R. A. 2004. Wave run-up on a high-energy dissipative beach. J. Geophys. Res. 109, C06025, doi:10.1029/2003JC002160
- ↑ Matsuba, Y. and Shimozono, T. 2021. Analysis of the contributing factors to infragravity swash based on long-term observations. Coastal Engineering 169, 103957
- ↑ Guza, R.T. and Feddersen, F. 2012. Effect of wave frequency and directional spread on shoreline runup. Geophys. Res. Lett. 39: 1–5
- ↑ Blenkinsopp, C.E., Bayle, P.M., Martins, K., Foss, O.W., Almeida, L.-P., Kaminsky, G.M., Schimmels, S. and Matsumoto, H. 2022. Wave runup on composite beaches and dynamic cobble berm revetments. Coastal Engineering 176, 104148
- ↑ Kim, L.N., Brodie, K.L., Cohn, N.T., Giddings, S.N. and Merrifield, M. 2023. Observations of beach change and runup, and the performance of empirical runup parameterizations during large storm events. Coastal Engineering 184, 104357
- ↑ Guedes, R.M.C., Bryan, K.R., Coco, G. and Holman, R.A. 2011. The effects of tides on swash statistics on an intermediate beach. J. Geophys. Res. 116, C04008
Please note that others may also have edited the contents of this article.
|