Dam break flow

From Coastal Wiki
Revision as of 21:39, 1 May 2020 by Dronkers J (talk | contribs)
Jump to: navigation, search

Dam break flow

This article discusses the often catastrophic flows that result from the sudden collapse of high dams that protect low-lying land. The mechanisms causing dam breaks are not dealt with; for this the reader is referred to the extensive literature existing on this subject, see for example Zhang et al. (2016) [1] and Almog et al. (2011) [2].


Introduction

Fig. 1. Sea dikes protecting low-lying polders in the Netherlands were breached during the extreme storm surge of 31 January 1953.


Dam failure can lead to disastrous situations. Most dam-break tragedies are related to the collapse of reservoir dams in mountain rivers. The failure of sea dikes can also cause major disasters, although the level difference in this case is not as large. A dramatic example is the failure of more than hundred sea dikes in the Netherlands during the extreme storm surge of 1953, see Fig. 1. Many of these dikes protected polders lying a few meters below the average sea level, while the storm surge level in the tidal inlets reached up to five meters. Rapid flooding killed almost two thousand people who were unable to flee in time to safe places [3]. The most common dam failure mechanisms are related to overtopping and seepage (also called piping or internal erosion)[4]. In the case of the 1953 storm surge, overtopping and subsequent scour of the interior dike slope was the most important dike failure mechanism.




Fig. 2. Left panel: Schematic representation of water retention behind a dam. Right panel: Positive downstream and negative upstream surges following instantaneous dam removal.


The consequences of dam failure have been studied for more than a century. It nevertheless remains a challenging topic due to the high non-linearity of the flood wave propagation. The problem can be tackled with numerical models, but rough estimates and insight into the tidal wave dynamics can be obtained with analytical solution methods.


Frictionless dam-break flow: analytical solution

Analytical solutions relate to idealized situations as depicted in Fig. 2. The initial situation consists of an infinite reservoir with a water level that is [math] h_0 [/math] higher than the horizontal ground level downstream of the dam. Dam break is simulated by instantaneous removal of the dam. This causes a positive surge in the positive [math] x [/math]-direction and a negative surge in the negative [math] x [/math]-direction. The floor is dry in front of the positive surge (water level [math]h = 0[/math]) and the water body behind the negative surge is undisturbed (water level [math]h = h_0 [/math] and current speed [math] u = 0 [/math]).

Fig. 3. The earth-filled South Fork Dam on Lake Conemaugh (Pennsylvania, US) collapsed in 1889, killing 2,209 people in downstream villages.



The study of dam break-flow was triggered by several dam failures in the 19th century, in particular the breach of the South Fork Dam in Pennsylvania (USA) in 1889, Fig. 3. Three years later Ritter [5] published an exact analytical solution for dam-break flow by assuming that frictional effects can be ignored. The derivation is given in box 1. According to this solution, the tip of the positive surge advances at high speed (supercritical flow) given by [math] u_f = 2 c_0[/math], where [math]c_0 = \sqrt {gh_0}[/math] and [math] g [/math] is the gravitational acceleration. The shape of the positive and negative surge is a concave-up parabola,


[math] h(x,t) = \begin{cases} h_0 , \qquad x \lt -c_0 t \\ \Large\frac{h_0}{9}\normalsize \; (2 - \Large\frac{x}{c_0 t}\normalsize)^2 , \quad -c_0 t\lt x\lt 2c_0 t \qquad (1) \\ 0 , \qquad x \gt 2 c_0 t \end{cases} [/math]

[math]u(x,t) = \Large\frac{2 c_0}{3}\normalsize \, (1 + \Large\frac{x}{c_0 t}\normalsize) , \quad -c_0 t \lt x \lt 2 c_0 t \; . \qquad (2)[/math]


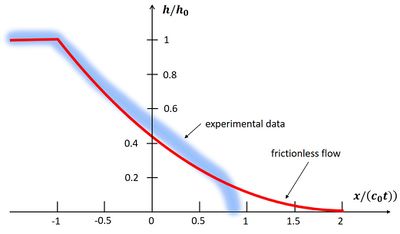
This solution is shown in Fig. 4. According to Eqs. (1, 2), the discharge through the breach per unit width is given by

[math]q = \frac{8}{27} h_0 \sqrt{g h_0}. \qquad (3) [/math]


Figure 4 also shows the shape of the dam break wave that was observed in laboratory experiments. For small values of [math] x /(c_0 t) [/math], the frictionless solution corresponds fairly well with the observations. However, the front zone is different: the shape is a bull nose, rather than a sharp edge. The front also advances more slowly; the speed of the front decreases with time and is closer to [math] u_f = c_0 [/math] than to [math] u_f = 2 c_0 [/math]. The reason for this difference is the neglect of frictional effects that are important in the thin fluid layer near the front.


Box 1. Derivation of the solution for frictionless dam break flow.


Dam-break flow with friction

Fig. 4. Wave profile after dam break. The red curve corresponds to the frictionless solution Eq. 1. The blue band represents data from different laboratory experiments performed at times [math]\small t \sim (40-80) \, \sqrt {h_0 / g}\normalsize [/math] after removal of the dam [6] [7][8]. The frictionless solution only depends on [math]x/(c_0 t)[/math]. Observed wave profiles also depend on time [math]t[/math] because of the decreasing wave tip speed.


When friction terms are included in the flow equations, there is no exact analytical solution. It is generally assumed that the frictionless flow equations are approximately valid in a short period after dam break and for small values of [math]x / (c_0 t) [/math]. In the front zone, where the water depth is small, the momentum balance is dominated by frictional momentum dissipation. If the inertia terms [math]\partial u / \partial t + u \partial u / \partial x [/math] in the momentum equation are ignored, then the current in the front region is mainly determined by the balance of gravitational acceleration [math] g \partial h / \partial x [/math] and shear stress [math]\tau[/math], the latter term being proportional to the square of the flow velocity[9][10][11][12]. With such models the shape of the bore in the friction-dominated zone is given by

[math]h(s) \propto s^{1/2} \; , [/math]

where [math]s[/math] is the distance measured from the wave front. This shape does not represent correctly the tip of the bore near [math]s=0[/math], because the boundary layer structure is more complex than suggested by the quadratic friction law[13][14][15]. The highly turbulent bore front has strong erosional power, as evidenced by field observations of very high suspended sediment concentrations associated with propagating surges[16] (see also the article Tidal bore dynamics).

The wave front speed [math]u_f[/math] decreases with time. At small times [math]t\lt \lt t_{\infty}[/math], the wave front speed varies approximately as [10]

[math]u_f \approx c_0 \, (2 – 3.45 \sqrt{t / t_{\infty}}) \; , \qquad (4) [/math]

where [math] t_{\infty} = \sqrt{(h_0/g)}/ c_D [/math] and [math]c_D[/math] is the friction coefficient (value in the range [math]\approx (1-5)\, 10^{-3}[/math]).

At large times ([math]t[/math] of the order of [math]t_{\infty}[/math]), the wave front speed varies approximately as [10]

[math]u_f \approx c_0 \sqrt{0.5 \, t_{\infty} / t} \; . \qquad (5)[/math]


Data from numerous reservoir dam breaks in the past have provided empirical formulas for the maximum discharge [math]Q_{max}[/math] through the breach [17][10]. From this data it was deduced that the width of the breach is often a function of the water volume [math]V[/math] in the reservoir (volume above breach level). A rough estimate of the width is given by [4] [math] B \approx 0.3 V ^ {1/3} [/math]. Empirical formulas for the maximum dam break discharge then yield [18] [10]

[math]Q_{max} \approx 0.04 \sqrt{g} \, V^{0.37} h_0^{1.4} \approx 0.15 h_0 \, B \, \sqrt{g h_0} \, V^{0.04} h_0^{-0.1} . \qquad (6)[/math]

From this follows an empirical estimate for the order of magnitude of the maximum discharge per unit width,

[math] q_{max} \approx 0.22 h_0 \, \sqrt{g h_0} , \qquad (7)[/math]

where we have considered a large reservoir volume ([math]V \approx 10^7 m^3[/math]) and a water depth [math]h_0 \approx 15 m[/math]. The empirical estimate (7) is about 75% of the estimate (3) given by the frictionless flow solution.


Numerical models

The analytical methods for describing dam-break flow provide a qualitative picture and some first-order estimates for the bore profile and surge speed. They can only be used in situations that can be represented schematically by a simple prismatic channel. For actual field situations, the dam-break flow must be modeled numerically. A correct simulation of the backward surge requires models of the Boussinesq type that take into account vertical fluid accelerations[19]. Practical situations are generally characterized by the complex geometry of a highly irregular river bed that evolves during the dam-break event. Current numerical models cannot easily meet the requirements for performing accurate simulations of such real events.


Related articles

Tidal bore dynamics
Tsunami


References

  1. ↑ Zhang, L., Peng, M., Chang, D. and Xu, Y. 2016. Dam failure and Risk Assessment. John Wiley and Sons, Singapore
  2. ↑ Almog, E., Kelham, P and King, R. 2011. Modes of dam failure and monitoring and measuring techniques. Environmental Agency,UK https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/290819/scho0811buaw-e-e.pdf
  3. ↑ Gerritsen, H. 2005. What happened in 1953? The Big Flood in the Netherlands in retrospect. Phil. Trans. R. Soc. A 363: 1271–1291
  4. ↑ 4.0 4.1 Froehlich, D.C. 2008. Embankment Dam Breach Parameters and Their Uncertainties. Journal of Hydraulic Engineering, ASCE 134: 1708-1721
  5. ↑ Ritter, A. 1892. Die Fortpflanzung der Wasserwellen. Zeitschrift des Vereines Deutscher Ingenieure 36: 947-954
  6. ↑ Dressler, R. 1954. Comparison of theories and experiments for the hydraulic dam-break wave. Proc. Int. Assoc. Scientific Hydrology Assemblée Générale, Rome, Italy 3 (38)M 319–328
  7. ↑ Schoklitsch, A. 1917. Über Dambruchwellen. Kaiserliche Akademie der Wissenschaften, Wien, Mathematisch-Naturwissenschaftliche Klasse, Sitzungberichte IIa, 126: 1489–1514
  8. ↑ Cavaillé,Y. 1965. Contribution à l’étude de l’écoulement variable accompagnant la vidange brusque d’une retenue. Publ. Scient. et Techn. du Ministère de l’Air, 410, Paris, France, 165
  9. ↑ Dressler, R.F. 1952. Hydraulic resistance effect upon the dambreak functions. J. Res. Natl. Bureau of Standards, 49(3): 217–225
  10. ↑ 10.0 10.1 10.2 10.3 10.4 Whitham, G.B. 1955. The effects of hydraulic resistance in the dam-break problem. Proc. Roy. Soc. of London, Serie A, 227: 399–407 Cite error: Invalid <ref> tag; name "W" defined multiple times with different content
  11. ↑ Hogg, A.J. and Pritchard, D. 2004. The effects of hydraulic resistance on dam-break and other shallow inertial flows. J. Fluid Mech. 501: 179–212
  12. ↑ Chanson, H. 2009. Application of the method of characteristics to the dam break wave problem. Journal of Hydraulic Research 47: 41–49
  13. ↑ Nielsen, P. 2018. Bed shear stress, surface shape and velocity field near the tips of dam-breaks, tsunami and wave runup velocity. Coastal Eng. 138: 126–131
  14. ↑ Baldock, T.E. 2018. Bed shear stress, surface shape and velocity field near the tips of dam-breaks, tsunami and wave runup. Discussion. Coastal Eng. 142: 77–81
  15. ↑ Nielsen, P. 2019 Bed shear stress, surface shape and velocity field near the tips of dam-breaks, tsunami and wave runup: Reply by Peter Nielsen. Coastal Engineering 152, 103513
  16. ↑ Khezri, N. and Chanson, H. 2012. Inception of bed load motion beneath a bore. Geomorphology 153: 39–47
  17. ↑ Froehlich, D.C. 2016. Predicting Peak Discharge from Gradually Breached Embankment Dam. Journal of Hydraulic Engineering, ASCE 04016041
  18. ↑ Webby, M. G. 1996. Discussion of ‘Peak outflow from breached embankment dam.’ by D. C. Froehlich. J. Water Resour. Plann. Management 122:4(316), 316–317
  19. ↑ Castro-Orgaz, O. and Chanson, H. 2017. Ritter’s dry-bed dam-break flows: positive and negative wave dynamics. Environ Fluid Mech (2017) 17:665–694


The main author of this article is Job Dronkers
Please note that others may also have edited the contents of this article.
Citation: Job Dronkers (2020): Dam break flow. Available from http://www.coastalwiki.org/wiki/Dam_break_flow [accessed on 24-11-2024]
Retrieved from "https://www.coastalwiki.org/w/index.php?title=Dam_break_flow&oldid=76636"