Seawater density

Introduction

Density gradients play a prominent role in marine hydrodynamics. The large-scale long-term mean currents in the ocean and in estuaries largely depend on the density differences between water masses. The same holds for the small-scale turbulent velocity fluctuations that are responsible for mixing processes in oceans, shelf seas and estuaries. Knowledge of the seawater density is therefore prerequisite for understanding and modelling marine processes.

The seawater density [math]\rho[/math] in the ocean mainly depends on salinity [math]S[/math], temperature [math]T[/math] and pressure [math]p[/math]. Pressure only plays a role at depths much greater than those of coastal waters. Because of the primary focus of the Coastal Wiki on coastal waters, the dependency on pressure will be ignored in this article.

Salinity-temperature dependence of seawater density

Fig. 1. Density-salinity-temperature plot. Source: NASA.

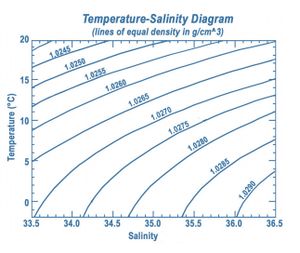
An accurate empirical expression for the density-salinity-temperature relationship for coastal waters has been derived by Fonofoff and Millard (1983). This expression holds for the temperature range [math] 0\lt T\lt 40 \;[/math] ^oC, the salinity range [math] 0 \le S\lt 42 [/math] and for pressures lower than [math]p\lt 10[/math] bar. [math]S[/math] is the practical salinity.

[math]\rho = \rho_0 + (0.8245-4.1\, 10^{-3} \,T+7.64\, 10^{-5} \,T^2-8.25\, 10^{-7} \,T^3+5.4\, 10^{-9} \,T^4)\times S \\ +(-5.7\, 10^{-3} \,+10^{-4} \,T-1.65\, 10^{-6} \,T^2)\times S^{3/2} + 4.8\, 10^{-4}\,S^2 , \qquad (1)[/math]

[math]\rho_0 =999.84+6.8 \, 10^{-2} \, T - 9.1\, 10^{-3} \, T^2+10^{-4} \, T^3-1.1 \, 10^{-6} \, T^4+6.5\, 10^{-9} \, T^5 . \qquad (2)[/math]

The density-salinity-temperature relationship is plotted in Fig. 1. More precise relationships have been established since; these relationships also include pressure effects. However, for coastal waters the increased accuracy is usually not required.

A simpler approximation of equations (1,2) with accuracy better than 1 ‰ is

[math]\rho = 999.1+ 0.77 \, (S-\Large\frac{T-15}{5.13}-\frac{(T-15)^2}{128}\normalsize) . \qquad (3)[/math]

In turbid coastal waters, the suspended sediment concentration in g / kg has to be added in this expression.

Processes induced by density differences

Seawater density decreases with increasing temperature and increases with increasing salinity. According to Eq. (3), an increase of 1 g / kg in salinity has about the same effect on the seawater density as a decrease of 4-5 ^oC in temperature. Warmer water tends to stay near the surface and saltier water near the bottom. However, warm salty water can sink to the bottom whereas cold but less salty water can rise to the surface. The balance between small changes in salinity and temperature has great importance for the ocean circulation.

Fig. 2. Schematic picture of estuarine circulation in a vertical-longitudinal section of the estuary. Red=seawater, blue=fresh water.

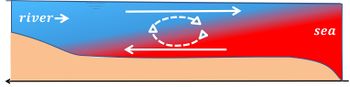
In estuaries, the density effect of salinity gradients is generally much greater than the density effect of the temperature gradients, producing vertical salinity stratification and the well-known estuarine circulation, which is driven by the density gradient along the estuarine axis, see Fig. 2. In contrast, in oceans, the density effect of temperature generally dominates the effect of salinity. In many parts of the oceans, both temperature and salinity decrease with depth.

Stratification

Fig. 3. Well-mixed (left) and stratified (right) water column. Blue=lower density, red=higher density.

A body of water is referred to as 'stable' when the density decreases from bottom to surface. This is the usual situation, also in cases where strong mixing occurs over the water column. Mixing is mainly caused by turbulence, which is generated by frictional shear stresses at the bottom and the water surface. When the production of turbulent energy in an estuary decreases, inflowing river water and seawater will be less mixed: vertical density differences force the water column into a more stratified state, with the vertical density difference concentrated around a transition layer, the so-called pycnocline, see Fig. 3. This is a nonlinear process as a result of the hydrostatic pressure differences (buoyancy principle of Archimedes) that dampen turbulent fluid fluctuations around the pycnocline; the turbulent energy production needed for mixing increases as the stratification increases.

The suppression of mixing in stratified water bodies between the surface layer and the water layer below the pycnocline can have serious consequences for the aeration of the lower layer, because this is where the most mineralization takes place and thus the oxygen demand is greatest. Especially when the water is eutrophic (high organic content) and turbid, the oxygen demand in the lower layer leads to hypoxia, resulting in severe mortality of benthic organisms in particular (see also the article Estuarine turbidity maximum).

Water and salt cannot spontaneously unmix from an existing solution (this would be contrary to the second law of thermodynamics), but a suspension of fine sediment can unmix by settling. Settling of fine sediment in turbid coastal waters can increase the density in the lower part of the water column such that a pycnocline starts to develop. Damping of turbulence around the pycnocline furthers the settling process, which can eventually lead to the formation of a fluid mud layer (see the article Dynamics of mud transport).

Overturning

Fig. 4. Schematic picture of salt fingers. Blue=lower density, red=higher density.

When denser (salty, cold) water is advected over less dense water by wind-driven or tide-driven currents, the water column becomes unstable. The denser surface water will sink trough the underlying less dense water layer. This process is called convective overturning and contributes to the mixing of water masses of different density. It can occur, for example, when seawater enters a partially mixed estuary and a strong near-surface flood current carries dense saline water over the underlying, less saline estuarine water (see also Estuarine circulation).

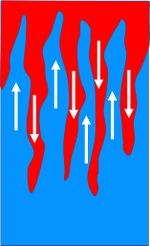
Overturning processes can also occur when surface water is heated by the sun and salinity is increased by evaporation. The density of the warm salty surface water may then exceed the density of the underlying layer of cooler water, in which case the warm salty surface water will sink through this cooler layer. The downward motion is accelerated, because the salty surface water is cooled while sinking. This leads to the formation of so-called 'salt fingers', see Fig. 4. This overturning motion is not only important for the large scale ocean circulation, but it also causes upwelling of nutrient-rich water from the bottom layer and thus stimulates primary production on which the ocean food web depends.

Related articles

Salinity

Ocean circulation

Thermohaline circulation of the oceans

Estuarine circulation

Salt wedge estuaries

References

The main author of this article is Job Dronkers Please note that others may also have edited the contents of this article. Citation: Job Dronkers (2020): Seawater density. Available from http://www.coastalwiki.org/wiki/Seawater_density [accessed on 24-11-2024] For other articles by this author see Category:Articles by Job Dronkers For an overview of contributions by this author see Special:Contributions/Dronkers J