Difference between revisions of "Long-period lunar tides"

From Coastal Wiki
Jump to: navigation, search
 
Line 80: Line 80:
 
==Appendix==
 
==Appendix==
 
The equilibrium theory of tides, taking into account the solid Earth elastic response, self-attraction and mass conservation, gives the following estimate for amplitude of the 18.6-year nodal tide<ref name=W12/>:  
 
The equilibrium theory of tides, taking into account the solid Earth elastic response, self-attraction and mass conservation, gives the following estimate for amplitude of the 18.6-year nodal tide<ref name=W12/>:  
−
<math>\quad a \approx |  7 \; (3 \, \sin^2 \theta - 1)|, \quad</math>
+
<math>\quad a \approx 7 \; | 3 \, \sin^2 \theta - 1|, \quad</math>
 
where <math>a</math> is the amplitude in mm and <math>\theta</math> the latitude in radians. The amplitude is maximum at the poles and zero at 35 degrees N/S. High (> 35<sup>o</sup>) and low (< 35<sup>o</sup>) latitudes are out-of-phase; the phase at the equator corresponds to the phase of the nodal modulation of the semidiurnal tide.  
 
where <math>a</math> is the amplitude in mm and <math>\theta</math> the latitude in radians. The amplitude is maximum at the poles and zero at 35 degrees N/S. High (> 35<sup>o</sup>) and low (< 35<sup>o</sup>) latitudes are out-of-phase; the phase at the equator corresponds to the phase of the nodal modulation of the semidiurnal tide.  
−
 
  
  

Latest revision as of 22:17, 2 July 2023

Tidal motion is the oscillation of ocean waters under the influence of the attractive gravitational forces of the moon and the sun. The frequencies of these oscillations are determined by the cycles in the motions of moon, sun and earth. The amplitude of the tidal oscillations is very small compared to ocean depths. The ocean tidal oscillation in each point can therefore be represented by a linear superposition of sinusoidal tidal components with periods derived from the various astronomical cycles.

The Earth's and Moon's orbital motion are characterized by a limited number of fundamental periods:

  • [math]1/f_1=[/math] period of lunar declination = 27.321582 days
  • [math]1/f_2 =[/math] period of solar declination = 365.242199 days
  • [math]1/f_3=[/math] period of lunar perigee rotation = 8.847 years
  • [math]1/f_4 =[/math] period of lunar node precession = 18.613 years
  • [math]1/f_5=[/math] period of Earth's perihelion precession = 20940 years

(perigee = point in the Moon's elliptical orbit nearest to the earth, lunar nodes = points at which the Moon's orbit cuts the ecliptic, perihelion precession = drift of Earth's closest approach to the Sun)

This article considers the effect of the lunar node cycle and the lunar perigee cycle on ocean's tides. The effect of shorter periods of the Earth's and Moon's orbital motion is discussed in the article Ocean and shelf tides.


The 18.6-year lunar node cycle

The lunar node cycle refers to the precession of the Moon's orbital plane, where the lunar nodes complete one revolution in about 18.6 years. The lunar node cycle produces an 18.6-year oscillation of the lunar orbit relative to the equatorial plane. The declination (angle between lunar orbital plane and Earth's equatorial plane) varies between 18 and 28 degrees.

The primary driving force behind tidal motion on Earth is the gravitational pull exerted by the Moon. In a simplified model of an Earth without continents, the interaction between the Moon's gravity and the centrifugal acceleration resulting from Earth's orbit around the center of gravity of the Earth-Moon system creates two bulges on the ocean surface. One bulge is directed towards the Moon, while the other bulge is directed away from it (see Figure 1).

The Moon's orbital plane is inclined at an angle of approximately 5 degrees to the ecliptic plane (which is Earth's orbital plane around the Sun). On the other hand, the Earth's equatorial plane is inclined at an angle of around 23 degrees to the ecliptic plane. The angle between the Moon's orbital plane and Earth's equatorial plane, known as the Moon's declination, is not constant. It varies due to the precession of the Moon's axis, also referred to as lunar node precession.

The lunar node cycle (precession cycle) takes approximately 18.6 years to complete. Consequently, the Moon's declination ranges between a maximum of approximately 28 degrees (23 + 5) and a minimum of approximately 18 degrees (23 - 5).


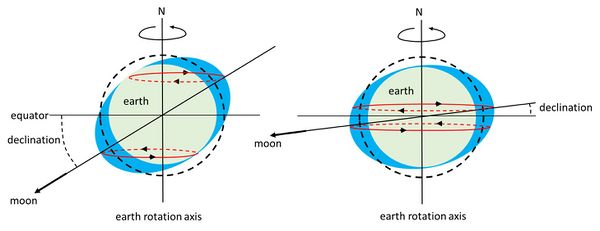
Fig. 1. Schematic of tide generation for different (exaggerated) Moon declinations. The Earth surface takes an oval shape due to the lunar gravitational force, with bulges along the Earth-Moon axis (strongly exaggerated). Left panel: For a large declination, a bulge passes through each point of the corresponding high latitudinal contour once a day, due to Earth’s rotation. Right panel: For a small declination, a bulge passes through each point of a low latitudinal contour twice a day. The rotation in the latitudinal planes is indicated in red.


Modulation of semidiurnal and diurnal tides

When the lunar declination is small, the semidiurnal tide is strong. During this phase of the lunar node cycle, the two high-water bulges formed by the combined effects of lunar gravity and Earth's centrifugal acceleration are located close to the equatorial plane. As a result, Earth's rotation produces two similar tidal pulses approximately every 25 hours (24 hours plus the Moon's progression time) along latitudinal contours near the equator.

On the other hand, when the lunar declination is large, the water bulges during the Moon's revolution around the Earth are situated, on average, farther away from the equator. As Earth rotates, this configuration leads to a tidal signal that exhibits a significant diurnal (25-hour) component. Figure 1 provides a schematic representation of these two opposite phases of the lunar precession, where it should be noted that the illustration is exaggerated for clarity.

Consequently, both the semidiurnal tide and the diurnal tide reach their maximum levels once during the lunar node cycle, which spans approximately 18.6 years. The time interval between these two phases is about 9.3 years, as shown in Figure 2.

Observed modulation of the semidiurnal and diurnal tidal amplitudes

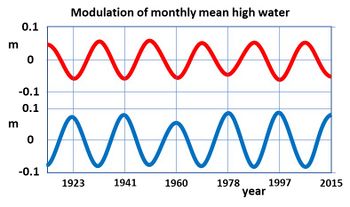
Fig. 2. Modulation of the monthly mean high water by the lunar node cycle. Blue curve: Case of semidiurnal tidal dominance (e.g. Brest, France). Red curve: Case of diurnal dominance (e.g. Victoria, Canada). Adapted from Peng et al. (2019[1]).


The idealized model of tide generation on an Earth without continents, the so-called equilibrium tide, does not accurately represent the actual tide generation process, which is influenced by the intricate topography of continental shelves. The strength of tidal motion in different locations on Earth is 4 determined not only by the intensity of the lunar tidal force but also by the resonance and dissipation processes of tidal motion resulting from topographic features.

The lunar node cycle modulates the tidal amplitudes, leading to variations ranging from 1 cm to 30 cm depending on the specific location[1]. In relative terms, the diurnal components experience stronger modulation compared to the semidiurnal components. On average, the semidiurnal M2 tide is modulated by about 3-4%, while the diurnal tides O1 and K1 are modulated by approximately 11% and 19%, respectively[2]). As the semidiurnal tide tends to be larger than the diurnal tide in most ocean regions, the modulation exhibits a similar magnitude for both the semidiurnal and diurnal tidal components.

The impact of the lunar node cycle on high-water levels is most pronounced in regions such as the English Channel, the Bristol Channel (both dominated by semidiurnal tides), and the Gulf of Tonkin (dominated by diurnal tides).

Impact of the lunar node cycle on coastal and marine processes

The lunar node cycle influences coastal processes that are regulated or modulated by tides. Because of the long periodicity, the influence of the lunar node cycle is easily confused with a change in long term trends. The influence of the lunar nodal tide on various coastal processes is discussed below.

Flooding risk

When heavy storms coincide with spring tidal high water, storm surge levels can be increased by a few centimeters up to a few tens of centimeters depending on the phase of the lunar declination. This should be reflected in the design conditions of coastal flood defenses in regions where the influence of the lunar node cycle on water level extremes is strong[1].

Cooling and warming of ocean surface waters

An analysis of long-term records of sea surface temperatures in North American waters reveals a recurring cycle of approximately 19 years. Locations along the East Coast, which are primarily influenced by the semidiurnal tide, experience temperature minima during years of minimum lunar declination. In contrast, locations along the West Coast, dominated by diurnal tides, observe temperature minima during years of maximum lunar declination[3].

This pattern can be attributed to increased tidal amplitudes during specific phases of the lunar node cycle, which enhance tidally induced mixing between warm surface waters and cooler deeper waters within the ocean thermocline. Numerical simulations conducted using a coupled ocean-atmosphere global circulation model validate this explanation[4]. These simulations further demonstrate that the 18.6-year cycle of cooling and warming of ocean surface waters has implications for the uptake of heat from the atmosphere and the overall response to global warming caused by greenhouse gas emissions[5].

Sediment deposition

Observations on the South American muddy coast, spanning 1500 km between the Amazon and Orinoco rivers, over the past twenty years reveal cycles of multiannual shoreline advance (progradation) and retreat (transgression). These cycles appear to be primarily influenced by the lunar 18.6-year node cycle. During the phase of minimum lunar declination, corresponding to increased tidal high waters, the shoreline tends to retreat. Conversely, during the phase of maximum lunar declination, the shoreline shows progradation. The long-term fluctuation of extreme tidal levels of about 6 cm induced by the lunar node cycle dominates over sea-level fluctuations from global warming or Niño-Niña events, and therefore provides a plausible explanation of the observed multiannual shoreline fluctuation[6].

Tidal basin morphology

The strength of sediment transport in coastal environments depends on the intensity of the current, with the relationship typically following a power law between 3 and 5 (see Sediment transport formulas for the coastal environment). As peak tidal currents are modulated by the lunar node cycle to a similar extent as peak tidal amplitudes, the modulation of peak sediment transport is typically three to five times greater. Depending on the phase of the lunar node cycle, the maximum tide-induced sediment transport can be increased or decreased by up to 10%.

Observations have identified an 18.6-year cycle in the infill of the Wadden Sea tidal basins, indicating the influence of the lunar node cycle on sedimentation[7]. Similarly, the volume of the Humber estuary has shown an 18.6-year cycle[8]. Historic sedimentation records in shallow tidal seas, such as the Santa Barbara Basin, also exhibit cycles with a periodicity close to 18.6 years[9]. Furthermore, a dataset spanning 68 years has revealed that tidal channels in the Baie du Mont-Saint-Michel undergo alternating configurations over periods close to 18.6 years[10].

Mangrove expansion and contraction

Observations indicate that the coverage of mangrove canopies along the Australian coastline increases or decreases based on the frequency and duration of inundation. Large parts of the gently sloping mudflats occupied by mangroves are only inundated when the tidal amplitude is sufficiently large. Since the 18.6-year lunar node cycle modulates the maximum tide levels, it thus influences the mangrove cover along the coast, in accordance with the observations[11]. Some coastal regions of Australia are dominated by semidiurnal tides and others by diurnal tides. The mangrove cover of these different regions shows contrasting multiannual fluctuations which are in line with the opposite phases of tidal amplitude modulation by the 18.6-year lunar node cycle.

El-Nino and Southern Oscillation

Statistical evidence from time series analysis suggests a potential link between the 18.6-year tidal node cycle and the El-Nino Southern Oscillation (ENSO) phenomenon[12]. The specific mechanisms by which this lunar cycle influences ENSO are not yet fully understood, but one proposed mechanism is the enhancement of tide-induced vertical mixing. However, further investigation is required to confirm and clarify the relationship between the 18.6-year tidal node cycle and ENSO.

Lunar nodal tide and mean sea level variation

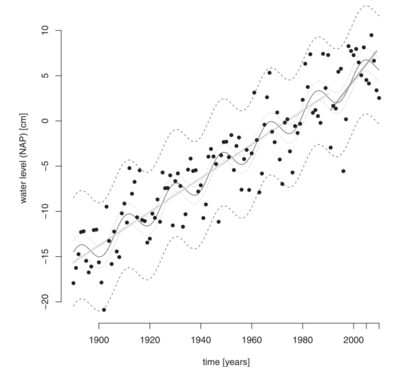
Fig. 3. Annual mean sea level averaged over six Dutch tidal stations (black dots). The modulation of the long-term linear trend represents the effect of the lunar nodal tide. The dotted lines represent confidence intervals. The linear fit at the end ignores the nodal tide and therefore overestimates the long-term trend. From Baart (2012[13]).

The gravitational pull exerted by the Moon on Earth, along with Earth's associated centrifugal acceleration, alters the shape of the ocean surface, as depicted in Fig. 1. This results in regions where the sea level is on average elevated (around the equator) and other regions where it is decreased (around the poles). The specific areas of increased and decreased ocean surface elevation fluctuate according to the Moon's declination. This fluctuation gives rise to a sea level oscillation known as the lunar nodal tide, with a period of 18.6 years, see Appendix. It is important to note that this lunar nodal tide should not be confused with the previously discussed 18.6-year modulation observed in the semidiurnal and diurnal tides. The amplitude of the lunar nodal tide is generally less than 1 cm, which is an order of magnitude smaller than the effect of the nodal tide on the semidiurnal and diurnal tidal amplitudes and on Mean High High Water (MHHW)[14].

Sea level changes due to the lunar node tide can amount to a few tenths of millimeters per year, which is significant compared to the sea level rise due to global warming. These changes can lead to local over- or underestimated long-term trends in sea level, and therefore should be considered when analyzing observational records to detect possible trend breaks[13]. While there are arguments suggesting that the theoretical equilibrium tide should adequately represent the lunar nodal tide[15], analyses of tide gauge records question this assumption[13][14][16]. Woodworth (2012[17]) identified several potential causes for departures from equilibrium theory but determining the best method to correct for the effect of the nodal tide on the mean sea level is still a topic of ongoing discussion.


The 8.8-year lunar perigee cycle

The semidiurnal and diurnal tides are modulated also by another long-period lunar cycle, the 8.8-year cycle related to the elliptical orbit of the Moon. During each revolution of about 27 days the Moon is sometimes closer to the Earth and sometimes further away. Moon's position closest to the Earth is called the perigee. The tidal forcing is strongest when the perigee is aligned with the Earth-Sun axis (leading to perigean spring tide), which occurs approximately twice a year. The strength of the semidiurnal tide also depends on the declination of the Sun, the angle of the Earth-Sun axis with the equatorial plane. The semidiurnal tide is strongest when the angle is zero, which occurs twice a year at equinox. Because the major axis of the Moon's elliptical orbit rotates 360o in about 8.8 years, the equinox coincides with the perigean spring tide once every about 4.4 years. Thus, the semidiurnal tide not only has a modulation of 18.6 years, but also a modulation of 4.4 years related to the moon's 8.8-year perigee cycle[18][19]. The 4.4-year modulation of the semidiurnal tide is generally subordinate to the 18.6-year modulation. A 4.4-year modulation also exists in the diurnal tidal components (O1, K1). This small modulation is related to phase coincidence of the lunar perigee with the maximum declination of the sun.


Appendix

The equilibrium theory of tides, taking into account the solid Earth elastic response, self-attraction and mass conservation, gives the following estimate for amplitude of the 18.6-year nodal tide[17]: [math]\quad a \approx 7 \; | 3 \, \sin^2 \theta - 1|, \quad[/math] where [math]a[/math] is the amplitude in mm and [math]\theta[/math] the latitude in radians. The amplitude is maximum at the poles and zero at 35 degrees N/S. High (> 35o) and low (< 35o) latitudes are out-of-phase; the phase at the equator corresponds to the phase of the nodal modulation of the semidiurnal tide.


Related articles

Ocean and shelf tides


Further reading

A physical and mathematical introduction useful for courses on tides and suited to researchers and engineers: Gerkema, T. 2019. An introduction to tides. Cambridge University Press, 222 pp.


References

  1. ↑ 1.0 1.1 1.2 Peng, D., Hill, E. M., Meltzner, A. J. and Switzer, A. D. 2019. Tide gauge records show that the 18.61‐year node tidal cycle can change high water levels by up to 30 cm. Journal of Geophysical Research: Oceans 124: 736–749 Cite error: Invalid <ref> tag; name "P19" defined multiple times with different content
  2. ↑ Godin, G. 1972. The Analysis of Tides. University of Toronto Press, Ontario
  3. ↑ Loder, J. W. and Garrett, C. 1978. The 18.6-Year Cycle of Sea Surface Temperature in Shallow Seas. J. Geophys. Res. 83: 1967-1970
  4. ↑ Joshi, M., Hall, R., Stevens, D. and Hawkins, E. 2022. The modelled climatic response to the 18.6-year lunar node cycle and its role in decadal temperature trends, EGUsphere [preprint], https://doi.org/10.5194/egusphere-2022-151
  5. ↑ Loder, J. W. and Garrett, C. 1978. The 18.6-Year Cycle of Sea Surface Temperature in Shallow Seas. J. Geophys. Res. 83: 1967-1970
  6. ↑ Gratiot, N., Anthony, E. J., Gardel, A., Gaucherel, C., Proisy, C. and Wells, J. 2008. Significant contribution of the 18.6 year tidal cycle to regional coastal changes. Nature Geoscience 1: 169–172
  7. ↑ Oost, A.P., de Haas, H., Ijnsen, F., van den Boogert, J.M. and de Boer, P.L., 1993. The 18,6 yr nodal cycle and its impact on tidal sedimentation. Sedimentary Geology 87: 1–11
  8. ↑ Wang, Z.B. and Townend, I.H. 2012. Influence of the nodal tide on the morphological response of estuaries. Marine Geology 291-294: 73–82
  9. ↑ Berger, W., Schimmelmann, A. and Lange, C. 2004. Tidal cycles in the sediments of Santa Barbara Basin. Geology 32: 329–332
  10. ↑ Levoy, F., Anthony, E.J., Dronkers, J., Monfort, O., Izabel, G. and Larsonneur, C. 2017. Influence of the 18.6-year lunar nodal tidal cycle on tidal flats: Mont-Saint-Michel Bay, France. Marine Geology 387: 108-113
  11. ↑ Saintilan, N., Lymburner, L., Wen, L., Haigh, I.D., Ai, E., Kelleway, J.L., Rogers, K., Pham, T.D. and Lucas, L. 2022. The lunar nodal cycle controls mangrove canopy cover on the Australian continent. Science Advances 8, eabo6602
  12. ↑ Yasuda, I. 2018. Impact of the astronomical lunar 18.6-yr tidal cycle on El-Niño and Southern Oscillation. Sci. Rep. 8, 15206
  13. ↑ 13.0 13.1 13.2 Baart, F., van Gelder, P. H. A. J. M., de Ronde, J., van Koningsveld, M. and Wouters C. 2012. The Effect of the 18.6-Year Lunar Nodal Cycle on Regional Sea-Level Rise Estimates, J. Coast. Res. 28: 511-516
  14. ↑ 14.0 14.1 Cherniawsky, J. Y., Foreman, M. G., Kang, S. K., Scharroo, R. and Eert, A. J. 2010. 18.6‐year lunar nodal tides from altimeter data. Continental Shelf Research 30: 575–587
  15. ↑ Proudman, J. 1960. The condition that a long-period tide shall follow the equilibrium law. Geophysical Journal of the Royal Astronomical Society 3: 244–249
  16. ↑ Hagen, R., Plüß, A., Jänicke, L., Freund, J., Jensen, J. and Kösters, F. 2021. A combined modeling and measurement approach to assess the nodal tide modulation in the North Sea. Journal of Geophysical Research Oceans 126, e2020JC016364
  17. ↑ 17.0 17.1 Woodworth, P. L. 2012. A note on the nodal tide in sea level records. Journal of Coastal Research 28: 316-323
  18. ↑ Ray, R. D. and Merrifield, M. A. 2019. The semiannual and 4.4-year modulations of extreme high tides. Journal of Geophysical Research: Oceans 124: 5907–5922
  19. ↑ Haigh, I., Elliot, M. and Pattiaratchi, C. 2011. Global influence of the 18.6-year nodal cycle and 8.85-year cycle of lunar perigee on high tide levels. Journal of Geophysical Research 116, C06025


The main authors of this article are Job Dronkers and Fedor Baart
Please note that others may also have edited the contents of this article.
Citation: Job Dronkers; Fedor Baart; (2023): Long-period lunar tides. Available from http://www.coastalwiki.org/wiki/Long-period_lunar_tides [accessed on 25-11-2024]
Retrieved from "https://www.coastalwiki.org/w/index.php?title=Long-period_lunar_tides&oldid=80311"