Difference between revisions of "Wave set-up"
Dronkers J (talk | contribs) |
Dronkers J (talk | contribs) |
||
| Line 13: | Line 13: | ||
<math>\eta_u \approx -\frac{\gamma}{16} H_b , \qquad \eta_u \approx \eta_d +\frac{3 \gamma}{8} H_b \approx \frac{5 \gamma}{16} H_b, \qquad (1)</math> | <math>\eta_u \approx -\frac{\gamma}{16} H_b , \qquad \eta_u \approx \eta_d +\frac{3 \gamma}{8} H_b \approx \frac{5 \gamma}{16} H_b, \qquad (1)</math> | ||
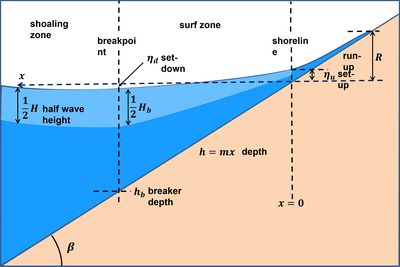
| − | where <math>\gamma = H_b/h_b</math> is the [[breaker index]] (values in the range 0.5-1.2), <math>H_b</math> is the wave height at the breakpoint and <math>h_b</math> the depth at the breakpoint (see Fig. 1) | + | where <math>\gamma = H_b/h_b</math> is the [[breaker index]] (values in the range 0.5-1.2), <math>H_b</math> is the wave height at the breakpoint and <math>h_b</math> the depth at the breakpoint (see Fig. 1). |
| − | Besides monochromatic waves and applicability of shallow-water wave theory, other assumptions are: | + | The numerous assumptions underlying Eq. (1) limit its practical usefulness. Besides monochromatic waves and applicability of shallow-water wave theory, other assumptions are: |
* a constant shoreface seabed slope <math>m = \tan\beta</math>, i.e. depth <math>h(x) = m \, x</math>; | * a constant shoreface seabed slope <math>m = \tan\beta</math>, i.e. depth <math>h(x) = m \, x</math>; | ||
* shallow water, <math>2kh_b < 1</math> (<math>k=2 \pi / L</math> is the wave number); | * shallow water, <math>2kh_b < 1</math> (<math>k=2 \pi / L</math> is the wave number); | ||
| Line 22: | Line 22: | ||
* roller energy of breaking waves can be ignored; | * roller energy of breaking waves can be ignored; | ||
* no momentum loss through dissipation at the seabed. | * no momentum loss through dissipation at the seabed. | ||
| + | Numerical modeling shows that neglecting momentum dissipation at the seabed (mainly momentum dissipation related to the undertow current) yields an underprediction of the wave set-up<ref> Apotsos, A., Raubenheimer, B., Elgar, S., Guza, R.T. and Smith, J.A. 2007. Effects of wave rollers and bottom stress on wave setup. J. Geophysical Research 112, C02003</ref>. | ||
| − | + | In practice, empirical formulas derived from field and laboratory measurements are often used for determining the wave set-up. Many different formulas can be found in the literature<ref>Gomes da Silva, P., Coco, G., Garnier, R. and Klein, A.H.F. 2020. On the prediction of runup, setup and swash on beaches. Earth-Science Reviews 204, 103148</ref>. Most of these formulas relate the wave set-up to the offshore significant wave height <math>H_s</math>, the deep-water wave length <math>L = g T^2 \ /2 \pi</math> and the average surf zone bed slope <math>m=\tan \beta</math>. | |
| − | + | Several field measurements <ref>Guza, R.T. and Thornton, E.B. 1981. Wave set-up on a natural beach. J. Geophys. Res. 86: 4133–4137</ref><ref name=R1>Raubenheimer, B., Guza, R.T.and Elgar, S. 2001. Field observations of wave-driven setdown and setup. J. Geophys. Res. 106: 4629–4638</ref><ref>Atkinson, A. L., Power, H. E., Moura, T., Hammond, T., Callaghan, D. P. and Baldock, T. E. 2017. Assessment of runup predictions by empirical models on non‐truncated beaches on the south‐east Australian coast. Coastal Engineering 119: 15–31</ref> report values compatible with Eq. (1): | |
| − | <math>\eta_u = C \, | + | <math>\eta_u \approx 0.16 H_s, \qquad (2)</math> |
| + | |||
| + | where <math>H_s</math> is the significant offshore wave height. | ||
| + | |||
| + | A popular formula for the wave set-up is<ref>Holman, R.A. and Sallenger, A.H. 1985. Setup and swash on a natural beach. J. Geophys. Res. 90: 945–953</ref><ref>Stockdon, H.F., Holman, R.A., Howd, P.A. and Sallenger, A.H. 2006. Empirical parameterization of setup, swash, and runup. Coast. Eng. 53: 573–588</ref><ref>Medellín, G., Brinkkemper, J.A., Torres-Freyermuth, A., Appendini, C.M., Mendoza, E.T. and Salles, P. 2016. Run-up parameterization and beach vulnerability assessment on a barrier island: a downscaling approach. Nat. Hazards Earth Syst. Sci. 16: 167–180</ref> | ||
| + | |||
| + | <math>\eta_u= C \, H_s \, \xi = C \, m \, \sqrt{H_s\, L}, \qquad (3)</math> | ||
| − | where <math>\xi=m/ \sqrt{ | + | where <math>\xi=m/ \sqrt{H_s/L}</math> is the [[surf similarity parameter]] . The constant <math>C</math> can take values in the range 0.15 – 0.4. |
| − | Other empirical formulas differ from Eq. ( | + | Other empirical formulas differ from Eq. (3) especially regarding the dependence on the surf zone slope <math>m</math>, either by no dependence on <math>m</math><ref>Hanslow, D.J. and Nielsen, P. 1992. Wave setup on beaches and in river entrances. In: Proc. of the 23rd International Conference on Coastal Engineering. Venice, Italy, pp. 240–252</ref> or by an inverse relationship with <math>m</math><ref name=R1>Raubenheimer, B., Guza, R.T. and Elgar, S. 2001. Field observations of wave-driven setdown and setup. J. Geophys. Res. 106: 4629–4638</ref><ref>Didier, D., Caulet, C., Bandet, M., Bernatchez, P., Dumont, D., Augereau, E., Floc’h, F. and Delacourt, C. 2020. Wave runup parameterization for sandy, gravel and platform beaches in a fetch-limited, large estuarine system. Continental Shelf Research 192: 104024</ref>. |
The great diversity of empirical formulas and associated values for the wave set-up illustrates the limitations inherent to simple parameterizations of the shoreface. The shoreface bathymetry is highly variable and differs greatly among coasts, even among nearby locations. Complex bathymetries are ubiquitous due to the presence of [[nearshore sandbars]] and other [[rhythmic shoreline features]]. Accurate estimates of the wave set-up require in-situ observations or detailed numerical models. | The great diversity of empirical formulas and associated values for the wave set-up illustrates the limitations inherent to simple parameterizations of the shoreface. The shoreface bathymetry is highly variable and differs greatly among coasts, even among nearby locations. Complex bathymetries are ubiquitous due to the presence of [[nearshore sandbars]] and other [[rhythmic shoreline features]]. Accurate estimates of the wave set-up require in-situ observations or detailed numerical models. | ||
Revision as of 17:30, 16 April 2023
Definition of Wave set-up:
Elevation of the mean water level at the shoreline due to wave breaking in the surf zone.
This is the common definition for Wave set-up, other definitions can be discussed in the article
|
Notes
Wave transformation in shallow water generates changes in the mean water level, called set-up for an upward change and set-down for a downward change. The changes in mean sea level are related to the so-called radiation stress. The radiation stress is defined as the flow of momentum due to wave orbital motions. Gradients in the radiation stress induce an effective momentum transfer from wave motion to steady motion that takes place when the wave amplitude changes along the direction of propagation (see for further explanations Shallow-water wave theory#Radiation Stress (Momentum Flux)). Wave set-down [math]\eta_d[/math] occurs in the shoaling zone where the wave amplitude increases; wave wet-up [math]\eta_u[/math] occurs in the surf zone where the wave amplitude decreases. Analytical expressions of the wave set-down at the breakpoint and the wave set-up at the shoreline can be derived for a monochromatic wave, see Shallow-water wave theory#Wave set-down and set-up:
[math]\eta_u \approx -\frac{\gamma}{16} H_b , \qquad \eta_u \approx \eta_d +\frac{3 \gamma}{8} H_b \approx \frac{5 \gamma}{16} H_b, \qquad (1)[/math]
where [math]\gamma = H_b/h_b[/math] is the breaker index (values in the range 0.5-1.2), [math]H_b[/math] is the wave height at the breakpoint and [math]h_b[/math] the depth at the breakpoint (see Fig. 1).
The numerous assumptions underlying Eq. (1) limit its practical usefulness. Besides monochromatic waves and applicability of shallow-water wave theory, other assumptions are:
- a constant shoreface seabed slope [math]m = \tan\beta[/math], i.e. depth [math]h(x) = m \, x[/math];
- shallow water, [math]2kh_b \lt 1[/math] ([math]k=2 \pi / L[/math] is the wave number);
- depth-limited wave amplitude [math]H/h=\gamma \;[/math] throughout the surf zone (saturated wave breaking);
- wave skewness and asymmetry can be ignored;
- roller energy of breaking waves can be ignored;
- no momentum loss through dissipation at the seabed.
Numerical modeling shows that neglecting momentum dissipation at the seabed (mainly momentum dissipation related to the undertow current) yields an underprediction of the wave set-up[1].
In practice, empirical formulas derived from field and laboratory measurements are often used for determining the wave set-up. Many different formulas can be found in the literature[2]. Most of these formulas relate the wave set-up to the offshore significant wave height [math]H_s[/math], the deep-water wave length [math]L = g T^2 \ /2 \pi[/math] and the average surf zone bed slope [math]m=\tan \beta[/math].
Several field measurements [3][4][5] report values compatible with Eq. (1):
[math]\eta_u \approx 0.16 H_s, \qquad (2)[/math]
where [math]H_s[/math] is the significant offshore wave height.
A popular formula for the wave set-up is[6][7][8]
[math]\eta_u= C \, H_s \, \xi = C \, m \, \sqrt{H_s\, L}, \qquad (3)[/math]
where [math]\xi=m/ \sqrt{H_s/L}[/math] is the surf similarity parameter . The constant [math]C[/math] can take values in the range 0.15 – 0.4.
Other empirical formulas differ from Eq. (3) especially regarding the dependence on the surf zone slope [math]m[/math], either by no dependence on [math]m[/math][9] or by an inverse relationship with [math]m[/math][4][10].
The great diversity of empirical formulas and associated values for the wave set-up illustrates the limitations inherent to simple parameterizations of the shoreface. The shoreface bathymetry is highly variable and differs greatly among coasts, even among nearby locations. Complex bathymetries are ubiquitous due to the presence of nearshore sandbars and other rhythmic shoreline features. Accurate estimates of the wave set-up require in-situ observations or detailed numerical models.
Related articles
References
- ↑ Apotsos, A., Raubenheimer, B., Elgar, S., Guza, R.T. and Smith, J.A. 2007. Effects of wave rollers and bottom stress on wave setup. J. Geophysical Research 112, C02003
- ↑ Gomes da Silva, P., Coco, G., Garnier, R. and Klein, A.H.F. 2020. On the prediction of runup, setup and swash on beaches. Earth-Science Reviews 204, 103148
- ↑ Guza, R.T. and Thornton, E.B. 1981. Wave set-up on a natural beach. J. Geophys. Res. 86: 4133–4137
- ↑ 4.0 4.1 Raubenheimer, B., Guza, R.T.and Elgar, S. 2001. Field observations of wave-driven setdown and setup. J. Geophys. Res. 106: 4629–4638 Cite error: Invalid
<ref>tag; name "R1" defined multiple times with different content - ↑ Atkinson, A. L., Power, H. E., Moura, T., Hammond, T., Callaghan, D. P. and Baldock, T. E. 2017. Assessment of runup predictions by empirical models on non‐truncated beaches on the south‐east Australian coast. Coastal Engineering 119: 15–31
- ↑ Holman, R.A. and Sallenger, A.H. 1985. Setup and swash on a natural beach. J. Geophys. Res. 90: 945–953
- ↑ Stockdon, H.F., Holman, R.A., Howd, P.A. and Sallenger, A.H. 2006. Empirical parameterization of setup, swash, and runup. Coast. Eng. 53: 573–588
- ↑ Medellín, G., Brinkkemper, J.A., Torres-Freyermuth, A., Appendini, C.M., Mendoza, E.T. and Salles, P. 2016. Run-up parameterization and beach vulnerability assessment on a barrier island: a downscaling approach. Nat. Hazards Earth Syst. Sci. 16: 167–180
- ↑ Hanslow, D.J. and Nielsen, P. 1992. Wave setup on beaches and in river entrances. In: Proc. of the 23rd International Conference on Coastal Engineering. Venice, Italy, pp. 240–252
- ↑ Didier, D., Caulet, C., Bandet, M., Bernatchez, P., Dumont, D., Augereau, E., Floc’h, F. and Delacourt, C. 2020. Wave runup parameterization for sandy, gravel and platform beaches in a fetch-limited, large estuarine system. Continental Shelf Research 192: 104024