Wave loading on coastal structures

Coastal structures, such as seawalls and breakwaters, are exposed to two types of wave impacts. On the one hand, waves exert an overall force on the structure through the wave-pressure distribution. On the other hand, steep or breaking waves can generate a local impulsive force when the wave front hits the structure. The first type of impact does not strongly depend on the wave shape, see e.g. Shallow-water wave theory#Vertical Walls. The second impact type, in contrast, is much stronger for steep asymmetric waves than for sinusoidal waves. Gentle, regular waves are reflected at the structure creating a standing wave pattern, whereas steep waves can generate violent fluid motions and associated pressures when they collide with the structure. The structure of the wall (smooth, rough, perforated, block work, sloping or curved) also influences in this case the impact of a wave. The pressure-impulse impact is highly variable, as it strongly depends on the shape of the wave just before hitting the structure. The pressure peak is concentrated in a small area around the still water level. Since the impact is localized, it generally does not affect the structure stability as a whole, but it can cause important local damage.

Total wave pressure loading

Fig. 1. Goda’s formula for forward wave pressure loading on a vertical breakwater.

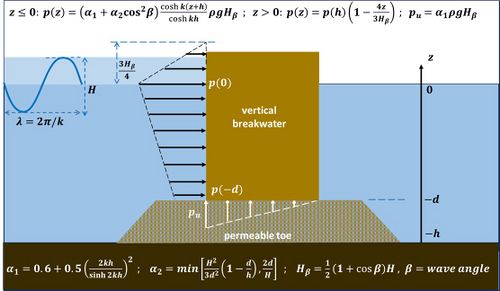
The Goda wave load formula gives an equivalent quasi-static wave-pressure distribution for the design of composite vertical breakwaters. It is used to assess failure mechanisms of caisson breakwaters, especially sliding and overturning. These loads are the main forces to consider for wind waves and swell of low to medium steepness reflecting from the vertical face of heavy monolithic structures. For such structures the slowly varying wave load is commonly treated as quasi-static in stability calculations, since their characteristic natural periods are much shorter than the periods of the incident waves. Goda's original wave load formula for the design wave height [math]H[/math] (highest wave in the design sea state just in front of the structure, often of the order [math]\sim 1.8 \, H_s[/math]) is shown in Fig. 1. It considers the (slowly) pulsating loads of both breaking and reflected waves and includes the effect of the wave incidence angle [math]\beta[/math]. The wave pressure on the front face is denoted by [math]p(z)[/math] and the uplift pressure by [math]p_u[/math]. They are almost triangularly distributed along the structure's front face and bottom. The uplift pressure represents the wave-induced pressure acting beneath the caisson, transmitted through water in the rubble mound or other permeable foundation material. It is much less relevant for nearly impermeable foundations such as stiff clay or fine, dense sand.

The maximum elevation to which pressure can be exerted is taken as [math]0.75 H[/math] above the still water level. Goda's formula has been refined later on by Takahashi et al. (1994) and other authors. See also the Coastal Engineering Manual (2012).

Fig. 2. Boccotti’s formula for seaward wave pressure loading on a vertical breakwater.

Under the wave trough, breakwaters are exposed to seaward wave loading. Field experiments by Boccotti (2000) have shown that this seaward wave loading can be very strong and can even exceed the maximum landward wave loading. The seaward pressure distribution and the associated formula are shown in Figure 2. For a design sea state with a given significant wave height [math]H_s[/math] just in front of the structure, the wave height [math]H^{(-)}[/math] corresponds to the deepest wave troughs statistically occurring with a certain low frequency. Boccotti et al. (2012) determined these virtual wave heights [math]H^{(-)}[/math] empirically for intermediate water depths ([math]d/L \sim 0.15-0.2[/math]) with the result: [math]H^{(-)} \approx 1.5 \, H_s[/math] for the average of the 10% deepest wave troughs, [math]H^{(-)} \approx 2 \, H_s[/math] for the 1% deepest troughs and [math]H^{(-)} \approx 2.3 \, H_s[/math] for the 1‰ deepest troughs. The weight of negative pressures becomes more important as water depth increases. For [math]d/L \sim 0.2-0.3[/math] the 1‰ deepest troughs correspond to [math]H^{(-)} \approx 3 \, H_s[/math]. This implies that the control of the overall stability under the action of negative wave forces becomes crucial in deep water ([math]d/L \gt 0.2[/math]).

It is prudent not to use empirical formulas for design purposes outside calibration ranges. Such formulas are often unsuitable for detailed local damage assessment or probabilistic safety factors without physical modelling or numerical modelling, see e.g. Hydrodynamic numerical models of wave-structure interaction.

Wave-impulse loading

A wave impulse is the momentum transferred from the advancing wave front to the structure. If the front of the incident wave steepens and becomes more or less vertical just before it reaches the vertical wall of a structure, the wave impulse impact can be very violent. For a given impulse, the peak pressure increases when the impact area and impact duration decrease. Impact durations are of the order of 10 to 100 milliseconds and peak pressures can reach up to 1 MPa. The impact process is closely linked to the shape of the breaking wave in front of the structure. The greatest water speed generated by a freely traveling water wave occurs when the crest of the wave overturns, generating a jet of water as the wave breaks. This jet of water traps an air pocket as it strikes the wall. A fraction of the compressed air pocket is released upwards with the wave splash while the remainder is collapsed into small air bubbles, see also Wave collision on a vertical wall. Breakaway of the air pocket results in a strong reduction of the peak pressure magnitude and generates a double-peaked pressure just below the impinging region. If the wave has already fully broken before the impact, the turbulent wave front consists of an air-water mixture when hitting the wall. The compressibility of the air increases the impact duration and so reduces the pressure impact. The cushion effect increases with the size of the entrapped air pocket, but very high peak pressures have been recorded for both small and large air pockets . Localized high-pressure events can also be disrupted by disturbances, for example if the structure has roughness elements that are small on the scale of the incident wave but have a size comparable to that of the peak pressure area. Based on large-scale flume tests, Cuomo et al. (2010) propose the following empirical formula for the impact force [math]F_{1/250}[/math] exerted by the mean of the 1/250 highest waves on a vertical structure per unit width,

[math]F_{1/250} = C_r^{1.65} \, \rho \, g \, H \, L \, \Big(1 - \dfrac{|h_b-h|}{h} \Big) \, . [/math]

Meaning of the symbols: [math]C_r=[/math] wave reflection coefficient of the structure (about 0.9 for vertical walls), [math]\rho=[/math] seawater density, [math]g=[/math] gravitational acceleration, [math]H=[/math] significant (spectral) wave height, [math]L=[/math] wavelength, [math]h=[/math] water depth at the toe of the structure, [math]h_b=[/math] breaker depth.

Flip-through wave impact

Fig. 3. Successive profiles of a wave approaching a wall from right to left, illustrating wave front steepening, rapid squeezing and filling of the wave trough, and generation of a jet climbing the rigid wall. This so-called ‘flip-through’ process creates a strong pressure peak near the still water level. Redrawn after Peregrine (2003).

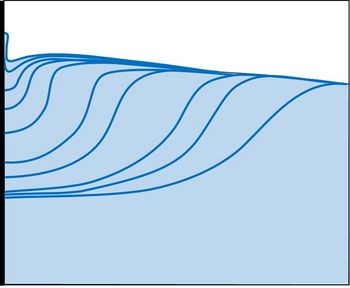
Flume experiments show that the steep front of a wave that propagates towards a solid wall will not always crash onto the wall as in the wave-impulse scenario. Instead, the wave trough ahead of the advancing wave crest is compressed against the wall and fills quickly as the wave front gets close. The water level in the wave trough rises so rapidly that a small jet is formed that climbs the wall in a split second before the wave front reaches the wall. This phenomenon, illustrated in Fig. 3, is called flip-through. The fast, vertical jet that emerges from a small high pressure region near the wall, implies that the violent flip-through occurs without any actual impact. Although the jet prevents the wave front from making direct contact with the wall, computations demonstrate that the resultant smooth flow can still generate very large localized pressures on the wall.

The flip-through phenomenon may occur at any rigid boundary over which the free surface moves because gravity is unimportant in this part of the flow, so the 'wall' need not be vertical. For example, flip-through can occur when non-breaking waves run up a beach of moderate slope and produce an uprush jet.

Dynamic response to impulsive wave loading

For massive coastal structures, wave loads with durations comparable to the wave period are often treated as quasi-static loads for stability calculations. This approximation is not always valid for impulsive breaking-wave impacts, whose rise time and duration can be much shorter than the incident-wave period and may excite structural or foundation vibrations. Whether this dynamic response is important depends on the natural period, damping, stiffness and support conditions of the particular structure; it is therefore usually assessed with structure-specific models or physical tests when impulsive loading is expected. This is particularly relevant for slender hydraulic structures such as sluices, navigation locks and storm-surge barriers, whose natural periods may be much longer than the duration of breaking-wave impacts. As a result, slender hydraulic structures typically have a quasi-static response to pulsating wave loads, and a dynamic response to breaking and impact wave loads. Goda (1994) showed that a rough indication of the dynamic response of a coastal structure to wave impulse loading can be obtained from a simplified model in which a coastal structure is represented by a system of mass and dual springs for rotational and horizontal motions.

Related articles

Wave collision on a vertical wall

Stability of rubble mound breakwaters and shore revetments

Shallow-water wave theory

Statistical description of wave parameters

Hydrodynamic numerical models of wave-structure interaction

References

The main author of this article is Job Dronkers Please note that others may also have edited the contents of this article. Citation: Job Dronkers (2026): Wave loading on coastal structures. Available from http://www.coastalwiki.org/wiki/Wave_loading_on_coastal_structures [accessed on 19-06-2026] For other articles by this author see Category:Articles by Job Dronkers For an overview of contributions by this author see Special:Contributions/Dronkers J