Difference between revisions of "Ocean and shelf tides"

From Coastal Wiki
Jump to: navigation, search
Line 5: Line 5:
 
==Introduction==  
 
==Introduction==  
  
−
Tidal motion is the oscillation of ocean waters under influence of the attractive gravitational forces of the moon and the sun. The response of the ocean to the gravitational forces follows a pattern of rotating ('amphidromic') systems, as a consequence of earth's rotation. The frequencies are determined by the relative periodic motions of moon, sun and earth surface. The amplitude of the tidal oscillation is very small compared to ocean depths. The ocean tidal oscillation in each point can therefore be represented by a linear superposition of sinusoidal tidal components with frequencies corresponding to the different cycles of the gravitational forces. The most important tidal components have a periodicity which is close to semidiurnal or diurnal, due to earth's rotation.
+
Tidal motion is the oscillation of ocean waters under the influence of the attractive gravitational forces of the moon and the sun. The response of the ocean to the gravitational forces follows a pattern of rotating ('amphidromic') systems, as a consequence of earth's rotation. The frequencies are determined by the relative periodic motions of moon, sun and earth surface. The amplitude of the tidal oscillation is very small compared to ocean depths. The ocean tidal oscillation in each point can therefore be represented by a linear superposition of sinusoidal tidal components with frequencies corresponding to the different cycles of the gravitational forces. The most important tidal components have a periodicity which is close to semidiurnal or diurnal, due to earth's rotation.  
−
 
 
−
This article is an adaptation of the sections on ocean tides from the book Dynamics of Coastal Systems <ref name=D>Dronkers, J. 2017. Dynamics of Coastal Systems. World Scientific Publ. Co., Advanced Series on Ocean Engineering, 740 pp.</ref>.
 
  
  
Line 13: Line 11:
  
 
===Moon and sun===
 
===Moon and sun===
−
The regular daily upward and downward motion of the water surface along the coastline is the most visible expression of tidal forcing. In ancient Greece it was recognized that tides are in some way related to sun and moon, but this relationship could not be explained <ref>Ekman, M. 1993. A concise history of the theories of tides, precession-nutation and polar motion. Surveys in Geophysics 14: 585-617</ref>. The explanation of tidal motion as a consequence of gravitational forces was given by Newton. The lunar and solar tide generating forces acting on the oceans are extremely small; they are about a factor <math>\, 10^{-7} \,</math> smaller than the gravitational force of the earth. The tide-generating force of the moon is about twice as large as that of the sun.
+
The regular daily upward and downward motion of the water surface along the coastline is the most visible expression of tidal forcing. In ancient Greece it was recognized that tides are in some way related to sun and moon, but this relationship could not be explained <ref>Ekman, M. 1993. A concise history of the theories of tides, precession-nutation and polar motion. Surveys in Geophysics 14: 585-617</ref>. The explanation of tidal motion as resulting from gravitational forces was given by Newton. The lunar and solar tide generating forces acting on the oceans are extremely small; they are about a factor <math>\, 10^{-7} \,</math> smaller than the gravitational force of the earth. The tide-generating force of the moon is about twice as large as that of the sun.
  
 
===Tidal wave and ocean basin resonance===
 
===Tidal wave and ocean basin resonance===
−
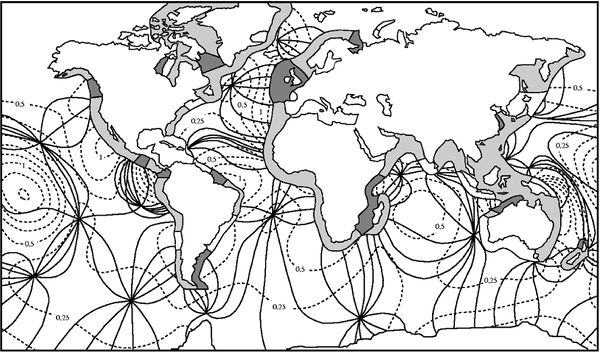
Ocean tides owe their strength for a large part to resonance; tidal motion is amplified for tidal components with a frequency close to the frequency of free oscillations in the ocean basins. This is the case in particular for the semi-diurnal tide in the North Atlantic and Pacific Oceans <ref> Heath, R.A. 1981. Estimates of the resonant period and Q in the semi-diurnal tidal band in the North Atlantic and Pacific Oceans. Deep-Sea Research. Vol. 28A: 481 – 493</ref>, and also for the diurnal tide in the Pacific ocean <ref> Müller, M. 2007. The free oscillations of the world ocean in the period range 8 to 165 hours including the full loading effect. Geophys. Res. Letters 34, L05606, doi:10.1029/2006GL028870, 2007</ref>. Tidal waves in wide ocean basins (width typically larger than a few thousand km) rotate around points of zero amplitude, the amphidromic points; the rotation is counterclockwise in the Northern Hemisphere and clockwise in the Southern Hemisphere. This due to earth's rotation, which induces [[Coriolis acceleration]] of tidal currents. Fig.1 shows the semi-diurnal tidal wave in the world's oceans; it comprises a large number of amphidromic systems, where the tide rotates in resonance with the semi-diurnal component of the gravitational force. This ocean tidal wave pattern can be described in first approximation by a combination of Kelvin and Sverdrup waves (also called Poincaré waves, see [[Tidal motion in shelf seas]]).
+
Ocean tides owe their strength for a large part to resonance; tidal motion is amplified for tidal components with a frequency close to the frequency of free oscillations in the ocean basins. This is the case in particular for the semi-diurnal tide in the North Atlantic and Pacific Oceans <ref> Heath, R.A. 1981. Estimates of the resonant period and Q in the semi-diurnal tidal band in the North Atlantic and Pacific Oceans. Deep-Sea Research. Vol. 28A: 481 – 493</ref>, and also for the diurnal tide in the Pacific Ocean <ref> Müller, M. 2007. The free oscillations of the world ocean in the period range 8 to 165 hours including the full loading effect. Geophys. Res. Letters 34, L05606, doi:10.1029/2006GL028870, 2007</ref>. Tidal waves in wide ocean basins (width typically larger than a few thousand km) rotate around points of zero amplitude, the amphidromic points; the rotation is counterclockwise in the Northern Hemisphere and clockwise in the Southern Hemisphere. This due to earth's rotation, which induces [[Coriolis acceleration]] of tidal currents. Fig.1 shows the semi-diurnal tidal wave in the world's oceans; it comprises a large number of amphidromic systems, where the tide rotates in resonance with the semi-diurnal component of the gravitational force. This ocean tidal wave pattern can be described in first approximation by a combination of [[Coriolis and tidal motion in shelf seas#Kelvin wave|Kelvin]] and Sverdrup waves (also called Poincaré waves, see [[Tidal motion in shelf seas]]).
 +
 
 +
 
 +
[[Image: worldtides.jpeg|thumb|center|600px|Fig. 1. System of semidiurnal lunar tidal waves (<math>M_2</math>) in the oceans represented by lines of equal tidal phase (solid, intervals of 30<math>^{\circ}</math>) and lines of equal tidal amplitude (dashed, intervals of 0.25 m). Three ranges are indicated for the tidal amplitude <math>a</math> on the continental shelf: microtidal (white fringe, <math>a < </math> 1 m), mesotidal (light grey fringe, 1 <math> < a < </math> 2 m) and macrotidal (dark grey fringe, <math>a > </math> 2 m). Redrawn after Bearman (1991) <ref> Bearman, G. (Ed.) 1991. Waves, tides and shallow-water processes. The Open University, Pergamon Press, Oxford</ref>]]
  
 +
===Tidal Energy Dissipation===
 +
The total power available from Moon and Sun on the global ocean is estimated at 3.7 TW (<math>10^{12}</math> Watts); after allowing for a comparatively small dissipation in the atmosphere and the solid Earth, 3.5 TW remain to be dissipated in the ocean (Munk and Wunsch, 1998)<ref name=MW>Munk, W. H. and Wunsch C. 1998. Abyssal recipes II: Energetics of tidal and wind mixing, Deep-Sea Research 45: 1977-2010</ref>. For comparison, the geothermal heat loss is 30 TW, and the equator-to-pole ocean heat-flow is 2,000 TW. Solar radiation input (175,000 TW) is five orders of magnitude greater than the tidal power.
  
−
[[Image: worldtides.jpeg|thumb|center|600px|Fig.1. System of semidiurnal lunar tidal waves (M2) in the oceans represented by lines of equal tidal phase (solid, intervals of 30<math>^{\circ}</math>) and lines of equal tidal amplitude (dashed, intervals of 0.25 m). Three ranges are indicated for the tidal amplitude <math>a</math> on the continental shelf: microtidal (white fringe, <math>a < </math> 1 m), mesotidal (light grey fringe, 1 <math> < a < </math> 2 m) and macrotidal (dark grey fringe, <math>a > </math> 2 m). Redrawn after Bearman (1991) <ref> Bearman, G. (Ed.) 1991. Waves, tides and shallow-water processes. 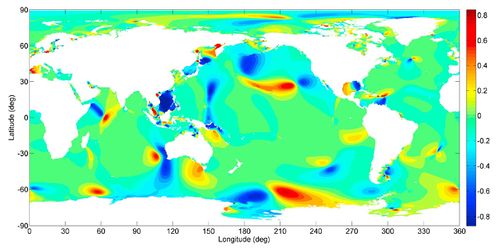The Open University, Pergamon Press, Oxford</ref>]]
+
[[Image:M2EnergyDissipation.jpg|thumb|right|500px|Fig. 2. Estimates of <math>M_2</math> tidal energy dissipation based on six years of altimeter data from the TOPEX/Poseidon satellite. The blue patches (negative dissipation) are clearly not physical, and provide some indication of the magnitude of noise in the estimates (Egbert and Ray, 2000)<ref>Egbert, G. D., and R. D. Ray (2000), Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data, Nature, 405, 775-778</ref>. Image from [https://eoimages.gsfc.nasa.gov/images/imagerecords/0/654/dissipation_large.jpg NASA]. ]]
 +
 
 +
The tidal energy dissipation due to the <math>M_2</math> tide can be exactly calculated from astronomic observation programs at 2.5 TW, of which 0.1 TW is dissipated in the atmosphere and the solid Earth (Munk, 1997)<ref name=M> Munk, W. H. 1997. Once again: once again–tidal friction, Progress in Oceanography 40: 7-35</ref>. It is estimated that 1.8 TW of <math>M_2</math> energy (2.5 TW of all lunar and solar constituents) is lost in the turbulent bottom boundary layers of marginal seas due to the work against bottom friction which opposes tidal currents. This kind of energy dissipation is concentrated in a few shelf areas of strong tidal current, such as the north-west European Shelf, the Patagonian Shelf, the Yellow Sea, the Timor and Arafura Seas, and the Amazon Shelf (Fig. 2). The other 0.6 TW of <math>M_2</math> tidal dissipation (1.0 TW of all lunar and solar constituents) occurs in the open ocean through the scattering by ocean-bottom topography of surface tides into internal tidal waves (Egbert and Ray, 2000). The breaking of internal waves may be concentrated in a few areas, generally near rugged bottom topography, for example seamounts and mid-ocean ridges (Fig. 2), and is believed to be a principal contributor to drive the ocean interior mixing (Munk and Wunsch, 1998)<ref name=MW></ref>.
  
 
===Modelling ocean tides===
 
===Modelling ocean tides===
 
Modelling ocean tides remains a challenge, even with modern fast computers. Because the tidal wavelength is much larger than ocean depth, these models are generally based on the hydrostatic shallow-water equations. Relatively simple models considering the response of a homogeneous ocean to the tide-generating forces yield results in qualitative agreement with observations. However, for better quantitative agreement stratification and internal tide generation (at ocean ridges, in particular) should be included. Other factors that need to be taken into account are:
 
Modelling ocean tides remains a challenge, even with modern fast computers. Because the tidal wavelength is much larger than ocean depth, these models are generally based on the hydrostatic shallow-water equations. Relatively simple models considering the response of a homogeneous ocean to the tide-generating forces yield results in qualitative agreement with observations. However, for better quantitative agreement stratification and internal tide generation (at ocean ridges, in particular) should be included. Other factors that need to be taken into account are:
−
*Tide-induced seafloor deformation under the weight of the water column;
+
*Tide-induced seafloor deformation under the weight of the water column (loading tide);
 
*Tide-induced seafloor deformation related to the solid earth tide;
 
*Tide-induced seafloor deformation related to the solid earth tide;
−
*Gravitational attraction induced by the mass of the ocean on the ocean itself.   
+
*Gravitational attraction induced by the mass of the ocean on the ocean itself (self-attraction).   
 
See Hendershott (2007)  <ref> Hendershott, M.C. 2007. Long Waves and Ocean Tides. In: Evolution of Physical Oceanography (Eds. B. Warren, and C. Wunsch) MIT OpenCourseWare, https://ocw.mit.edu </ref> for a discussion of these different factors.  
 
See Hendershott (2007)  <ref> Hendershott, M.C. 2007. Long Waves and Ocean Tides. In: Evolution of Physical Oceanography (Eds. B. Warren, and C. Wunsch) MIT OpenCourseWare, https://ocw.mit.edu </ref> for a discussion of these different factors.  
  
Line 37: Line 42:
 
Because the solar and lunar orbits do not coincide with the equatorial plane (the angle between orbital plane and equatorial plane is called declination), a daily inequality arises in the semidiurnal cycle. The daily inequality is strongest in shelf seas that resonate at diurnal frequency and which are situated close to amphodromic points of the semidiurnal tide. In such regions the tide is mainly diurnal.
 
Because the solar and lunar orbits do not coincide with the equatorial plane (the angle between orbital plane and equatorial plane is called declination), a daily inequality arises in the semidiurnal cycle. The daily inequality is strongest in shelf seas that resonate at diurnal frequency and which are situated close to amphodromic points of the semidiurnal tide. In such regions the tide is mainly diurnal.
  
−
Due to the <math>\approx</math> 30-day orbital motion of the moon, the moon-earth and sun-earth axes approximately coincide every 15 days (syzygy). This causes a 15-day cycle of neap tide and spring tide; spring tide follows full moon and new moon and neap tide follows half-moon (with a delay of one or two days due to frictional dissipation <ref> Garrett, C.J.R. and Munk, W.H. 1971. The age of the tide and the "Q" of the oceans. Deep-Sea Res. 18: 493-503</ref>). In fact, the 15-day period corresponds to the frequency difference of the semidiurnal lunar component (<math>M_2</math>) and the semidiurnal solar component (<math>S_2</math>); the interference of these components produces the neap-spring variation of the tidal amplitude.
+
Due to the <math>\approx</math> 30-day orbital motion of the moon, the moon-earth and sun-earth axes approximately coincide every 15 days (syzygy). This causes a 15-day cycle of neap tide and spring tide; spring tide follows full moon and new moon and neap tide follows half-moon (with a delay of one or two days due to frictional dissipation <ref> Garrett, C.J.R. and Munk, W.H. 1971. The age of the tide and the "Q" of the oceans. Deep-Sea Res. 18: 493-503</ref>). In fact, the 15-day period corresponds to the frequency difference of the semidiurnal lunar component (<math>M_2</math>) and the semidiurnal solar component (<math>S_2</math>); the interference of these components produces the neap-spring variation of the tidal amplitude.
  
 
===Other tidal components===
 
===Other tidal components===
  
−
[[Image:WorldDomM2.png|thumb|right|400px|Fig.2. Coastal zones with dominant semi-diurnal tide.]]
+
[[Image:WorldDomM2.png|thumb|right|400px|Fig. 3. Coastal zones with dominant semi-diurnal tide.]]
  
−
The different cycles in the relative motions of moon, sun and earth surface generate tidal waves with corresponding periods. The lunar semidiurnal tidal component (<math>M_2</math>, period <math>\approx</math> 12 h 25 min) is generally the largest tidal constituent (see Fig.2), followed by the semidiurnal solar tide <math>S_2</math>.
+
The different cycles in the relative motions of moon, sun and earth surface generate tidal waves with corresponding periods. The lunar semidiurnal tidal component (<math>M_2</math>, period <math>\approx</math> 12 h 25 min) is generally the largest tidal constituent (see Fig. 3), followed by the semidiurnal solar tide <math>S_2</math> (period = 12 h).
 
Other important tidal constituents are:  
 
Other important tidal constituents are:  
 
* the diurnal component <math>K_1</math>, which is related to the declination of the lunar and solar orbits relative to the equatorial plane (period <math>\approx</math> 24 h),  
 
* the diurnal component <math>K_1</math>, which is related to the declination of the lunar and solar orbits relative to the equatorial plane (period <math>\approx</math> 24 h),  
Line 55: Line 60:
  
 
===Asymmetric ocean tides===
 
===Asymmetric ocean tides===
−
Because of the minor role of friction in the propagation of ocean tides, individual astronomic tidal components are well described by sinusoidal functions. This implies that for each component the rising and falling branches are symmetric. This also holds on average for a superposition of tidal components, if the frequencies <math>\omega_i</math> of the major tidal components are not linearly related with integer coefficients (<math>\omega_i</math> is different from any combination of sums and differences of <math>\omega_j, \; j \neq i</math>). Taken over a sufficiently long time interval the average period of rising tide then equals the average period of falling tide. Hence, at the continental shelf boundary there is symmetry between the astronomical forcing of flood currents and ebb currents.  
+
Because of the minor role of friction in the propagation of ocean tides, individual astronomic tidal components are well described by sinusoidal functions. This implies that for each component the rising and falling branches are symmetric. This also holds on average for a superposition of tidal components, if the frequencies <math>\omega_i</math> of the major tidal components are not linearly related with integer coefficients (<math>\omega_i</math> is different from any combination of sums and differences of <math>\omega_j, \; j \neq i</math>). Taken over a sufficiently long time the average period of rising tide then equals the average period of falling tide. Hence, at the continental shelf boundary there is symmetry between the astronomical forcing of flood currents and ebb currents.  
  
−
However, certain combinations of astronomic components yield asymmetric tides, irrespective of the averaging period. The reason is that most tidal constituents result from a superposition of a limited number of basic cycles in the relative motions of earth, moon and sun. The frequencies of these tidal constituents correspond to sums and differences of the basic frequencies <ref> Doodson, A.T. 1921. The harmonic development of the tide-generating potential. Proc. R. Soc. London, Ser.A 100: 305-329</ref>. This implies that different tidal constituents may interfere in such a way that flood and ebb are modulated in a systematic, asymmetric way. Such asymmetries may become significant in the case of strong diurnal tides; for dominant semidiurnal tides this effect is small <ref> Hoitink, A.F.J., Hoekstra, P. and van Mare, D.S. 2003. Flow asymmetry associated with astronomical tides: Implications for residual transport of sediment. J.Geophys.Res. 108: 13-1 - 13-8</ref>. A world map of tidal asymmetry based on harmonic analysis of 335 tidal stations worldwide has been established by Song et al. (2011)<ref>Song, D., X. H. Wang, A. E. Kiss, and Bao, X. 2011. The contribution to tidal asymmetry by different combinations of tidal constituents. J. Geophys. Res., 116, C12007</ref>.
+
[[Image:TidalAsymmetryWorldMap.jpg|thumb|right|500px|Fig. 4. World map of tidal asymmetry. The colors represent a measure of the difference in duration between falling tide and rising tide. A positive value close to 1 (red) represents a much steeper tidal rise than tidal fall and a large negative value close to -1 (blue) represents a much steeper tidal fall than tidal rise. The precise definition of the tidal asymmetry indicator is given in the original publication by Song et al. (2011)<ref name=S>Song, D., X. H. Wang, A. E. Kiss, and Bao, X. 2011. The contribution to tidal asymmetry by different combinations of tidal constituents. J. Geophys. Res., 116, C12007</ref>.]]
  
−
A particular example is the combination of the <math>M_2, K_1</math> and <math>O_1</math> tides. The sum of the frequencies of the <math>K_1</math> and <math>O_1</math> tidal constituents equals the frequency of the <math>M_2</math> tidal constituent. In regions where the amplitudes of the <math>K_1</math> and <math>O_1</math> tides are not small compared to the amplitude of the <math>M_2</math> tide, the sum of these three tidal constituents yields an asymmetric tide, with an asymmetry depending on the respective phases of these tidal constituents. Along the Californian coast, for example, the combination of <math>M_2, K_1</math> and <math>O_1</math> yields a tidal asymmetry with longer duration of rising tide compared to falling tide <ref> Nidzieko, J. 2010. Tidal asymmetry in estuaries with mixed semidiurnal/diurnal tides. J. Geophysical Research 115, C08006, doi:10.1029/2009JC005864</ref>. Duration asymmetry of tidal rise and tidal fall induces an asymmetry in the strength of flood and ebb currents in tidal inlets. This has consequences for residual sediment transport and for the morphology of the inward tidal basins (see [[Morphology of estuaries]] for more details).  
+
However, certain combinations of astronomic components yield asymmetric tides, irrespective of the averaging period. The reason is that most tidal constituents result from a superposition of a limited number of basic cycles in the relative motions of earth, moon and sun. The frequencies of these tidal constituents correspond to sums and differences of the basic frequencies <ref> Doodson, A.T. 1921. The harmonic development of the tide-generating potential. Proc. R. Soc. London, Ser.A 100: 305-329</ref>. This implies that different tidal constituents may interfere in such a way that flood and ebb are modulated in a systematic, asymmetric way. Such asymmetries may become significant in the case of strong diurnal tides <ref>Hoitink, A.F.J., Hoekstra, P. and van Mare, D.S. 2003. Flow asymmetry associated with astronomical tides: Implications for residual transport of sediment. J.Geophys.Res. 108: 13-1 - 13-8</ref>; for dominant semidiurnal tides this effect is small. Fig. 4 shows a world map of tidal asymmetry  computed according to the tidal constants derived from TPXO7-ATLAS by Song et al. (2011)<ref name=S></ref>.
 +
 
 +
A particular example is the combination of the <math>M_2, K_1</math> and <math>O_1</math> tides. The sum of the frequencies of the <math>K_1</math> and <math>O_1</math> tidal constituents equals the frequency of the <math>M_2</math> tidal constituent. In regions where the amplitudes of the <math>K_1</math> and <math>O_1</math> tides are not small compared to the amplitude of the <math>M_2</math> tide, the sum of these three tidal constituents yields an asymmetric tide, with an asymmetry depending on the relative phase of these tidal constituents. Along the Californian coast, for example, the combination of <math>M_2, K_1</math> and <math>O_1</math> yields a tidal asymmetry with longer duration of rising tide compared to falling tide <ref> Nidzieko, J. 2010. Tidal asymmetry in estuaries with mixed semidiurnal/diurnal tides. J. Geophysical Research 115, C08006, doi:10.1029/2009JC005864</ref>. Duration asymmetry of tidal rise and tidal fall induces an asymmetry in the strength of flood and ebb currents in tidal inlets. This has consequences for residual sediment transport and for the morphology of the inward tidal basins (see [[Tidal asymmetry and tidal basin morphodynamics]] and [[Morphology of estuaries]] for more details).  
  
  
Line 67: Line 74:
 
The tides generated in the ocean propagate to the continental shelf, where the tidal range may increase further. Different phenomena contribute to this amplification: resonant dimensions of the shelf sea, slowing down of wave-energy propagation ('shoaling') or concentration of the tidal energy flux in areas of reduced width ('funneling'). The maximum spring tidal range can exceed 14 m in some funnel-shaped bays, such as the Bay of Fundy (Canada), Bristol Channel (UK) and Baie du Mont Saint Michel (France).  
 
The tides generated in the ocean propagate to the continental shelf, where the tidal range may increase further. Different phenomena contribute to this amplification: resonant dimensions of the shelf sea, slowing down of wave-energy propagation ('shoaling') or concentration of the tidal energy flux in areas of reduced width ('funneling'). The maximum spring tidal range can exceed 14 m in some funnel-shaped bays, such as the Bay of Fundy (Canada), Bristol Channel (UK) and Baie du Mont Saint Michel (France).  
  
−
Tidal amplification in shelf seas is counteracted by frictional momentum dissipation. The strong tidal motion occurring in many shelf seas is thus not locally produced by tide generating forces, but results from co-oscillation with ocean tides and from local topographic amplification. Numerical tidal studies for the northwest European shelf <ref> Pingree, R.D. and Griffiths, D.K. 1987. Tidal friction for semidiurnal tides. Cont.Shelf Res. 7: 1181-1209</ref> and for the East China shelf <ref> Kang, S.K., Lee, S.R. and Lie, H.J. 1998. Fine-grid tidal modelling of the Yellow and East China seas. Cont.Shelf Res. 18: 739-772</ref> show that the local tide generating force influences the co-oscillating semidiurnal tide in these shelf seas by no more than about 1%. This is the main reason why no substantial tidal motion is generated in shallow enclosed seas or lakes. Dissipation of ocean tidal energy is mainly due to frictional dissipation in shelf seas <ref>Munk, W. 1997. Once again: once again - tidal friction. Prog. Oceanog. 40: 7-35</ref>; however, non-negligible dissipation also takes place in the ocean <ref>Egbert, G.D. and Ray, R.D. 2000. Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data. Nature 405: 775-778</ref>. Tidal resonance in shelf seas generally has a damping effect on ocean tides <ref> Arbic, B.K., Karsten, R.H. and Garrett, C. 2009. On tidal resonance in the global ocean and the back‐effect of coastal tides upon open‐ocean tides. Atmosphere-Ocean, 47: 239-266</ref>.
+
Tidal amplification in shelf seas is counteracted by frictional momentum dissipation. The strong tidal motion occurring in many shelf seas is thus not locally produced by tide generating forces, but results from co-oscillation with ocean tides and from local topographic amplification. Numerical tidal studies for the northwest European shelf <ref> Pingree, R.D. and Griffiths, D.K. 1987. Tidal friction for semidiurnal tides. Cont.Shelf Res. 7: 1181-1209</ref> and for the East China shelf <ref> Kang, S.K., Lee, S.R. and Lie, H.J. 1998. Fine-grid tidal modelling of the Yellow and East China seas. Cont.Shelf Res. 18: 739-772</ref> show that the local tide generating force influences the co-oscillating semidiurnal tide in these shelf seas by no more than about 1%. Tidal resonance in shelf seas generally has a damping effect on ocean tides <ref> Arbic, B.K., Karsten, R.H. and Garrett, C. 2009. On tidal resonance in the global ocean and the back‐effect of coastal tides upon open‐ocean tides. Atmosphere-Ocean, 47: 239-266</ref>.
  
 
===Higher harmonic components===
 
===Higher harmonic components===
  
−
[[Image:worldmapM4.png|thumb|right|400px|Fig.3. Coastal zones with important quarter-diurnal tide.]]
+
[[Image:worldmapM4.png|thumb|right|400px|Fig. 5. Coastal zones with important quarter-diurnal tide.]]
−
 
 
−
Tides on the continental shelf are due to co-oscillation with the ocean tides at the continental shelf boundaries, as noted earlier. However, the non-linearity of tidal propagation in shallow environments with strong topography (presence of large tidal flats, for example) alters the sinusoidal character of the ocean tide at the shelf boundary. The distortion of the tidal wave can be represented by additional tidal components corresponding to multiples of the dominant ocean tidal frequencies <ref> Aubrey, D.G. and Speer, P.E. 1985. A study of non-linear tidal propagation in shallow inlet/estuarine systems. Part I: Observations. Est. Coast. Shelf Sci. 21: 185-205</ref><ref> Friedrichs, C. T., and Aubrey, D. G. 1988. Non-linear tidal distortion in shallow well-mixed estuaries: a synthesis. Estuarine, Coastal and Shelf Science, 27: 521-545</ref><ref>Boy, J.-P., Llubes, M., Ray, R., Hinderer, J., Florsch, N., Rosat, S., Lyard, F. and Letellier, T. 2004. Non-linear oceanic tides observed by superconducting gravimeters in Europe. J. Geodynamics 38: 391–405</ref>. An important consequence of tidal wave distortion is the asymmetric character of tidal motion in shallow water: the periods of tidal rise and tidal fall are not equal. This asymmetry is represented in particular by a quarter-diurnal tidal component (indicated by M4), which induces different strengths of flood currents and ebb currents. In Fig. 3 coastal regions are indicated with an important M4 tidal component; they coincide largely with coastal zones where the semidiurnal tide is strong (Fig. 2). Tidal asymmetry in shallow coastal waters, estuaries and tidal rivers, plays a crucial role in tide-topography interaction <ref name=D></ref>, because of the highly non-linear dependence of sediment transport on tidal current strength. A further explanation is given below.
 
−
 
 
−
===Ebb-flood asymmetry and coastal basin morphodynamics===
 
  
−
[[Image:TidalBorePetitcodiacRiver.jpg|thumb|right|400px|Fig.4. Tidal bore in the Petitcodiac River (Bay of Fundy, Canada).]]
+
Tides on the continental shelf are due to co-oscillation with the ocean tides at the continental shelf boundaries, as noted earlier. However, the non-linearity of tidal propagation in shallow environments (water depth no much greater than ten times the tidal amplitude, or less) alters the sinusoidal character of the ocean tide at the shelf boundary. The distortion of the tidal wave can be represented by additional tidal components corresponding to multiples (overtides) or superposition (compound tides) of the dominant ocean tidal frequencies <ref> Aubrey, D.G. and Speer, P.E. 1985. A study of non-linear tidal propagation in shallow inlet/estuarine systems. Part I: Observations. Est. Coast. Shelf Sci. 21: 185-205</ref><ref> Friedrichs, C. T., and Aubrey, D. G. 1988. Non-linear tidal distortion in shallow well-mixed estuaries: a synthesis. Estuarine, Coastal and Shelf Science, 27: 521-545</ref><ref>Boy, J.-P., Llubes, M., Ray, R., Hinderer, J., Florsch, N., Rosat, S., Lyard, F. and Letellier, T. 2004. Non-linear oceanic tides observed by superconducting gravimeters in Europe. J. Geodynamics 38: 391–405</ref>. An important consequence of tidal wave distortion is the asymmetric character of tidal motion in shallow water: the periods of tidal rise and tidal fall are not equal. This asymmetry is represented in particular by a quarter-diurnal tidal component (indicated by M4), which induces different strengths of flood currents and ebb currents. In Fig. 5, coastal regions are indicated with an important M4 tidal component; they coincide largely with coastal zones where the semidiurnal tide is strong (Fig. 3).  
  
−
In bays and estuaries where the tidal amplitude is comparable to or larger than the average water depth the high-water crest of the tidal wave travels much faster than the low-water trough. In this case the tidal wave distortion can become so strong that the high-water crest overtakes the low-water trough. The tidal flood wave then propagates inland as a bore (see Fig. 4). Tidal bores are common in funnel-shaped shallow bays and estuaries with strongly amplified tides (for example the funnel-shaped bays mentioned above), especially for spring tidal conditions <ref>Bonneton, P., Bonneton, N., Parisot, J.-P. and Castelle B. 2015. Tidal bore dynamics in funnel-shaped estuaries, J. Geophys. Res. Oceans 120: 923–941, doi:10.1002/2014JC010267.</ref>. The flood current during the passage of the bore is very strong and largely exceeds the maximum currents occurring during ebb. The most famous tidal bore occurs in the Qiantang estuary (China) <ref>Jiyu, C., Cangzi, L., Chongle, Z. and Walker, H.J. 1990. Geomorphological development and sedimentation in Qiantang estuary and Hangzou Bay. J.Coast.Res. 6: 559-572</ref>. See also the article [[Tidal wave deformation and tidal bores]].
 
  
−
More in general, one may distinguish two causes of tidal wave asymmetry <ref> Dronkers, J. 1986. Tidal asymmetry and estuarine morphology. Neth.J.Sea Res. 20: 117-131</ref>.
+
==Tides in estuaries and tidal lagoons==
  
−
# Water depths in the tidal basin are substantially larger at high water than at low water and there is less frictional dissipation during the passage of the high-water wave crest than during the passage of the low-water trough. The tidal wave crest then propagates faster into the basin than the tidal wave trough and the period of tidal rise (from low water to high water) will thus be shorter than the period of tidal fall (from high water to low water). This implies that flood currents will be on average stronger than ebb currents.
+
The tidal wave is further distorted when entering coastal inlets and estuaries. This is due the shallowness of these systems (the water depth is in many cases no greater than a few times the tidal amplitude or even less) and due to interaction with the basin topography (for example, expansion of the tidal flood wave over intertidal flats). As a consequence of tidal asymmetry, substantial differences may arise between the strength of flood and ebb currents. This results in a net import or export of sediment and corresponding sedimentation or erosion. The basin morphology will evolve and tidal asymmetry will change consequently. This morphodynamic feedback process is described in more detail in the article [[Tidal asymmetry and tidal basin morphodynamics]]. Tidal distortion in some estuaries and shallow tidal lagoons may become so strong that the tidal flood wave evolves into a tidal bore. This process is described in more detail in the article [[Testpage3|Tidal bore dynamics]].  
−
#The main tidal channel of the tidal basin is bordered by large intertidal flats. The propagation of the tidal wave crest is retarded, because of lateral expansion of the tidal flood wave over the intertidal flats. The high-water wave crest then propagates into the basin more slowly than the low-water wave trough, which travels through the main tidal channel. In this case the period of tidal rise will be longer than the period of tidal fall and consequently ebb currents will be on average stronger than flood currents.  
 
  
−
In most shallow tidal bays and estuaries both processes compete. This competition may lead to approximately equal strength of flood and ebb currents, in spite of strong nonlinearity of tidal wave propagation in these systems. When flood and ebb currents have approximately equal strength the tidally averaged residual sediment transport along the tidal basin will be small and the basin bathymetry will be in a state close to morphodynamic equilibrium. When flood sediment transport and ebb sediment transport are not in balance the tidal basin morphology will evolve (changing channel depth and intertidal area), until reaching a state of morphodynamic equilibrium <ref>Dronkers, J. 1998. Morphodynamics of the Dutch Delta. In: Physics of estuaries and coastal seas. Ed.: J.Dronkers and M.B.A.M. Scheffers, Balkema, Rotterdam: 297-304</ref>.
 
  
 
    
 
    
Line 92: Line 92:
 
:[[Tidal motion in shelf seas]]
 
:[[Tidal motion in shelf seas]]
 
:[[Coriolis acceleration]]
 
:[[Coriolis acceleration]]
−
:[[Tidal wave deformation and tidal bores]]
+
:[[Tidal asymmetry and tidal basin morphodynamics]]
 
:[[Morphology of estuaries]]
 
:[[Morphology of estuaries]]
 +
:[[Tidal bore dynamics]]
  
  
Line 109: Line 110:
  
  
−
{{author
+
{{2Authors
−
|AuthorID=120
+
|AuthorID1=120
−
|AuthorFullName=Job Dronkers
+
|AuthorFullName1=Job Dronkers
−
|AuthorName=Dronkers J}}
+
|AuthorName1=Dronkers J
 +
|AuthorID2=99999
 +
|AuthorFullName2=Dehai Song
 +
|AuthorName2=Song D
 +
}}
  
 
[[Category:Land and ocean interactions]]
 
[[Category:Land and ocean interactions]]

Revision as of 14:21, 13 June 2019

In this article the term tide refers to the astronomical tide.


Introduction

Tidal motion is the oscillation of ocean waters under the influence of the attractive gravitational forces of the moon and the sun. The response of the ocean to the gravitational forces follows a pattern of rotating ('amphidromic') systems, as a consequence of earth's rotation. The frequencies are determined by the relative periodic motions of moon, sun and earth surface. The amplitude of the tidal oscillation is very small compared to ocean depths. The ocean tidal oscillation in each point can therefore be represented by a linear superposition of sinusoidal tidal components with frequencies corresponding to the different cycles of the gravitational forces. The most important tidal components have a periodicity which is close to semidiurnal or diurnal, due to earth's rotation.


Tide generation

Moon and sun

The regular daily upward and downward motion of the water surface along the coastline is the most visible expression of tidal forcing. In ancient Greece it was recognized that tides are in some way related to sun and moon, but this relationship could not be explained [1]. The explanation of tidal motion as resulting from gravitational forces was given by Newton. The lunar and solar tide generating forces acting on the oceans are extremely small; they are about a factor [math]\, 10^{-7} \,[/math] smaller than the gravitational force of the earth. The tide-generating force of the moon is about twice as large as that of the sun.

Tidal wave and ocean basin resonance

Ocean tides owe their strength for a large part to resonance; tidal motion is amplified for tidal components with a frequency close to the frequency of free oscillations in the ocean basins. This is the case in particular for the semi-diurnal tide in the North Atlantic and Pacific Oceans [2], and also for the diurnal tide in the Pacific Ocean [3]. Tidal waves in wide ocean basins (width typically larger than a few thousand km) rotate around points of zero amplitude, the amphidromic points; the rotation is counterclockwise in the Northern Hemisphere and clockwise in the Southern Hemisphere. This due to earth's rotation, which induces Coriolis acceleration of tidal currents. Fig.1 shows the semi-diurnal tidal wave in the world's oceans; it comprises a large number of amphidromic systems, where the tide rotates in resonance with the semi-diurnal component of the gravitational force. This ocean tidal wave pattern can be described in first approximation by a combination of Kelvin and Sverdrup waves (also called Poincaré waves, see Tidal motion in shelf seas).


Fig. 1. System of semidiurnal lunar tidal waves ([math]M_2[/math]) in the oceans represented by lines of equal tidal phase (solid, intervals of 30[math]^{\circ}[/math]) and lines of equal tidal amplitude (dashed, intervals of 0.25 m). Three ranges are indicated for the tidal amplitude [math]a[/math] on the continental shelf: microtidal (white fringe, [math]a \lt [/math] 1 m), mesotidal (light grey fringe, 1 [math] \lt a \lt [/math] 2 m) and macrotidal (dark grey fringe, [math]a \gt [/math] 2 m). Redrawn after Bearman (1991) [4]

Tidal Energy Dissipation

The total power available from Moon and Sun on the global ocean is estimated at 3.7 TW ([math]10^{12}[/math] Watts); after allowing for a comparatively small dissipation in the atmosphere and the solid Earth, 3.5 TW remain to be dissipated in the ocean (Munk and Wunsch, 1998)[5]. For comparison, the geothermal heat loss is 30 TW, and the equator-to-pole ocean heat-flow is 2,000 TW. Solar radiation input (175,000 TW) is five orders of magnitude greater than the tidal power.

Fig. 2. Estimates of [math]M_2[/math] tidal energy dissipation based on six years of altimeter data from the TOPEX/Poseidon satellite. The blue patches (negative dissipation) are clearly not physical, and provide some indication of the magnitude of noise in the estimates (Egbert and Ray, 2000)[6]. Image from NASA.

The tidal energy dissipation due to the [math]M_2[/math] tide can be exactly calculated from astronomic observation programs at 2.5 TW, of which 0.1 TW is dissipated in the atmosphere and the solid Earth (Munk, 1997)[7]. It is estimated that 1.8 TW of [math]M_2[/math] energy (2.5 TW of all lunar and solar constituents) is lost in the turbulent bottom boundary layers of marginal seas due to the work against bottom friction which opposes tidal currents. This kind of energy dissipation is concentrated in a few shelf areas of strong tidal current, such as the north-west European Shelf, the Patagonian Shelf, the Yellow Sea, the Timor and Arafura Seas, and the Amazon Shelf (Fig. 2). The other 0.6 TW of [math]M_2[/math] tidal dissipation (1.0 TW of all lunar and solar constituents) occurs in the open ocean through the scattering by ocean-bottom topography of surface tides into internal tidal waves (Egbert and Ray, 2000). The breaking of internal waves may be concentrated in a few areas, generally near rugged bottom topography, for example seamounts and mid-ocean ridges (Fig. 2), and is believed to be a principal contributor to drive the ocean interior mixing (Munk and Wunsch, 1998)[5].

Modelling ocean tides

Modelling ocean tides remains a challenge, even with modern fast computers. Because the tidal wavelength is much larger than ocean depth, these models are generally based on the hydrostatic shallow-water equations. Relatively simple models considering the response of a homogeneous ocean to the tide-generating forces yield results in qualitative agreement with observations. However, for better quantitative agreement stratification and internal tide generation (at ocean ridges, in particular) should be included. Other factors that need to be taken into account are:

  • Tide-induced seafloor deformation under the weight of the water column (loading tide);
  • Tide-induced seafloor deformation related to the solid earth tide;
  • Gravitational attraction induced by the mass of the ocean on the ocean itself (self-attraction).

See Hendershott (2007) [8] for a discussion of these different factors.


Tidal components

Semidiurnal periodicity

In order to explain tidal motion, it is not sufficient to consider only the gravitational forces exerted by moon and sun on the earth's water masses. Tide generation results from the local imbalance at the earth's surface of two opposing factors: the gravitational forces acting between the earth and the moon (and between the earth and the sun), and the centrifugal acceleration related to the orbital motions of these celestial bodies. In fact, only the tangential component of the gravitational force is relevant - water is not accelerated away from the earth's surface. Because the gravitational force and the centrifugal acceleration are in balance at any location on the earth's surface twice during each diurnal rotation, the major periodicity is approximately semidiurnal (a little more than 12 hours because of moon's orbital motion).

Diurnal tide and spring-neap cycle

Because the solar and lunar orbits do not coincide with the equatorial plane (the angle between orbital plane and equatorial plane is called declination), a daily inequality arises in the semidiurnal cycle. The daily inequality is strongest in shelf seas that resonate at diurnal frequency and which are situated close to amphodromic points of the semidiurnal tide. In such regions the tide is mainly diurnal.

Due to the [math]\approx[/math] 30-day orbital motion of the moon, the moon-earth and sun-earth axes approximately coincide every 15 days (syzygy). This causes a 15-day cycle of neap tide and spring tide; spring tide follows full moon and new moon and neap tide follows half-moon (with a delay of one or two days due to frictional dissipation [9]). In fact, the 15-day period corresponds to the frequency difference of the semidiurnal lunar component ([math]M_2[/math]) and the semidiurnal solar component ([math]S_2[/math]); the interference of these components produces the neap-spring variation of the tidal amplitude.

Other tidal components

Fig. 3. Coastal zones with dominant semi-diurnal tide.

The different cycles in the relative motions of moon, sun and earth surface generate tidal waves with corresponding periods. The lunar semidiurnal tidal component ([math]M_2[/math], period [math]\approx[/math] 12 h 25 min) is generally the largest tidal constituent (see Fig. 3), followed by the semidiurnal solar tide [math]S_2[/math] (period = 12 h). Other important tidal constituents are:

  • the diurnal component [math]K_1[/math], which is related to the declination of the lunar and solar orbits relative to the equatorial plane (period [math]\approx[/math] 24 h),
  • the diurnal lunar component [math]O_1[/math] (period [math]\approx[/math] 26 h) and
  • the diurnal solar component [math]P_1[/math] (period [math]\approx[/math] 24 h).

There are many other tidal components of smaller magnitude and lower frequency related to periodicity in the lunar and terrestrial orbits. A modulation of the mean tidal amplitude of the order of 5% is related to the 18.6 year oscillation in the declination of the lunar orbit.

Prediction of tides

Because the astronomical tide responds to a cyclic forcing by the gravitational motions of earth, moon and sun (including earth's rotation), tides are a cyclic phenomenon at any place on earth and can be predicted by analysing observations from the past. Therefore the amplitude and phase of all relevant tidal components need to be determined. The most usual method today is based on the least-squares technique [10]. The tidal elevation is represented by a sum of the (sinusoidal) tidal components that are expected to yield a significant contribution. The amplitudes and phases of the tidal components are free parameters which are determined by a least-square fit of the representation to the observed tidal elevation record. The tidal record should be sufficiently long to eliminate meteorological influences. The observation record should also be longer (at least a few times) than the largest period appearing in the representation. For resolving two components with close periods [math]T[/math] and [math]T+\Delta T[/math] the length of the observation record should exceed a few times [math]\; T^2 / \Delta T [/math]. For many stations around the world tidal predictions are available (see for example https://maree.shom.fr/) .

Asymmetric ocean tides

Because of the minor role of friction in the propagation of ocean tides, individual astronomic tidal components are well described by sinusoidal functions. This implies that for each component the rising and falling branches are symmetric. This also holds on average for a superposition of tidal components, if the frequencies [math]\omega_i[/math] of the major tidal components are not linearly related with integer coefficients ([math]\omega_i[/math] is different from any combination of sums and differences of [math]\omega_j, \; j \neq i[/math]). Taken over a sufficiently long time the average period of rising tide then equals the average period of falling tide. Hence, at the continental shelf boundary there is symmetry between the astronomical forcing of flood currents and ebb currents.

Fig. 4. World map of tidal asymmetry. The colors represent a measure of the difference in duration between falling tide and rising tide. A positive value close to 1 (red) represents a much steeper tidal rise than tidal fall and a large negative value close to -1 (blue) represents a much steeper tidal fall than tidal rise. The precise definition of the tidal asymmetry indicator is given in the original publication by Song et al. (2011)[11].

However, certain combinations of astronomic components yield asymmetric tides, irrespective of the averaging period. The reason is that most tidal constituents result from a superposition of a limited number of basic cycles in the relative motions of earth, moon and sun. The frequencies of these tidal constituents correspond to sums and differences of the basic frequencies [12]. This implies that different tidal constituents may interfere in such a way that flood and ebb are modulated in a systematic, asymmetric way. Such asymmetries may become significant in the case of strong diurnal tides [13]; for dominant semidiurnal tides this effect is small. Fig. 4 shows a world map of tidal asymmetry computed according to the tidal constants derived from TPXO7-ATLAS by Song et al. (2011)[11].

A particular example is the combination of the [math]M_2, K_1[/math] and [math]O_1[/math] tides. The sum of the frequencies of the [math]K_1[/math] and [math]O_1[/math] tidal constituents equals the frequency of the [math]M_2[/math] tidal constituent. In regions where the amplitudes of the [math]K_1[/math] and [math]O_1[/math] tides are not small compared to the amplitude of the [math]M_2[/math] tide, the sum of these three tidal constituents yields an asymmetric tide, with an asymmetry depending on the relative phase of these tidal constituents. Along the Californian coast, for example, the combination of [math]M_2, K_1[/math] and [math]O_1[/math] yields a tidal asymmetry with longer duration of rising tide compared to falling tide [14]. Duration asymmetry of tidal rise and tidal fall induces an asymmetry in the strength of flood and ebb currents in tidal inlets. This has consequences for residual sediment transport and for the morphology of the inward tidal basins (see Tidal asymmetry and tidal basin morphodynamics and Morphology of estuaries for more details).


Tides on the continental shelf and in coastal basins

Tidal amplification

The tides generated in the ocean propagate to the continental shelf, where the tidal range may increase further. Different phenomena contribute to this amplification: resonant dimensions of the shelf sea, slowing down of wave-energy propagation ('shoaling') or concentration of the tidal energy flux in areas of reduced width ('funneling'). The maximum spring tidal range can exceed 14 m in some funnel-shaped bays, such as the Bay of Fundy (Canada), Bristol Channel (UK) and Baie du Mont Saint Michel (France).

Tidal amplification in shelf seas is counteracted by frictional momentum dissipation. The strong tidal motion occurring in many shelf seas is thus not locally produced by tide generating forces, but results from co-oscillation with ocean tides and from local topographic amplification. Numerical tidal studies for the northwest European shelf [15] and for the East China shelf [16] show that the local tide generating force influences the co-oscillating semidiurnal tide in these shelf seas by no more than about 1%. Tidal resonance in shelf seas generally has a damping effect on ocean tides [17].

Higher harmonic components

Fig. 5. Coastal zones with important quarter-diurnal tide.

Tides on the continental shelf are due to co-oscillation with the ocean tides at the continental shelf boundaries, as noted earlier. However, the non-linearity of tidal propagation in shallow environments (water depth no much greater than ten times the tidal amplitude, or less) alters the sinusoidal character of the ocean tide at the shelf boundary. The distortion of the tidal wave can be represented by additional tidal components corresponding to multiples (overtides) or superposition (compound tides) of the dominant ocean tidal frequencies [18][19][20]. An important consequence of tidal wave distortion is the asymmetric character of tidal motion in shallow water: the periods of tidal rise and tidal fall are not equal. This asymmetry is represented in particular by a quarter-diurnal tidal component (indicated by M4), which induces different strengths of flood currents and ebb currents. In Fig. 5, coastal regions are indicated with an important M4 tidal component; they coincide largely with coastal zones where the semidiurnal tide is strong (Fig. 3).


Tides in estuaries and tidal lagoons

The tidal wave is further distorted when entering coastal inlets and estuaries. This is due the shallowness of these systems (the water depth is in many cases no greater than a few times the tidal amplitude or even less) and due to interaction with the basin topography (for example, expansion of the tidal flood wave over intertidal flats). As a consequence of tidal asymmetry, substantial differences may arise between the strength of flood and ebb currents. This results in a net import or export of sediment and corresponding sedimentation or erosion. The basin morphology will evolve and tidal asymmetry will change consequently. This morphodynamic feedback process is described in more detail in the article Tidal asymmetry and tidal basin morphodynamics. Tidal distortion in some estuaries and shallow tidal lagoons may become so strong that the tidal flood wave evolves into a tidal bore. This process is described in more detail in the article Tidal bore dynamics.


Related articles

Tidal motion in shelf seas
Coriolis acceleration
Tidal asymmetry and tidal basin morphodynamics
Morphology of estuaries
Tidal bore dynamics


Further reading

Cartwright, D.E. 1999. Tides, a scientific history. Cambridge Univ.Press, UK, 292 pp.

Pedlosky, J. 1979. Geophysical Fluid Dynamics. Springer Verlag, 624 pp.


References

  1. ↑ Ekman, M. 1993. A concise history of the theories of tides, precession-nutation and polar motion. Surveys in Geophysics 14: 585-617
  2. ↑ Heath, R.A. 1981. Estimates of the resonant period and Q in the semi-diurnal tidal band in the North Atlantic and Pacific Oceans. Deep-Sea Research. Vol. 28A: 481 – 493
  3. ↑ Müller, M. 2007. The free oscillations of the world ocean in the period range 8 to 165 hours including the full loading effect. Geophys. Res. Letters 34, L05606, doi:10.1029/2006GL028870, 2007
  4. ↑ Bearman, G. (Ed.) 1991. Waves, tides and shallow-water processes. The Open University, Pergamon Press, Oxford
  5. ↑ 5.0 5.1 Munk, W. H. and Wunsch C. 1998. Abyssal recipes II: Energetics of tidal and wind mixing, Deep-Sea Research 45: 1977-2010
  6. ↑ Egbert, G. D., and R. D. Ray (2000), Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data, Nature, 405, 775-778
  7. ↑ Munk, W. H. 1997. Once again: once again–tidal friction, Progress in Oceanography 40: 7-35
  8. ↑ Hendershott, M.C. 2007. Long Waves and Ocean Tides. In: Evolution of Physical Oceanography (Eds. B. Warren, and C. Wunsch) MIT OpenCourseWare, https://ocw.mit.edu
  9. ↑ Garrett, C.J.R. and Munk, W.H. 1971. The age of the tide and the "Q" of the oceans. Deep-Sea Res. 18: 493-503
  10. ↑ Parker, B.B. 2007. Tidal Analysis and Prediction. NOAA Special Publication NOS CO-OPS 3
  11. ↑ 11.0 11.1 Song, D., X. H. Wang, A. E. Kiss, and Bao, X. 2011. The contribution to tidal asymmetry by different combinations of tidal constituents. J. Geophys. Res., 116, C12007
  12. ↑ Doodson, A.T. 1921. The harmonic development of the tide-generating potential. Proc. R. Soc. London, Ser.A 100: 305-329
  13. ↑ Hoitink, A.F.J., Hoekstra, P. and van Mare, D.S. 2003. Flow asymmetry associated with astronomical tides: Implications for residual transport of sediment. J.Geophys.Res. 108: 13-1 - 13-8
  14. ↑ Nidzieko, J. 2010. Tidal asymmetry in estuaries with mixed semidiurnal/diurnal tides. J. Geophysical Research 115, C08006, doi:10.1029/2009JC005864
  15. ↑ Pingree, R.D. and Griffiths, D.K. 1987. Tidal friction for semidiurnal tides. Cont.Shelf Res. 7: 1181-1209
  16. ↑ Kang, S.K., Lee, S.R. and Lie, H.J. 1998. Fine-grid tidal modelling of the Yellow and East China seas. Cont.Shelf Res. 18: 739-772
  17. ↑ Arbic, B.K., Karsten, R.H. and Garrett, C. 2009. On tidal resonance in the global ocean and the back‐effect of coastal tides upon open‐ocean tides. Atmosphere-Ocean, 47: 239-266
  18. ↑ Aubrey, D.G. and Speer, P.E. 1985. A study of non-linear tidal propagation in shallow inlet/estuarine systems. Part I: Observations. Est. Coast. Shelf Sci. 21: 185-205
  19. ↑ Friedrichs, C. T., and Aubrey, D. G. 1988. Non-linear tidal distortion in shallow well-mixed estuaries: a synthesis. Estuarine, Coastal and Shelf Science, 27: 521-545
  20. ↑ Boy, J.-P., Llubes, M., Ray, R., Hinderer, J., Florsch, N., Rosat, S., Lyard, F. and Letellier, T. 2004. Non-linear oceanic tides observed by superconducting gravimeters in Europe. J. Geodynamics 38: 391–405


The main authors of this article are Job Dronkers and Dehai Song
Please note that others may also have edited the contents of this article.
Citation: Job Dronkers; Dehai Song; (2019): Ocean and shelf tides. Available from http://www.coastalwiki.org/wiki/Ocean_and_shelf_tides [accessed on 22-11-2024]
Retrieved from "https://www.coastalwiki.org/w/index.php?title=Ocean_and_shelf_tides&oldid=74772"