Difference between revisions of "Rhythmic shoreline features"

From Coastal Wiki
Jump to: navigation, search
Line 165: Line 165:
  
 
[[Sediment transport formulas for the coastal environment]]
 
[[Sediment transport formulas for the coastal environment]]
 +
 +
[[Swash zone dynamics]]
 +
  
  

Revision as of 13:16, 2 June 2017

Introduction

Figure 1. Left: Rhythmic shoreline features forced by a breakwater system. Right: Picture taken at the Arcachon bay (courtesy of Isabel Casanovas) showing ripple marks and shoreline undulations ([math]L \sim [/math] 1-2 m) at low tide. On the right there is a wooden board. Existing studies demonstrate that the ripple marks are self-organized, emerging from an instability of the flat bed under the coupling of water and sand. The origin of the shoreline undulations is unknown but they are probably self-organized too, because there are no nearby features at these particular scales that could force them.

Sandy shorelines are rarely strait but they commonly exhibit undulations or cuspate shapes that are most often irregular. Sometimes, however, the shoreline position is nearly or roughly periodic in space along the shore with a wavelength [math]L[/math] or, at least, there exists the suggestion of a recurrent alongshore spacing [math]L[/math]. We then refer to these undulations or cuspate features as rhythmic shoreline features.

The spacing [math]L[/math] is sometimes dictated by external constraints like human-made structures (e.g., groins or breakwaters, see Figure 1a) or the inherited geology (e.g., sea bed large-scale morphology like drowned canyons). In other cases, a pre-existing hydrodynamic template can imprint its spacing [math]L[/math] on the developing morphology. This is the case of bars created by standing waves. We refer to these two types as forced features.

Intriguingly, rhythmic shoreline features can also exist without any forcing by external constraints or by a pre-existing template in the hydrodynamic forcing at the length scale [math]L[/math] (see Figure 1b). We refer to them as self-organized features [1]. We are here concerned with this class and we will hereinafter refer to them unless stated otherwise. They can be very striking, there are many types and their length scale [math]L[/math] can span several orders of magnitude, roughly from 1 m to 100 km (see Figure 2). It is hard to think that they simply come out of random processes and their simplicity or their ordered complexity strongly suggest that they are the result of collective processes at the length scale [math]L[/math] involving waves, currents, tides and sand. It has been found that they emerge out of positive feedbacks between the hydrodynamics and the morphology, and their spacing [math]L[/math] is internally generated as the length scale that makes the feedback most efficient.


Figure 2. Rhythmic shoreline features at various lengthscales. a) Beach cusps, [math]L\approx 2 [/math]m (Matingarahi, NZ. Source: courtesy of Prof. A.D. Short); b) up: megacups associated to transverse bars, [math]L \approx [/math]20 m (Ebro delta, Catalonia (Spain), image taken by the authors); b) down: large beach cusps [math]L \approx [/math] 60 m (Angola. Source: Google Earth, image from Digital-Globe); c) up: megacusps associated to a crescentic bar, [math]L \approx [/math] 300 m (Saint Cyprien, France. Source: Google Earth, image from Data SIO, NOAA, U.S. Navy, NGA, GEBCO); c) down: megacusps associated to transverse bars (Lighthouse Beach, NSW, Australia. Source: courtesy of Prof. A.D. Short), [math]L \approx [/math]500 m; d) up: rhythmic spits, [math]L \approx[/math] 7 km (Gulf of Amur. Source: Google Earth, image from TerraMetrics); d) down: shoreline sand waves, [math]L \approx[/math] 5 km (Namibia. Source: Google Earth, image from Digital Globe); e) rhythmic spits [math]L \approx[/math] 50-80 km (Azov sea. Source: Google Earth, image from Data SIO, NOAA, U.S. Navy, NGA, GEBCO).

Rhythmic shoreline features are interesting by themselves in the context of coastal geomorphology. But they are also a visible footprint of important physical mechanisms associated to the coupling between hydrodynamics and morphology so that their study offers a way of getting insight into this coupling. From an engineering point of view, the dynamics of shoreline undulations leads to the existence of erosional hotspots or zones of increased coastal vulnerability.

Rhythmic shoreline features can be classified either according to their alongshore lengthscale [math]L[/math] or according to the processes involved in their formation. According to the latter, we can distinguish three types: a) beach cusps, which are associated to swash zone processes, b) megacusps, which are associated to surf-zone processes and c) large scale shoreline features, which are associated to processes at a length scale which is larger than the surf zone width, [math]X_b[/math], so that [math]L \gg X_b[/math]. The length scale typically increases in the order a, b, c. However, depending mainly on the wave energy level, their lengthscale can overlap (see Figure 2). For instance, megacups or large scale shoreline features on low energy beaches can be smaller than cusps or megacusps on open ocean beaches, respectively. We will here deal with types b) and c), since beach cusps are specifically treated in another article (Beach Cusps by G.Coco).

Megacusps and rhythmic surf zone bars

Figure 3. Images from the Castelldefels beach video station (Catalonia, Spain) showing surf zone bar morphology at different times. a) shore parallel straight bar, b) incipient crescentic bar with relatively subtle undulations, c) large amplitude crescentic bar with crescents developped into transverse bars (TBR) attaching the shoreline and determining megacusps, d) complex morphology encompassing a crescentic bar, rip channels, megacups and small transverse medium-energy finger bars.

The surf zone of sandy beaches commonly features sand deposits or bars separated by bed depressions or troughs. The associated bathymetry is often complex and can be rhythmic in the alongshore direction. The rhythmic bar systems can influence the shoreline and imprint their wavelength [math]L[/math] on it. As shown in Figure 2c, the megacups are the resulting undulations or cuspate features on the shoreline. Bar systems can be very complex and sometimes it is difficult to assign any known type to the observed morphology (see Figure 3). But rhythmic bars are in principle classified into two types: crescentic bars and transverse bar systems.


Crescentic bars

A crescentic bar consists of an alongshore sequence of shallower and deeper sections alternating shoreward and seaward (respectively) of a line parallel to the shore in such a way that the bar shape is undulating in plan view ([2][3] [4] and references therein; also see Figures 2c and 3b, c, d ). In some cases the undulation is quite subtle, the bar being almost straight (Figure 3b), but occasionally, it features pronounced crescent moons with the horns pointing shoreward and the bays (deeps) located seaward (Figures 2c, 3c). The deeper sections are called rip channels because strong seaward directed currents called rip currents [5] [6] are concentrated there. This is why they are sometimes called rip channel systems. Note, however, that rip channels, i.e., cross-shore-oriented channels in the surf zone where rip currents concentrate, can also be observed associated to transverse bar systems without the presence of crescentic bars (see next section). Crescentic bars have been reported on microtidal to mesotidal sandy beaches at different scales with a mean alongshore spacing, [math]L[/math], ranging from tens of meters up to 2-3 km. They can influence the shoreline to form megacusps in two ways: directly, the horns of the crescentic bars connecting to the shoreline and thus forming the megacusps at the attachment points (Figure 3c) or indirectly, the bar and the shoreline being separated by a trough (Figure 3d). In the latter case the undulations in the crescentic bar and in the shoreline are still linked and roughly share the same alongshore spacing [math]L[/math]. This can happen because of the alongshore rhythmic topographic control exerted by the bars on the waves and by the induced circulation cells. Usually, the undulations are either in phase (i.e., seaward/shoreward displacements in phase) or out of phase (i.e., shoreward displacements of the bar in front of the seaward displacements of the shoreline and vice versa).

Transverse bar systems

Transverse bars extend perpendicularly to the coast or with an oblique orientation. No matter their angle with the shore normal being small or large. Shepard [7] introduced the term transverse bars to distinguish them from the shore-parallel bars. They usually occur in patches of a few of them up to tens, they are separated by troughs and they display a rhythmic pattern along the shore. Significant rip currents sometimes concentrate at the troughs that can then be considered rip channels [8]. The alongshore spacing, [math]L[/math], is defined as the distance between successive bar crests. They are typically attached to the shore and the shoreline attachments determine the megacusps. In the presence of an alongshore current, they migrate down-drift with migration rates up to [math]40[/math] m/d [9][10]. Oblique bars in this case can have its distal end shifted down-current or up-current with respect to the shore attachment and are then called down-current oriented or up-current oriented, respectively. They sometimes show an asymmetry of their cross-section (the down-current flank being steeper than the up-current flank [10]. Many types of transverse bars (in their characteristics and origin) have been reported in the literature and we here state a tentative classification based on that provided by [10]. However, we group two of the types in that paper in only one class because we think they do not essentially differ.


TBR Bars

They are associated to the Transverse Bar and Rip (TBR) state in the standard beach state classification [11] (see Figures 2c and 2c). They are typically wide and short-crested and their origin is the merging of a crescentic bar into the beach as has been described previously. Therefore, their spacing [math]L[/math] is the spacing of the pre-existing crescentic bar. As in the case of crescentic bars, TBR bars also show strong and narrow rip currents flowing seaward in the troughs and wider and weaker onshore flows over the crests. They can be either shore-normal or down-current oriented if the wave incidence is oblique.


Medium Energy Finger Bars

They have been observed in open microtidal beaches under medium-energy conditions [12][9] and they always coexist with shore-parallel (or crescentic) bars. They are thin and elongated (hence finger bars) in contrast with the wider and shorter TBR bars. They are ephemeral (residence time from 1 day to 1 month), attached to the low-tide shoreline or, occasionally, to the shore-parallel bar. They are linked to the presence of alongshore wave driven current and they are up-current oriented. Their spacing is in the range [math]L \approx[/math] 15 -200 m. It seems that some medium energy finger bars show up in Figure 3d.


Long Finger Bars

Figure 4. Long transverse finger bars at Horn Island, Mississippi, USA. Geographical coordinates: [math]30^{\circ} 44' 44''[/math] N, [math]88^{\circ} 41' 17''[/math] W. Wavelength [math]L \approx[/math] 100-150 m (Source: Google Earth).

They are persistent features in low to medium energy beaches without shore-parallel bars and whose foreshore is a very flat terrace [13] [14][15][16][17]. They are characterized by long crests which are typically larger than the alongshore spacing which may vary in the range [math] L \approx[/math] 10 -500 m. The incident wave focusing by the bars caused by topographic refraction seems to be an essential process to them. Although they are most often observed on microtidal beaches, they may also exist on meso and macrotidal coasts [18][10]. We group in this class both the 'large-scale finger bars' and the 'low-energy finger bars' types of [10]. Figures 2b and 4 show some examples.








Large-scale shoreline features

Figure 5. Shoreline sand waves at the Gulf of Finland, Russia. Geographical coordinates: [math]59^{\circ} 57' 22''[/math] N, [math]29^{\circ} 33' 53''[/math] E. Wavelength increasing down-drift from [math]L \approx[/math] 200 m to 1100 m (Source: Google Earth, image from TerraMetrics and GeoEye).

This type is difficult to define and probably includes a number of distinct classes, which are very different in morphology, size and involved physical processes. We define them here as being associated to processes at a length scale larger than the surf zone width, [math]L \gg X_b[/math]. They include shoreline undulations called shoreline sand waves, cuspate forelands and sandy spits [19] (see Figures 2d, e and 5). On low energy shores where [math]X_b[/math] is very small, [math]L[/math] can be [math]\approx[/math] O(100 m), in the same range than megacusps on open ocean beaches. However, large-scale shoreline features can also be very large, up to tens of km, on these ocean shores. An important characteristic is that they are typically linked to similar undulations in the bathymetric contours beyond the surf zone into the shoaling zone, sometimes up to considerable depths [20]. Because of the large length and time scales involved in their dynamics, it is often difficult to ascertain whether they are self-organized or they are forced by offshore bathymetric anomalies or by geological constraints. When there is a dominant littoral drift they tend to migrate down-drift.








Feedback mechanisms

We here describe the main feedback mechanisms that have been identified as potential drivers for self-organized shoreline features.


Surf zone: bedsurf mechanism

Figure 6. Bed-surf feedback mechanism based on the rip-current circulation in the surf zone. The yellow colour indicates emerged or submerged shallower areas, blue colour indicates submerged deeper areas. The lower/higher density of brown spots indicate the lower/higher concentration of suspended sediment. The blue lines with arrows indicate the depth averaged currents.

Let us assume a shore-parallel bar with alternating shallows and deeps or channels on its crest (see Figure 6). The breaking is more intense over the shallows so that there is more wave-induced sea level setup shoreward of them. This creates currents flowing alongshore from the areas shoreward of the shallows to the areas shoreward of the channels. In this way, a rip current circulation flowing seaward at the channels and shoreward at the shallows is originated. Then, let us consider the sediment transported in suspension by the current. Since the larger waves break more offshore and the wave height is gradually reduced onshore, the maximum suspended concentration (i.e., sediment load induced by wave breaking) will therefore occur offshore. Then, the current flowing shoreward at the shoals will carry a lot of sediment into places where the wave agitation is weak and the equilibrium suspended sediment concentration is low. Therefore, the sediment will settle down and sediment deposition will occur at the shoals. On the contrary, the water flowing seaward along the rip channels from the inner surf zone, where the sediment load is weak, will carry small sediment concentrations to places where the wave agitation is high allowing larger concentrations. Therefore, sediment will be picked-up and the channel will be eroded. As a result, the circulation induced by the morphology will bring sediment from the channels into the shoals, i.e., will reinforce the morphology so that a positive feedback will occur. This is the so-called bed-surf mechanism. It was first described in these terms by Falques et al. [21] but was earlier implicitly included in the modelling studies by Hino [22] and Deigaard et al. [23]. The latter paper showed that the bedsurf mechanism can explain the formation of a crescentic bar out of a shore-parallel bar. Numerous subsequent modelling studies have confirmed it in different conditions and with different models [24] [25][26] [27] [28] [29] [30]}. It has been tested in a wave-tank experiment by Michallet et al. [31].

One could argue that in order that the positive feedback occurs, the rhythmic morphology should be already there at the beginning so that the question of where it comes from would remain. This issue is solved by the instability theory which can be sketched as follows. The initial configuration can be assumed as the superposition of a featureless reference morphology (alongshore uniform) plus a perturbation. Then, the perturbation can be expanded as a superposition of normal modes encompassing all alongshore wavelengths. If the amplitude of the perturbation is small enough each mode will evolve separately due to linearity of the governing equations. Thus the feedback can occur for each mode. Depending on their shape and wavelength, some modes will lead to a negative feedback and others to a positive feedback. The most efficient in causing positive feedback will grow faster in time and will eventually dominate the dynamics imprinting its shape and its wavelength, [math]L[/math], on the emerging morphology. The fundamentals of instability theory to explain self-organized coastal features is presented in a comprehensive manner in [32] and in Stability models. A more detailed formulation can be found in [33] and an application example can be seen in [21].

The bedsurf mechanism can also work in a similar way in absence of shore-parallel bars and it can induce the formation of transverse bars [34]. In this case the circulation consists of shoreward flow over the bars and seaward flow at the rip channels which are the troughs in between the bars. This type of coupled morphology and circulation in absence of any shore-parallel bar has been observed, for example, in Monterey Bay, CA (US) [8] [35].


Surf zone: bedflow mechanism

Figure 7. Bed-flow feedback mechanism associated to the wave driven longshore current in the surf zone. It can be based either on the shoreward deflection of the current by down-current oriented bars (a) or on the seaward deflection of the current by up-current oriented bars (b). Colours, brown spots, blue lines and arrows have the same meaning as in Figure 6.

It is well known that a current flowing over a sandy bed can de-stabilize the flat bed and originate a variety of bedforms as ripples, dunes, antidunes, sand waves, bars, sand ridges, etc. Falques et al. [36] examined how the wave-driven longshore current in case of oblique wave incidence could generate rhythmic bars in the surf zone following the analogy with alternate bars in rivers. Following this analogy, the gradients in wave breaking caused by the rhythmic bars (the essential driver of bed-surf mechanism) were ignored and the counterpart of river alternate bars in the nearshore was found. The corresponding feedback mechanism was called bedflow mechanism. In contrast with the bedsurf mechanism, where the differential breaking is essential but there is no longshore current, the current is essential for the bedflow mechanism but differential breaking is ignored. While bedsurf mechanism alone can be realistic in the surf zone (in case of normal wave incidence), bedflow mechanism is not because the current is generated by oblique wave incidence in which case the differential breaking is also present. Still, the bedflow mechanism has been conceptually important since it points to the feedbacks essentially associated to the longshore current in the surf zone.

In order to analyze the possible feedbacks driven by the longshore current in a more realistic way, the models describing the bedsurf mechanism have been extended to account for the differential breaking, therefore mixing bedflow and bedsurf mechanisms [37] [34] [38]}. It has been found that there are indeed two possible feedbacks between oblique bars and the wave-driven longshore current (see Figure 7).

In case of down-current oriented bars it is found that the current is deflected onshore over the bars and offshore at the troughs as a result of mass conservation, current inertia, friction and differential breaking (so with much more complexity than in case of bedsurf mechanism alone). Then, if we assume that the sediment concentration is maximum at the breaking line and decreases onshore, by the same reason explained in the previous section, there will be sediment deposition over the bars and erosion at the channels, hence a positive feedback (Figure 7a).

For up-current oriented bars the current is deflected in the opposite way, offshore over the bars, onshore at the channels. Therefore, if there is a maximum in concentration at the breaking line, the feedback is negative. Only if there is a peak of suspended concentration near the shoreline and a decreasing concentration in the inner surf zone, the feedback can be positive in the inner surf zone (Figure 7b). This is possible thanks to the turbulent bores propagating onshore from the breaking line and has been proved as a possible origin of the medium energy finger bars [38].

Surf-shoaling zones: wave energy mechanism

Figure 8. Feedback mechanisms between shoreline undulations and waves involving both the surf and the shoaling zones. Wave incidence from the left. The blue lines with arrows indicate the wave rays. The brown arrows indicate the larger or smaller total sediment transport rate, [math]Q[/math]. A crest (C) is shown along with the two nearest embayments (E). The areas where sediment excess (deposition) or deficit (erosion) occur are indicated. The wave-energy mechanism which is based on the differences in wave crest stretching between up-drift and down-drift of C is shown. The larger/smaller wave height, [math]H_b[/math], causing the gradients in [math]Q[/math], is indicated.

The length scales at which bedsurf and bedflow mechanisms operate and rhythmic surf zone bars and megacusps emerge are comparable to the surf zone width, [math]X_b[/math], so typically tens to hundreds of m. The time scales involved are of hours to days. Therefore, if we are interested in the behavior of a sandy coast at time scales of years and length scales [math]\gg X_b[/math], i.e., km's, it is reasonable to rely on averages where the internal dynamics of the surf zone is filtered out. In case of oblique wave incidence this can be done by considering the total cross-shore integrated alongshore sediment transport rate, [math]Q[/math] (m[math]^3[/math]/s) and looking at its alongshore gradients. Where there is convergence of [math]Q[/math] there is overall sand accumulation and the shoreline progrades and where there is divergence of [math]Q[/math] there is overall sand deficit and the shoreline retreats. The sediment transport rate [math]Q[/math] can be evaluated with semi-empirical formulae in terms of the wave characteristics at breaking. Let us assume oblique wave incidence on an undulating coastline with an angle [math]\theta_b[/math] at breaking with respect to the mean shoreline trend (absolute incidence angle). If [math]\phi[/math] is the local orientation of the shoreline with respect to its mean trend, the wave incidence angle with respect to the local shore normal is [math]\alpha_b = \theta_b - \phi[/math] (relative incidence angle). Then, if [math]H_b[/math] is the wave height at breaking, [math]Q[/math] can typically be cast into

[math] Q = f(H_b) \Psi(\alpha_b) , \qquad (1)[/math]

where both [math]f,\Psi[/math] are increasing functions (in case of [math]\Psi[/math] it is increasing only for [math]\theta_b \lt 45^{\circ}[/math], but due to wave refraction [math]\theta_b[/math] is rarely [math]\gt 45^{\circ}[/math]). A well-known example is the CERC formula [39].

Having all this in mind, we first examine how large scale ([math]L \gg X_b[/math]) shoreline undulations cause gradients in [math]H_b[/math] that cause, in turn, gradients in [math]Q[/math]. Because of topographic wave refraction the wave crests stretch so that the wave energy undergoes dispersion and wave height tends to decrease (Figure 8). This effect is more pronounced as more intense is the wave ray bending. A shoreline undulation is commonly linked to similar undulations in the bathymetric contours up to certain depth, [math]D_c[/math]. This affects wave refraction so that the ray bending will be more pronounced at the down-drift sides of the headlands of the undulation than at the up-drift sides. This will induce less wave height at the down-drift sides than at the up-drift with the result that [math]Q[/math] will decrease moving from up-drift to down-drift making the headlands prograde (Figure 8). Similarly, divergence of [math]Q[/math] will occur at the embayments so that the shoreline will retreat there. Thus, a positive feedback is originated. We call it wave-energy mechanism [40]. It is important to stress that the feedback is essentially based on the alteration of wave refraction by the perturbed depth contours before wave breaking. Thus, it takes place at the surf and shoaling zones together. Consequently, to sustain the feedback, the bathymetric undulations must follow the shoreline undulations: moving offshore when the shoreline progrades and onshore when it retreats. This process is not simultaneous to the morphological changes driven by [math]Q[/math], which take place at the surf zone or near. It is accomplished gradually by the wave driven cross-shore transport and both, longshore transport and cross-shore transport work together only on average at large time scales. Most of the modelling studies that have explored this mechanism have considered an instantaneous link between shoreline and bathymetry on the basis of the large time scales [19] [41] [42] [43], but a study where this assumption was lifted out showed that the mechanism does not depend essentially on it [44]. The role of wave-energy mechanism as a potential driver of large scale shoreline features will be discussed in the last section.

We must also mention that the distribution of wave energy along a shoreline undulation is also affected by wave focusing by the headlands and de-focusing by the embayments. This can alter and inhibit the wave-energy mechanism as it tends to move the maximum in wave energy down-drift, near the headland. In fact, it becomes always dominant for small enough wavelengths and controls the characteristic wavelength of the emerging shoreline features [45].


Surf-shoaling zones: wave angle mechanism

Figure 9. Feedback mechanisms between shoreline undulations and waves involving both the surf and the shoaling zones. Left: Definition of absolute and relative wave incidence angles, [math]\theta[/math] and [math]\alpha=\theta - \phi[/math], respectively. The straight brown line represents the local shoreline orientation. Right: The wave-angle mechanism which is based on the differences in relative wave-angle between up-drift and down-drift of C is shown. The larger/smaller relative wave angle, [math]\alpha_b = \theta_b - \phi[/math], causing the gradients in [math]Q[/math], is indicated. As in Figure 8, the wave incidence is from the left and the symbols have the same meaning. An example where the wave-angle mechanism induces a positive feedback is presented.

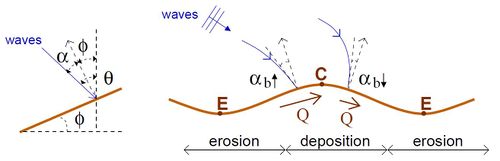
Let us now examine how a large scale undulating coastline causes gradients in [math]Q[/math] through the gradients in relative wave angle, [math]\alpha_b = \theta_b - \phi [/math]. We first consider the gradients in [math]\theta_b[/math] (ignoring for a while the gradients in [math]\phi[/math]). As has been explained in the previous section, wave refraction is more intense at the down-drift sides of headlands than at the up-drift sides. Thus, [math]\theta_b[/math] is smaller at the down-drift side and so does [math]Q[/math]. Therefore, this effect makes [math]Q[/math] decrease moving from the up-drift to the down-drift sides with the result that it causes sediment accumulation and progradation of the headlands. Just the contrary happens at the embayments, so that the shoreline tends to retreat. Thus, the gradients in absolute wave angle, [math]\theta_b[/math], always induce a positive feedback between waves and morphology.

However, the local shoreline angle, [math]\phi[/math], counteracts this positive feedback. Indeed, the maximum in [math]\phi[/math] is located up-drift of each headland and the minimum (maximum magnitude with minus sign) is located down-drift of the headland. This tends to locate the minimum in relative angle, [math]\alpha_b = \theta_b - \phi [/math], at the up-drift side of the headland and the maximum at the down-drift side, contrarily to the effect of [math]\theta_b[/math]. Therefore, the gradients in [math]\phi[/math] counteract the positive feedback originated by the gradients in [math]\theta_b[/math]. We call the interplay of both effects wave-angle mechanism [40]. Which effect is dominant, i.e., whether the wave-angle mechanism induces a positive or a negative feedback depends on a number of factors: the cross-shore mean bathymetric profile, the depth of closure, [math]D_c[/math] and the wave conditions (angle, height and period) [40]. It also depends on the shape of the bathymetric perturbation associated to the shoreline undulations, so that a positive feedback requires bathymetric undulations with larger amplitude than the shoreline undulations [46]. Figure 9 illustrates a case where the feedback resulting from the gradients in [math]\alpha_b[/math] is positive.

Instabilities driven by the litoral drift

As it has been seen in the previous sections, the gradients in [math]Q[/math] are governed by the wave-energy and wave-angle mechanisms. For large enough wavelength, [math]L[/math], the wave-energy always induces a positive feedback. However, the feedback induced by the wave-angle can be either positive or negative. The most common situation is the latter one and, in this case, it turns out that the resulting feedback is negative for [math]\theta \lt \theta_c[/math] and positive for [math]\theta \gt \theta_c[/math], where the wave angles are evaluated at [math]D_c[/math]. The threshold angle, [math]\theta_c[/math], ranges between [math]40^{\circ}[/math] and [math]90^{\circ}[/math]. This instability is called High-angle wave instability (HAWI) and it has been hypothesized that it is the origin of a number of large scale features like shoreline sand waves, cuspate forelands and sandy spits [19] [47] [48] [49] [50] [42] [51]. In case that the bathymetric undulations have larger amplitude than the shoreline undulations, for low gradient shorefaces and large enough [math]D_c[/math], the wave-angle mechanism can induce a very weak negative feedback or even a positive one. In this case, the critical angle [math]\theta_c[/math] can be very low or even [math]0[/math], which means that the shoreline can be unstable for very low wave angles. This situation was called Low-angle wave instability (LAWI) by Idier et al [52] and has been extensively studied by Falques [40], where it is shown that the shoreline sand waves observed at Holmslands Tange (west Danish coast) might be jointly driven by both wave-energy and wave-angle mechanisms.


Acknowledgments

This article has been written within the project CTM2015-66225-C2-1-P, which is funded by the Spanish Government and cofounded by the E.U. (FEDER). Useful advice and comments by Prof. J. Dronkers as well as pictures provided by Prof. A.D. Short are gratefully acknowledged.


Related articles

Stability models

Beach Cusps

Sand transport

Sediment transport formulas for the coastal environment

Swash zone dynamics


References

  1. ↑ Coco, G. and A.B. Murray (2007), Patterns in the sand: From forcing templates to self-organization, Geomorphology, 91, 271-290
  2. ↑ van Enckevort, I. M. G., B. G. Ruessink, G. Coco, K. Suzuki, I. L. Turner, N. G. Plant, and R. A. Holman (2004), Observations of nearshore crescentic sandbars, J. Geophys. Res., 109 (C06028), doi:10.1029/2003JC002214
  3. ↑ Castelle, B., P. Bonneton, H. Dupuis, and N. Senechal (2007), Double bar beach dynamics on the high-energy meso-macrotidal french aquitanian coast: A review, Mar. Geol., 245, 141-159
  4. ↑ Ribas, F., A. Falques, H. E. de Swart, N. Dodd, R. Garnier, and D. Calvete (2015), Understanding coastal morphodynamic patterns from depth-averaged sediment concentration, Rev. Geophys., 53, doi:10.1002/2014RG000457
  5. ↑ MacMahan, J. H., E. B. Thornton, and A. J. H. M. Reniers (2006), Rip current review, Coastal Eng., 53, 191-208
  6. ↑ Dalrymple, R. A., J. H. MacMahan, A. J. H. M. Reniers, and V. Nelko (2011), Rip currents, Annu. Rev. Fluid Mech., 43, 551-581
  7. ↑ Shepard, F. P. (1952), Revised nomenclature for depositional coastal features, Bull. Am. Assoc. Petrol. Geol., 36 (10), 1902-1912
  8. ↑ 8.0 8.1 Thornton, E. B., J. MacMahan, and A. H. Sallenger (2007), Rip currents, mega-cusps, and eroding dunes, Marine Geology, 240, 151 167
  9. ↑ 9.0 9.1 Ribas, F., and A. Kroon (2007), Characteristics and dynamics of surfzone transverse finger bars, J. Geophys. Res., 112 (F03028), doi:10.1029/2006JF000685 Cite error: Invalid <ref> tag; name "R1" defined multiple times with different content
  10. ↑ 10.0 10.1 10.2 10.3 10.4 Pellon, E., R. Garnier, and R. Medina (2014), Intertidal finger bars at El Puntal, Bay of Santander, Spain: observation and forcing analysis, Earth Surface Dynamics, 2, 349-361
  11. ↑ Wright, L. D., and A. D. Short (1984), Morphodynamic variability of surf zones and beaches: A synthesis, Mar. Geol., 56, 93-118
  12. ↑ Konicki, K. M., and R. A. Holman (2000), The statistics and kinematics of transverse bars on an open coast, Mar. Geol., 169, 69-101
  13. ↑ Evans, O. F. (1938), The classication and origin of beach cusps, J. Geology, 46, 615-627
  14. ↑ Niederoda, A. W., and W. F. Tanner (1970), Preliminary study on transverse bars, Mar. Geol., 9, 41-62
  15. ↑ Falques, A. (1989), Formacion de topografia ritmica en el Delta del Ebro, Revista de Geofisica, 45 (2), 143-156
  16. ↑ Bruner, K. R., and R. A. Smosna (1989), The movement and stabilization of beach sand on transverse bars, Assateague Island, Virginia, J. Coastal Res., 5 (3), 593-601
  17. ↑ Gelfenbaum, G., and G. R. Brooks (2003), The morphology and migration of transverse bars off the west-central Florida coast, Mar. Geol., 200, 273-289
  18. ↑ Levoy, F., E. J. Anthony, O. Monfort, N. Robin, and P. Bretel (2013), Formation and migration of transverse bars along a tidal sandy coast deduced from multi-temporal lidar datasets, Mar. Geol., 342, 39-52
  19. ↑ 19.0 19.1 19.2 Ashton, A., A. B. Murray, and O. Arnault (2001), Formation of coastline features by large-scale instabilities induced by high-angle waves, Nature, 414, 296-300
  20. ↑ Kaergaard, K., J. Fredsoe, and S. B. Knudsen (2012), Coastline undulations on the West Coast of Denmark: Offshore extent, relation to breaker bars and transported sediment volume, Coastal Eng., 60, 109-122
  21. ↑ 21.0 21.1 Falques, A., G. Coco, and D. A. Huntley (2000), A mechanism for the generation of wave-driven rhythmic patterns in the surf zone, J. Geophys. Res., 105 (C10), 24,071-24,088
  22. ↑ Hino, M. (1974), Theory on formation of rip-current and cuspidal coast, in Coastal Eng. 1974, pp. 901-919, Am. Soc. of Civ. Eng.
  23. ↑ Deigaard, R., N. Droenen, J. Fredsoe, J. H. Jensen, and M. P. Joergensen (1999), A morphological stability analysis for a long straight barred coast, Coastal Eng., 36 (3), 171-195
  24. ↑ Reniers, A. J. H. M., J. A. Roelvink, and E. B. Thornton (2004), Morphodynamic modeling of an embayed beach under wave group forcing, J. Geophys. Res., 109 (C01030), doi:10.1029/2002JC001586
  25. ↑ Ranasinghe, R., G. Symonds, K. Black, and R. Holman (2004), Morphodynamics of intermediate beaches: A video imaging and numerical modelling study, Coastal Eng., 51, 629-655
  26. ↑ Calvete, D., N. Dodd, A. Falques, and S. M. van Leeuwen (2005), Morphological development of rip channel systems: Normal and near normal wave incidence, J. Geophys. Res., 110 (C10006),Doi:10.1029/2004JC002803
  27. ↑ Garnier, R., D. Calvete, A. Falques, and N. Dodd (2008), Modelling the formation and the long-term behavior of rip channel systems from the deformation of a longshore bar, J. Geophys. Res., 113 (C07053), doi:10.1029/2007JC004632
  28. ↑ Smit, M., A. Reniers, B. Ruessink, and J. Roelvink (2008), The morphological response of a nearshore double sandbar system to constant wave forcing, Coastal Eng., 55, 761-770
  29. ↑ Orzech, M. D., A. J. H. M. Reniers, E. B. Thornton, and J. H. MacMahan (2011), Mega-cusps on rip channel bathymetry: Observations and modeling, Coastal Eng., 58, 890907
  30. ↑ Castelle, B., and G. Coco (2012), The morphodynamics of rip channels on embayed beaches, Cont. Shelf Res., 43, 10-23
  31. ↑ Michallet, H., B. Castelle, E. Barth elemy, C. Berni, and P. Bonneton (2013), Physical modeling of three-dimensional intermediate beach morphodynamics, J. Geophys. Res., 118, 1-15, doi:10.1002/jgrf.20078
  32. ↑ Dronkers, J. (2016), Dynamics of Coastal Systems second edition, World Scientific Publ. Co., Singapore
  33. ↑ Dodd, N., P. Blondeaux, D. Calvete, H. E. de Swart, A. Falques, S. J. M. H. Hulscher, G. Rozynski, and G. Vittori (2003), The use of stability methods in understanding the morphodynamical behavior of coastal systems, J. Coastal Res., 19 (4), 849-865
  34. ↑ 34.0 34.1 Garnier, R., D. Calvete, A. Falques, and M. Caballeria (2006), Generation and nonlinear evolution of shore-oblique/transverse sand bars, J. Fluid Mech., 567, 327-360 Cite error: Invalid <ref> tag; name "G6" defined multiple times with different content
  35. ↑ MacMahan, J. H., E. B. Thornton, A. J. H. M. Reniers, T. P. Stanton, and G. Symonds (2008), Low-energy rip currents associated with small bathymetric variations, Marine Geology, 255, 156-164
  36. ↑ Falques, A., A. Montoto, and V. Iranzo (1996), Bedflow instability of the longshore current, Cont. Shelf Res., 16 (15), 1927-1964
  37. ↑ Ribas, F., A. Falques, and A. Montoto (2003), Nearshore oblique sand bars, J. Geophys. Res., 108 (C43119), doi:10.1029/2001JC000985
  38. ↑ 38.0 38.1 Ribas, F., H. E. de Swart, D. Calvete, and A. Falques (2012), Modeling and analyzing observed transverse sand bars in the surf zone, J. Geophys. Res., 117 (F02013), doi:10.1029/2011JF002158
  39. ↑ Komar, P. D., and R. A. Holman (1986), Coastal processes and the development of shoreline erosion, Annual Review Earth and Planetary Sciences, 14, 237-265
  40. ↑ 40.0 40.1 40.2 40.3 Falques, A., F. Ribas, D. Idier, and J. Arriaga (2017), Formation mechanisms for self-organized km-scale shoreline sand waves, J. Geophys. Res., 10.1002/2016JF003964, in press
  41. ↑ Falques, A., and D. Calvete (2005), Large scale dynamics of sandy coastlines. Diffusivity and instability, J. Geophys. Res., 110 (C03007), doi:10.1029/2004JC002587
  42. ↑ 42.0 42.1 Kaergaard, K., and J. Fredsoe (2013a), Numerical modeling of shoreline undulations part 1: Constant wave climate, Coastal Eng., 75, 64-76
  43. ↑ Kaergaard, K., and J. Fredsoe (2013b), Numerical modeling of shoreline undulations part 2: Varying wave climate and comparison with observations, Coastal Eng., 75, 77-90
  44. ↑ van den Berg, N., A. Falques, and F. Ribas (2012), Modelling large scale shoreline sand waves under oblique wave incidence, J. Geophys. Res., 117 (F03019), doi:10.1029/2011JF002177
  45. ↑ van den Berg, N., A. Falques, F. Ribas, and M. Caballeria (2014), On the wavelength of self-organized shoreline sand waves, J. Geophys. Res. Earth Surf., 119, 665-681, doi:10.1002/2013JF002751
  46. ↑ Idier, D., A. Falques, J. Rohmer, and J. Arriaga (2017), Self-organized kilometre-scale shoreline sandwave generation: sensitivity to model and physical parameters, J. Geo-phys. Res., submitted
  47. ↑ Ashton, A., and A. B. Murray (2006), High-angle wave instability and emergent shoreline shapes: 2. Wave climate analysis and comparisons to nature, J.Geophys.Res., 111, F04,012,doi:10.1029/2005JF000,423
  48. ↑ Falques, A. (2006), Wave driven alongshore sediment transport and stability of the Dutch coastline, Coastal Eng., 53, 243-254
  49. ↑ Medellin, G., A. Falques, R. Medina, and M. Gonz alez (2009), Sand waves on a low-energy beach at 'El Puntal' spit, Spain: Linear Stability Analysis, J. Geophys. Res., 114 (C03022), doi:10.1029/2007JC004426
  50. ↑ Ashton, A. D., A. B. Murray, R. Littlewood, D. A. Lewis, and P. Hong (2009), Fetch-limited self-organization of elongate water bodies, Geology, 37, 187-190
  51. ↑ Idier, D., and A. Falques (2014), How kilometric sandy shoreline undulations correlate with wave and morphology characteristics: preliminary analysis on the Atlantic coast of Africa, Advances in Geosciences, 39, 55-60, doi:10.5194/adgeo-39-55-2014
  52. ↑ Idier, D., A. Falques, B. G. Ruessink, and R. Garnier (2011), Shoreline instability under low-angle wave incidence, J. Geophys. Res., 116 (F04031), doi:10.1029/2010JF001894


The main authors of this article are Albert Falques, Francesca Ribas and Daniel Calvete
Please note that others may also have edited the contents of this article.
Citation: Albert Falques; Francesca Ribas; Daniel Calvete ; (2017): Rhythmic shoreline features. Available from http://www.coastalwiki.org/wiki/Rhythmic_shoreline_features [accessed on 23-11-2024]
Retrieved from "https://www.coastalwiki.org/w/index.php?title=Rhythmic_shoreline_features&oldid=73161"