Difference between revisions of "Measurements of biodiversity"
Dronkers J (talk | contribs) |
Dronkers J (talk | contribs) |
||
| Line 154: | Line 154: | ||
===Functional diversity=== | ===Functional diversity=== | ||
| + | Functional diversity is concerned with the roles that species exert in a community. Functional diversity (presence of diverse [[functional groups]]) is a better indicator of ecosystem resilience than biodiversity (based on species richness and abundances), although a positive correlation generally exists<ref>McCann, K. S. 2000. The diversity-stability debate. Nature 405: 228–233</ref>. This can be attributed to the greater number of [[functional groups]] found in richer [[assemblage]]s (see also [[Resilience and resistance]]). Functional diversity increases the overall productivity of an ecosystem by allowing for more complementary functions and effective niche occupation<ref>Cardinale, B. J., Wright, J. P. and Cadotte, M. W., Carroll, I.T., Hector, A., Srivastava, D.S., Loreau, M. and Weis, J.J. 2007. Impacts of plant diversity on biomass production increase through time because of species complementarity. PNAS 104: 18123–18128</ref>, see [[Functional diversity in marine ecosystems]]. | ||
| − | + | Petchey and Gaston <ref> Petchey O.L. and Gaston K.J. 2002. Functional diversity (FD), species richness and community composition. Ecology letters Vol. 5 (3): 402-411</ref> proposed a method for quantifying functional diversity. It is based on total branch length of a [[dendrogram]], which is constructed from species trait values. One important consideration is that only those traits linked to [[ecosystem functioning]] are used. Thus a study focusing on bird-mediated seed dispersal would exclude traits such as plumage color that are not related to this function, but traits such as beak size and shape should be included. With standard clustering algorithms a dendrogram is then constructed. For example, a community with five species with different traits will have a higher functional diversity than a community of equal richness but where the species are functionally similar. See also the article [[Functional diversity in marine ecosystems]]. | |
| Line 303: | Line 304: | ||
The characterization of ecosystems by one or a few numbers is an extreme simplification of their real complexity. An often voiced criticism is therefore that ecosystem management cannot be guided by biodiversity indices alone<ref>Karydis, M. 2022. Critique on Ecological Methodologies Used in Water Quality Studies and Coastal Management: A Review. J. Mar. Sci. Eng. 10, 701</ref>. Biodiversity indices are proxies of biodiversity. There is no single 'right' indicator<ref>Bartkowski, B., Lienhoop, N. and Hansjurgens, B. 2015. Capturing the complexity of biodiversity: A critical review of economic valuation studies of biological diversity. Ecological Economics 113: 1-14</ref>. Biodiversity indices embody certain aspects of ecosystems, but are insensitive to many others. The interpretation of biodiversity indices as a characteristic of ecosystems is therefore problematic. An unequivocal relationship with environmental conditions is often lacking. The interpretation of results can be profoundly altered depending on the choice of the biodiversity index<ref>Morris, E.K., Caruso, T., Buscot, F., Fischer, M., Hancock, C., Maier, T.S., Meiners, T., Muller, C., Obermaier, E., Prati, D., Socher, S.A., Sonnemann, I., Waschke, N., Wubet, T., Wurst, S. and Rillig, M.C. 2014. Choosing and using diversity indices: insights for ecological applications from the German Biodiversity Exploratories. Ecology and Evolution 4: 3514–3524</ref>. Biodiversity indices are therefore considered too abstract and unsuitable for public and political communication. | The characterization of ecosystems by one or a few numbers is an extreme simplification of their real complexity. An often voiced criticism is therefore that ecosystem management cannot be guided by biodiversity indices alone<ref>Karydis, M. 2022. Critique on Ecological Methodologies Used in Water Quality Studies and Coastal Management: A Review. J. Mar. Sci. Eng. 10, 701</ref>. Biodiversity indices are proxies of biodiversity. There is no single 'right' indicator<ref>Bartkowski, B., Lienhoop, N. and Hansjurgens, B. 2015. Capturing the complexity of biodiversity: A critical review of economic valuation studies of biological diversity. Ecological Economics 113: 1-14</ref>. Biodiversity indices embody certain aspects of ecosystems, but are insensitive to many others. The interpretation of biodiversity indices as a characteristic of ecosystems is therefore problematic. An unequivocal relationship with environmental conditions is often lacking. The interpretation of results can be profoundly altered depending on the choice of the biodiversity index<ref>Morris, E.K., Caruso, T., Buscot, F., Fischer, M., Hancock, C., Maier, T.S., Meiners, T., Muller, C., Obermaier, E., Prati, D., Socher, S.A., Sonnemann, I., Waschke, N., Wubet, T., Wurst, S. and Rillig, M.C. 2014. Choosing and using diversity indices: insights for ecological applications from the German Biodiversity Exploratories. Ecology and Evolution 4: 3514–3524</ref>. Biodiversity indices are therefore considered too abstract and unsuitable for public and political communication. | ||
| − | Biodiversity indices depend on the way they are determined. Since the statistical distribution of samples is generally not known, it is difficult to estimate the accuracy of a given index value<ref name=BS>Barrantes, G. and Sandoval, L. 2009. Conceptual and statistical problems associated with the use of diversity indices in ecology. Rev. Biol. Trop. 57: 451-60</ref>. As discussed earlier, the sample size and the thoroughness of the sampling play an important role<ref name=S68/>. The sampling of species with a patchy distribution pattern easily leads to flawed (underestimated or overestimated) numbers. Tiny species and rare species with an important ecosystem role are often not fully included or even completely missed. | + | Biodiversity indices depend on the way they are determined. Since the statistical distribution of samples is generally not known, it is difficult to estimate the accuracy of a given index value<ref name=BS>Barrantes, G. and Sandoval, L. 2009. Conceptual and statistical problems associated with the use of diversity indices in ecology. Rev. Biol. Trop. 57: 451-60</ref>. As discussed earlier, the sample size and the thoroughness of the sampling play an important role<ref name=S68/>. The sampling of species with a patchy distribution pattern easily leads to flawed (underestimated or overestimated) numbers. Tiny species and rare species with an important ecosystem role are often not fully included or even completely missed. Another issue is related to defining the spatial boundaries of an ecosystem. It can be argued that a natural community is an open system with nothing approaching a fixed number of species<ref name=P74/>. |
| + | |||
| + | A more fundamental critics relates to the premise of most biodiversity indices that all species are equal (this critics holds to a lesser extent for functional diversity indices). The identity of species and their role in the community is lost in the biodiversity indices<ref name=BS/>. Often a few particular species can have an impact on the community or ecosystem that far exceeds their relative abundance or biomass. Such '''keystone species''' can fulfill different roles in [[ecosystem functioning]], for example: | ||
| + | *Controlling the abundance of species at lower trophic levels (e.g. apex predators, see [[Trophic cascade]]) | ||
| + | *Creating microhabitats for other species by activities such as burrowing, scraping, sediment retention, sheltering, shading, … (eco-engineer function) | ||
| + | *Transforming chemicals into compounds that can be assimilated by other species (e.g. nitrogen fixation) | ||
| + | *Rare species that form a reservoir of functional and genetic diversity, contributing to the stability and resilience of the ecosystem | ||
| + | An assessment of ecosystem health or resilience cannot be based on biodiversity indices alone, but has to consider the specific role of keystone species<ref>Power, M.E., Tilman, D., Estes, J.A., Menge, B.A., Bond, W.J., Mills, L.S., Daily, G., Castilla, J.C., Lubchenco, J. and Paine, R.T. 1996. Challenges in the Quest for Keystones. BioScience 46: 609-620</ref>. | ||
Despite the above criticisms, biodiversity indices, and in particular the analysis of species abundance distributions, have proven useful in practice to act as an early warning tool for the effects of disturbance on ecological communities, and to provide a means for measuring the implementation of regulations for ecological management<ref name=MW/>. | Despite the above criticisms, biodiversity indices, and in particular the analysis of species abundance distributions, have proven useful in practice to act as an early warning tool for the effects of disturbance on ecological communities, and to provide a means for measuring the implementation of regulations for ecological management<ref name=MW/>. | ||
Revision as of 16:31, 15 December 2024
Many definitions of the concept 'biodiversity' (shorthand of biological diversity) have been proposed. However, the concept can be interpreted in so many equally valid ways, that no single definition can be considered most appropriate.[1] Consequently, there is no unique measure of biodiversity. Ecosystem characteristics that highlight different aspects of biodiversity are numerous, for example the total number of different species occurring in a particular site and the number of individuals (abundance) in each species. For various characteristics of biological diversity, 'objective' indices have been developed that can be estimated from field observations. This article discusses the most commonly used biodiversity indices.
Contents
- 1 Different types of biodiversity indices
- 2 Measuring biodiversity versus valuing biodiversity
- 3 Quantifying biodiversity
- 4 Species-abundance representations[22]
- 5 Species-abundance models[4]
- 6 Sampling issues of species-abundance distributions
- 7 Rarefaction
- 8 Ecosystem health assessment
- 9 Criticism of biodiversity indices
- 10 Appendix Completeness
- 11 Appendix Shannon-Wiener index
- 12 Appendix Hill number of order 1
- 13 Appendix Logseries rank-abundance
- 14 Appendix Geometric model
- 15 Appendix Rarefaction
- 16 List of symbols
- 17 Related articles
- 18 Further reading
- 19 References
Different types of biodiversity indices
The basic idea of a biodiversity index is to obtain a quantitative estimate of biological variability in space or in time that can be used to compare biological entities, composed of diverse components. It is important to distinguish ‘richness’ from ‘diversity’. Diversity usually implies a measure of both species number and ‘equitability’ (or ‘evenness’). Three types of indices can be distinguished:
1. Species richness indices: Species richness is a measure for the total number of the species in a community (examples Fig. 1a). However, complete inventories of all species present at a certain location, is an almost unattainable goal in practical applications.
2. Evenness indices: Evenness expresses how evenly the individuals in a community are distributed among the different species (examples Fig.1b).
3. Taxonomic indices: These indices take into account the taxonomic relation between different organisms in a community. Taxonomic diversity, for example, reflects the average taxonomic distance between any two organisms, chosen at random from a sample. The distance can be seen as the length of the path connecting these two organisms along the branches of a phylogenetic tree.
These three types of indices (richness, evenness, taxonomic) can be used on different spatial scales [2]:
- Alpha diversity refers to diversity within a habitat, community, ecosystem or site, and is usually measured by counting the number of taxa within the ecosystem (usually at species level).
- Beta diversity is defined as the change in species diversity along environmental gradients or between ecosystems; this involves comparing the number of taxa that are unique to each of the ecosystems (change of taxa depending on change of environmental conditions). For example, the diversity of mangroves versus the diversity of seagrass beds.
- Gamma diversity is a measure of the overall diversity of entire landscapes. For example, the diversity within the coastal region of Gazi Bay in Kenia.
If diversity is represented by the number of species [math]S[/math], then beta diversity [math]D_{\beta}[/math] can be defined as the ratio of the total number of species in the landscape [math]S_{\gamma}[/math] and the mean number of species of all the habitats in the landscape [math]\overline{S}_{\alpha}[/math] minus one, [math]D_{\beta} = S_{\gamma} / \overline{S}_{\alpha} – 1 .[/math][2] When all species are present in all ecosystems, beta diversity is null. As species become more distinctive among ecosystems, beta diversity rises; it is maximal when no two ecosystems hold any species in common.
Another measure of (dis)similarity between communities is given by the Jaccard index of species similarity [math]S_J[/math]. This index is defined as
[math]S_J = \Large\frac{S_c}{S_1 + S_2 - S_c}\normalsize , \qquad (1)[/math]
where [math]S_1[/math] and [math]S_2[/math] are the species numbers of communities 1 and 2, and [math]S_c [/math] is the number of species common to both communities. [math]S_J=1[/math] for complete similarity and [math]S_J=0[/math] for complete dissimilarity. The Jaccard similarity index can also be used for analyzing change in community structure along gradients of environmental change[3].
Measuring biodiversity versus valuing biodiversity
Measuring biodiversity is not the same as valuing biodiversity. Valuing biodiversity in terms of ecosystem goods and services depends on the different elements and distribution of biodiversity such as the number and functional attributes of species, taxonomic relatedness of species and distribution of individuals amongst species. For example, measuring biodiversity does not tell whether a community with a high number of species but dominated in terms of abundance by only a few species is more or less valuable than a community with a lower number of species where individuals are distributed rather evenly among species.
Ecosystem biodiversity indices play an important role in signaling changes in the state of ecosystems. Interpreting changes requires further investigation, taking into account other ecosystem features, such as trophic structure, reproductive potential, competitive interaction, etc., in combination with changes in physical and chemical environmental conditions.
Quantifying biodiversity
A leading principle is that 'all species and individuals are considered equal'[4]. This means that different species count in the same way in the indices. No specific weights are assigned to species, except for numbers of individuals per species (species abundances). The same holds for the individuals within a species. The principle of equality implies that diversity indices do not discriminate between species and communities with very different functionalities.
Biodiversity indices are greatly influenced by sampling size and sampling methods used, for example type of gear, screen size, sorting technique, etc. [3]. Single-sample observations can easily be biased. In principle, a number of separate samples have to be taken to check the reproducibility of the results and to derive statistically meaningful estimations of biodiversity.
Completeness [math]C[/math] is an indicator that can be used to estimate the extent to which the size [math]N[/math] of a sample is sufficiently large. It is given by (see #Appendix Completeness)
[math]C = 1 - \sum_{i-1}^S \Big[ \large\frac{n_i}{N}\normalsize \, ( 1 - \large\frac{n_i}{N}\normalsize)^N \Big] \; , \qquad (2)[/math]
where [math]N=[/math] total number of individuals in the sample, [math]S=[/math] the number of species and [math]n_1, n_2, …, n_i, …, n_S[/math] the numbers of individuals (abundancies) in species [math]1, 2, …, i, …, S[/math]. A sample is sufficiently large if [math]C[/math] is close to 1. [5]
Biodiversity indices based on species abundances are not always meaningful. This can be the case when species in an assemblage using the same resource have very different biomasses. Biodiversity indices based on species biomass may then be more relevant than indices based species abundance.[6]
Diversity (richness) indices
Species richness [math]S[/math] is the simplest measure of biodiversity and is just a count of the number of different species in a given area. This measure is strongly dependent on sampling size and effort. Two species richness indices try to account for this problem:
Margalef’s diversity index[7]
[math]D_{Mg} = \Large\frac{S-1}{\ln N}\normalsize , [/math]
where [math]N[/math] = population = the total number of individuals in the sample and [math]S[/math] = the number of species recorded.
Menhinick’s diversity index[8]
[math]D_{Mn} = \Large\frac{S}{\sqrt{N}} \normalsize. [/math]
Despite the attempt to correct for sample size, both measures remain strongly influenced by sampling effort. Nonetheless they are intuitively meaningful indices and can play a useful role in investigations of biological diversity.
Diversity (richness-evenness) indices
Richness and evenness are two independent components of diversity. Diversity indices, combining richness and evenness can be related to information theory: the assumption that the diversity in a natural system can be measured in a way similar to the information contained in a code or message (see #Appendix Shannon-Wiener index).
Shannon-Wiener diversity index
The most widely used diversity index in the ecological literature is the Shannon-Wiener diversity index[9][10], also called 'Shannon entropy' or 'Shannon entropy index'.
The Shannon entropy is given by the expression
[math]H'_{abundance} \equiv H' = -\sum_{i=1}^S p_i \, \ln p_i , \qquad (3)[/math] ,
where [math]p_i[/math] is the probability to find [math]n_i= N p_i[/math] individuals in the [math]i[/math]-th species ([math]\sum_{i=1}^S p_i = 1[/math]). The number of individuals [math]n_i[/math] of species [math]i[/math] is called the abundance of this species. The Shannon entropy is high if there are many species in the sample, each with a similar population number, in which case [math]H' \approx \ln(S)[/math]. If only one species is present, the Shannon entropy is zero. The Shannon-Wiener index actually measures the uncertainty in the species identity of an individual picked at random from the sample.
In practice, the probability [math]p_i[/math] is estimated by counting the number of individuals in a sample, [math]p_i=n_i /N[/math]. It assumes that individuals are randomly sampled from a very large community, and that all species are represented in the sample. A characteristic of the Shannon entropy index is its sensitivity to small changes in the abundance of rare species[11]. The index is biased if rare species are over- or under-represented in the sample, which can easily happen if communities have a patchy distribution.
Diversity can also be based on other ecosystem characteristics than numbers of individuals per species. An example is a Shannon entropy index based on biomass,
[math]H'_{biomass} = -\sum_{i=1}^S p'_i \, \ln p'_i , \qquad (4)[/math] ,
where [math]p'_i[/math] is the probability to find [math]B_i= B p'_i[/math] biomass in the [math]i[/math]-th species ([math]\sum_{i=1}^S p'_i = 1[/math]) and [math]B = \sum_{i=1}^S B_i[/math] is the total biomass of the sample. The biomass Shannon entropy is high if there are many species in the sample, each with a similar biomass.
Brillouin index
Where the randomness of the sample cannot be guaranteed, for example when certain species have a lower or higher probability of being sampled sampled, the Brillouin index[12][10] is a more appropriate form of the information index. It is calculated as follows:
[math]H = \Large\frac{1}{N}\normalsize [ \ln(N!) - \sum_{i=1}^S \ln(n_i !)] , \qquad (5)[/math]
in which [math] n_i != 1 \times 2 \times 3 \times ... \times n_i[/math] and [math]n_i [/math] = the number of individuals in species [math]i[/math] and [math]N=\sum_{i=1}^S n_i[/math] is the total number of individuals in the community. The relation between the Brillouin index and the Shannon-Wiener index is explained in #Appendix Shannon-Wiener index.
Simpson ’s index
One of the best known and earliest evenness measures is the Simpson ’s index[13] which is given by:
[math]\gamma\, = \sum_{i=1}^S p_i^2 . \qquad (6)[/math]
This index is used for large sampled communities. Simpson’s index expresses the probability that any two individuals drawn at random from an infinitely large community belong to the same species. It decreases with increasing species richness. If all species are equally represented in the sample, then [math]p_i=1/S[/math] and [math]\gamma=1/S[/math]. Because samples do not represent infinitely large communities, Simpson's index is calculated as
[math]\gamma \, = \sum_{i=1}^S \Large\frac{n_i (n_i -1)}{N (N-1)}\normalsize .[/math]
The Gini-Simpson index, which increases as the species richness in a sample increases, is given by
[math]\gamma_{GS}\, = 1 - \gamma . [/math]
Pielou index
Another evenness index was proposed by Pielou (1966[14]). The Pielou index [math]J'[/math] is defined as
[math]J' \, = \, H' / \ln(S) . \qquad (7)[/math]
If all species are represented in equal numbers in the sample, then [math]J'=1[/math]. If one species strongly dominates [math]J'[/math] is close to zero. The Pielou index is closely related to the Shannon entropy but does not depend on the number of species in the sample.
Hill numbers
The Hill numbers[15] combine species richness and evenness. The Hill diversity index of order [math]q[/math] is defined as:
[math]{^q}D = (\sum_{i=1}^S p_i \, p_i^{(q-1)})^{-\large\frac{1}{q-1}} = (\sum_{i=1}^S p_i^q)^{\large\frac{1}{1-q}} , \qquad (8)[/math]
where [math]p_i[/math] = the proportional abundance of species [math]i[/math] in the assemblage and [math]q[/math] = the order in which the index depends on rare species.
Hill's diversity numbers encapsulate species richness and variants of the Shannon and Simpson indices. They are estimated by computing the inverse of the [math](q-1)[/math]-weighted mean of the observed proportional abundances. For large positive values of [math]q[/math], the Hill numbers probe mainly the most abundant species, whereas for negative values the rarest species are emphasized (which are usually singletons, [math]p_i \sim 1/N[/math]). Negative values of [math]q[/math] are seldom included in diversity studies. For large negative values of [math]q[/math], the Hill number approaches the total number of species [math]N[/math], which is not a very useful result. Furthermore, increasing the weight given to the rarest species makes the mean proportional species abundance highly dependent on the total size of the dataset[16].
Specific Hill numbers are
[math]{^0}D = \, S ,[/math]
[math]{^1}D= \exp{H'} \quad[/math] (the limit of [math]^qD[/math] for [math]q \to 1[/math] corresponds to the exponential of the Shannon-Wiener diversity index, see #Appendix Hill number of order 1),
[math]{^2}D =\Large\frac{1}{\gamma}\normalsize \quad[/math] (the reciprocal of Simpson’s [math]\gamma\, [/math]) .
If all species are represented in equal numbers in the sample, then [math]{^0}D = {^1}D = {^2}D = S[/math]. The Hill number [math]{^q}D[/math] is also called 'biodiversity of order [math]q[/math]'. Hill numbers satisfy the so-called 'doubling property': If two completely distinct assemblages have identical Hill numbers [math]{^q}D=A[/math], then the combination of the two assemblages with equal weights has Hill number [math]{^q}D=2A[/math].[5]
An evenness index [math]E[/math] can be defined as the ratio of diversity and richness, [math]E = {^q}D / {^0}D[/math]. [16]
Taxonomic indices
If two data-sets have identical numbers of species and equivalent patterns of species abundance, but differ in the diversity of taxa to which the species belong, it seems intuitively appropriate that the most taxonomically varied data-set is the more diverse. As long as the phylogeny of the data-set of interest is reasonably well resolved, measures of taxonomic diversity are possible.
Clarke and Warwick’s taxonomic distinctness index[17] describes the average taxonomic distance – simply the “path length” between two randomly chosen organisms through the phylogeny of all the species in a data-set. The index has different forms: taxonomic diversity and taxonomic distinctness.
- Taxonomic diversity ([math]\Delta[/math]) reflects the average taxonomic distance between any two organisms, chosen at random from a sample. The distance can be seen as the length of the path connecting these two organisms through a phylogenetic tree (also called dendrogram) or a Linnean classification[17]. This index includes aspects of taxonomic relatedness and evenness,
[math]\Delta = \Large\frac{ \sum\sum_{i\lt j} \, \omega_{ij} \, n_i n_j}{N(N-1)/2}\normalsize , \qquad (9)[/math]
where [math]n_i=N p_i[/math] denotes the abundance of the [math]i[/math]-th species in the sample ([math]\sum_{i=1}^S n_i =N[/math] = the total number of individuals in the sample) and [math]\omega_{ij}[/math] is the 'distinctness weight' given to the path length (usually the number of steps in the dendrogram) linking species [math]i[/math] and [math]j[/math] in the hierarchical classification. Summations over [math]i, j[/math] are from 1 to [math]S[/math] with [math]i\lt j[/math] because the path length for two individuals of the same species is zero.
- Taxonomic distinctness ([math]\Delta^*[/math]) is the average path length between two randomly chosen but taxonomically different organisms. This index is measure of pure taxonomic relatedness,
[math]\Delta^* = \Large\frac{ \sum\sum_{i\lt j} \, \omega_{ij} n_i n_j}{\sum\sum_{i\lt j} \, n_i n_j}\normalsize . \qquad (10)[/math]
- When only presence/absence data is considered, both [math]\Delta[/math] and [math]\Delta^*[/math] converge to the same statistic [math]\Delta^+[/math], which can be seen as the average taxonomic path length between any two randomly chosen species[18],
[math]\Delta^+= \Large\frac{\sum\sum_{i\lt j} \, \omega_{ij}}{S(S-1)/2} \normalsize . \qquad (11)[/math]
Functional diversity
Functional diversity is concerned with the roles that species exert in a community. Functional diversity (presence of diverse functional groups) is a better indicator of ecosystem resilience than biodiversity (based on species richness and abundances), although a positive correlation generally exists[19]. This can be attributed to the greater number of functional groups found in richer assemblages (see also Resilience and resistance). Functional diversity increases the overall productivity of an ecosystem by allowing for more complementary functions and effective niche occupation[20], see Functional diversity in marine ecosystems.
Petchey and Gaston [21] proposed a method for quantifying functional diversity. It is based on total branch length of a dendrogram, which is constructed from species trait values. One important consideration is that only those traits linked to ecosystem functioning are used. Thus a study focusing on bird-mediated seed dispersal would exclude traits such as plumage color that are not related to this function, but traits such as beak size and shape should be included. With standard clustering algorithms a dendrogram is then constructed. For example, a community with five species with different traits will have a higher functional diversity than a community of equal richness but where the species are functionally similar. See also the article Functional diversity in marine ecosystems.
Species-abundance representations[22]
Nearly all diversity and evenness indices are based on the relative abundance of species, thus on estimates of [math]p_i[/math] in which [math]p_i = n_i / N [/math], with [math]n_i[/math] the abundance of the [math]i[/math]-th species in the sample and [math]N = \sum _{i = 1}^S \, n_i[/math] with [math]S[/math] the total number of species in the sample.
When recording the abundance of different species in a sample, it is invariably found that some species are rare, whereas others are more abundant. This feature of ecological communities is found independently of the taxonomic group or the area investigated. An important goal of ecology is to describe these consistent patterns in different communities, and explain them in terms of interactions with the biotic and abiotic environment.
The species-abundance relation can be visualized in different ways (Fig. 2).
- The rank-abundance plot is one of the best known and most informative method. In this plot species are ranked in sequence from most to least abundant along the horizontal (or [math]x[/math]) axis. Their abundances are typically displayed in a log10 format on the [math]y[/math] axis, so that species whose abundances span several orders of magnitude can be easily accommodated on the same graph. In addition, proportional and or percentage abundances are often used.
- The [math]k[/math]-dominance plot shows the cumulative percentage (the percentage of the [math]k[/math]-th most dominant plus all more dominant species) in relation to species ([math]k[/math]) rank or log species ([math]k[/math]) rank. A [math]k[/math]-dominance plot can be established for abundance (the percentage of the [math]k[/math]-th most abundant plus all more abundant species) or for biomass (the percentage of the [math]k[/math]-th highest species biomass plus percentage of all species with higher total biomass).
- The Lorenzen curve is based on the [math]k[/math]-dominance plot but the species rank [math]k[/math] is transformed to [math] (k/S) \times 100[/math] to facilitate comparison between communities with different numbers of species.
- The collector’s curve addresses a different problem. When the sampling effort is increased, and thus the number of individuals [math]N[/math] caught, new species will appear in the collection. A collector’s curve expresses the number of species as a function of the number of specimens caught. As more specimens are caught, a collector’s curve can reach an asymptotic value. However, this hardly does occur in practice due to the vague boundaries of ecological communities: as the sampling effort increases, the number of different niches increases as well.
- The species-abundance plot displays the number of species that are represented by [math]1,2, … , n [/math] individuals against the corresponding abundance. This plot can only be drawn if the collection is large and contains many species. The species are generally grouped in logarithmic density classes.
Species-abundance models[4]
Species-abundance distributions (SADs) describe the distribution of population densities of all the species in a community. They are intermediate-complexity descriptors of a community's diversity: more informative than species richness but less detailed than a list of species and their abundances. The universally observed pattern is that most species in a community are rare, while a few are common, with abundances spanning orders of magnitude[23]. The most abundant species are generally considered core species, while rare species are occasional visitors from different adjacent habitats. The universal pattern of SADs suggests that general ecological principles must govern species abundance. Different models have been proposed based on various assumptions regarding the underlying ecological principles. A few SADs that correspond to distributions commonly observed in ecosystems are presented below.
The log-series distribution
The log-series index [math]\alpha\,[/math] is a parameter of the log-series model that was derived by Fisher et al (1943[24]) from statistical arguments for very heterogeneous communities. The parameter [math]\alpha\,[/math] is a characteristic of the community and independent of sample size. It describes the way in which the individuals are divided among the species, which is a measure of diversity. The attractive properties of this diversity index are: it provides a good discrimination between sites, it is not very sensitive to density fluctuations and it is normally distributed such that confidence limits can be attached to [math]\alpha\,[/math]. Several different assumptions regarding biological dynamics can result in a log-series species-abundance distribution. The log-series model is most successful in describing succession communities with a small number of species, or communities in very harsh environments. The model is less adequate for larger areas, higher diversity or higher number of individuals[25]. There is also evidence that disturbed communities tend to follow distributions close to the log-series[26].
The log-series takes the parametric form:
[math]\alpha\,x \, , \quad \Large\frac{\alpha\, x^2}{2} \, , \frac{\alpha\, x^3}{3} , \, …..\, , \frac{\alpha\, x^{n_S}}{n_S} \qquad[/math] or [math]\qquad s(j)= \Large\frac{\alpha\, x^j}{j} \normalsize , \; j=1, …, n_S , \qquad (12)[/math]
where [math]s(j)[/math] is the number of species present with [math]j[/math] individuals in the sampled community. Since, according to the log-series model, the parameters [math]\alpha\,[/math] and [math]\,x[/math] for a particular community are assumed to be constant and [math]0 \lt \,x \lt 1[/math], the expected number of species will be the highest for the first abundance class comprising a single individual. The total number of species [math]S= \sum_{j=1}^{n_S} s(j)=\alpha \sum_{j=1}^{n_S} (x^j / j) [/math] for a large sample with many species can be approximated by
[math]S \approx \alpha \sum_{j=1}^{\infty} x^j / j = - \alpha \, \ln(1-x) . \qquad (13)[/math]
The total number of individuals [math] N \ = \sum_{j=1}^{n_S} j s(j) = \alpha \sum_{j=1}^{n_S} x^j [/math] can be approximated by (under the condition [math]x^{n_S} \lt \lt 1[/math])
[math] N \approx \alpha \sum_{j=1}^{\infty} x^j = \alpha \, x / (1-x). \qquad (14)[/math]
The values of [math]\,x[/math] and [math]\alpha[/math] can be estimated from these two equations by counting the total numbers [math]N[/math] and [math]S[/math] in the sample. It should be noted that, unless the number of species increases linearly with the sample size, the parameter [math]x[/math] depends on the sample size. The distribution over species thus changes with sample size.
The value of [math]x[/math] is usually very close to 1, such that [math]n_S \, (1-x) \lt \lt 1[/math]. In this case [math]\alpha[/math] is related to the Shannon-Wiener index and the Hill number of order 1 by [math]\alpha \approx \exp(H') = {^1}D[/math], see #Appendix Logseries rank-abundance.
The log-normal distribution
Preston (1948[27]) first suggested to use a log-normal distribution for the description of species-abundances distributions. This is a normal (Gaussian) distribution for the parameter [math]y=\ln(n)[/math], the logarithm of the species abundance [math]n[/math] (= the number of individuals belonging to a particular species). It derives from the central limit theorem, in which a large number of biotic and abiotic factors affecting population sizes act in concert to generate a lognormal distribution of abundances. Samples are considered with a large number of species and a large number of individuals. The log-normal distribution allows variation of [math]n[/math] from 0 to infinity; the corresponding values of [math]y[/math] are in the range [math][-\infty, +\infty][/math]. The distribution specifies the number of species [math]s(y)dy[/math] that may be expected with abundances [math]n[/math] in the interval [math][y,y+dy][/math]; it is given by
[math]s(y)dy = \Large\frac{S}{\sigma \sqrt{2\pi}}\normalsize \, \exp(-\Large\frac{(y-\mu)^2}{2 \sigma^2}\normalsize) \, dy , \qquad (15)[/math]
where [math]S[/math] is the total number of species and where [math]\mu[/math] and [math]\sigma[/math] are related to the average number of individuals per species and to the variance,
[math]\overline{n} = \Large\frac{N}{S}\normalsize = \exp(\mu + ½ \sigma^2) , \qquad \overline{(n-\overline{n})^2} = (\exp(\sigma^2) – 1)\, \exp(2 \mu +\sigma^2) . \qquad (16)[/math]
Contrary to the log-series distribution (Eq. 12), the log-normal distribution does not assume that species with the lowest abundance are most numerous. The log-normal distribution appears to be most appropriate for describing stable many-species communities, or sets of rapidly reproducing opportunist species. The variance [math]\sigma^2[/math] is related to the spreading of relative abundances among species: a large variance indicates uneven spreading thus low diversity and vice versa[26]. The variance also reflects ecosystem disturbance and pollution[28].
Magurran and Henderson (2003[29]) explain the difference between the log-series distribution and the log-normal distribution as follows, based on a long-term (21-year) data set, from an estuarine fish community: "The ecological community can be separated into two components. Core species, which are persistent, abundant and biologically associated with estuarine habitats, are log normally distributed. Occasional species that occur infrequently in the record, are typically low in abundance and have different habitat requirements; they follow a log-series distribution. These distributions are overlaid, producing the negative skew that characterizes real data sets." This is illustrated in Fig. 3.
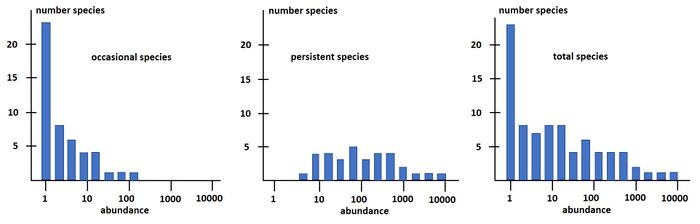
The species-abundance distribution Eq. (15) can also be written as a rank-abundance distribution:
[math]n_i = \Large\frac{N}{S}\normalsize \exp(- \sigma^2/2 + \sqrt{2} \sigma erf^{(-1)}(1-2i/S )) , \qquad (17) [/math]
where [math]n_i[/math] is the abundance of species [math]i[/math] (species ranked in order of decreasing abundance) and where [math] erf^{(-1)}[/math] is the inverse error function, [math]erf^{(-1)}(erf(x))=x, \quad erf(x)=\Large\frac{2}{\sqrt{\pi}}\normalsize \int_0^x e^{-y^2}.[/math]
The Shannon-Wiener and Hill indices for the log-normal distribution (Eq. 17) are given by
[math]H' \approx \ln(S) - \Large\frac{\sigma^2}{2}\normalsize \, , \quad {^1}D \approx S \, e^{- \large\frac{\sigma^2}{2}\normalsize }. [/math]
The biodiversity index increases (i.e. the biodiversity increases) with increasing number of species [math]S[/math]. The index also increases when [math]\sigma[/math] decreases; when all species have similar abundance (high evenness = small [math]\sigma[/math]), the biodiversity is high.
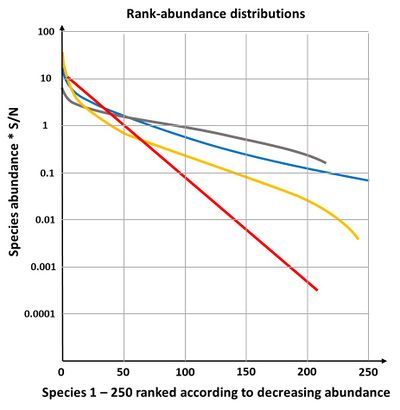
The niche preemption model or the geometric model
This model assumes that a species preempts a fraction [math]k[/math] of a limiting resource, a second species the same fraction [math]k[/math] of the remainder and so on. If the abundances are proportional to their share of the resource, the rank-abundance distribution is given by geometric series (see #Appendix Geometric model):
[math]\Large\frac{n_i}{N}\normalsize=\Large\frac{k(1-k)^{(i-1)}}{1-(1-k)^S}\normalsize , \qquad (18)[/math]
where [math]S[/math] is the number of the species in the community. For large values of [math]S[/math] this distribution depends only on the parameter [math]k[/math]. In this case the Shannon-Wiener index is given by [math]H' \approx -((1-k)/k) \ln(1-k) -\ln(k)[/math]. For small values of [math]k[/math] the index is large (high biodiversity) and for values of [math]k[/math] close to 1 the index is close to zero (low biodiversity).
The geometric model gives a straight line on a plot of log abundance against rank (species sequence), see Fig. 4. It is not very often found in nature, only in early successional stages or in species poor environments[22]. If the fraction [math]k[/math] is allowed to vary randomly, the geometric model becomes equivalent to the log-series model of species abundance.
The broken-stick model
In this model a limiting resource is compared with a stick, broken in [math]S[/math] parts at [math]S-1[/math] randomly located points. The length of the parts is taken as representative for the density of the [math]S[/math] species subdividing the limiting resource. If the species are ranked according to abundance, the expected abundance [math]n_i[/math] of species [math]i[/math] is given by[30]:
[math]\Large\frac{n_i}{N}\normalsize= \Large\frac{1}{S}\normalsize \sum_{j = i}^S \frac{1}{j} . \qquad (19)[/math]
This distribution satisfies the condition [math]N = \sum_{i=1}^S n_i [/math]. The dependence on the single parameter [math]S[/math] is weak for large values of [math]S[/math]. For large values of [math]S[/math] the Shannon-Wiener index is close to [math]H' \approx \ln(S)[/math].
The broken stick-model is most applicable to communities of species with similar competitive ability, occupying the total niche and jostling each other to determine niche boundaries. The communities have reached an equilibrium state and are small; they consist of taxonomically closely related species[6]. The broken stick distribution is not often found in nature; it describes a fairly even distribution of individuals over species (Fig. 4), which is rare in natural communities[22].
Sampling issues of species-abundance distributions
Species-abundance distributions (SADs) provide more information on ecological community characteristics than simple diversity indices for comparing communities[26]. However, for the interpretation of observed species abundance distributions, it is important that every individual of a given species is equally likely to be observed when the community is sampled, that observing each individual is an independent event, and the population remains unchanged during sampling. The scale and resolution of the sampling must be appropriate to the purpose of the study, and relevant abiotic factors must be included in the survey[31]. For example, increasing a sample to include a broader range of taxa may result in a multimodal SAD, which combines several unimodal SADs, each with its own set of parameters[25].
In the case of a statistical random distribution of a species with an expected abundance of [math]n[/math] individuals in the sampled area, the probability to find an abundance [math]m \ne n[/math] for this species is given by the Poisson distribution [math]P_n(m)=\exp(-n) \, n^m \, / (m! P_{n,N})[/math]. [math]P_{n,N}[/math] is a normalization factor to ensure that [math]\sum_{m=1}^N P_n(m)=1[/math]. If [math]s(n)dn/S[/math] is interpreted as the expected probability to find a species with abundance in the range [math] [n- ½dn, n+ ½dn] [/math] in large samples, then in small samples one will find the species-abundance distribution [math]\hat s(n)=\sum_{m=1}^N P_n(m) s(m)[/math] instead of the expected distribution [math]s(n)[/math]. If the abundance [math]n[/math] is large, the Poisson distribution is strongly peaked around [math]m=n[/math], which implies [math]\hat s(n) \approx s(n) [/math]. The species-abundance distributions determined from 'small' samples (abundances [math]n[/math] substantially less than 100) are generally biased.
In practice, the spatial distribution of species is often not uniform. In this case, even large samples can produce biased results. Clustered spatial distributions lead to the greatest bias.
Rarefaction
Comparing diversity indices determined from different field surveys is generally difficult. As noted before, the number of species (species richness [math]S[/math]) found in a sample strongly depends on the sampling technique and on the sample size, i.e. on the number of individuals [math]N[/math] in the sample. Under certain conditions it is possible to take into account the influence of the sample size on the species richness [math]S[/math]. One condition is that the same sampling technique is used. Another condition is that the spatial distribution of individuals and species in the assemblage from which the sample is taken is random. If these conditions are met, the richness [math]Sm[/math] of a sample with [math]M[/math] individuals and the richness [math]Sn[/math] of a larger sample with [math]N[/math] individuals and abundances [math]n_1, n_2, …., n_{Sn}[/math] are statistically related by the formula (see #Appendix Rarefaction)
[math]Sm = \sum_{i=1}^{Sn} \Big( 1 - \large\frac{(N-M)!}{N!}\frac{(N-n_i)!}{(N-n_i-M)!}\normalsize \Big) . \qquad (20)[/math]
This so-called 'rarefaction' formula allows different samples to be rescaled to the same size. However, the rarefaction formula cannot be applied for assemblages with many rare species because the spatial distribution is not sufficiently random.
Ecosystem health assessment
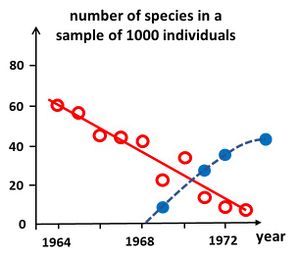
Simple diversity indices enable relatively quick assessments of ecosystem health and timely management interventions to mitigate the effects of disturbance. Analysis of these indices over time provides managers with early warning signals of the effects of disturbance on ecological communities. Several methods have been developed to enable a rapid assessment of ecosystem health.
Degradation of ecosystem health can be signaled by the time evolution of species richness (number of species [math]S[/math]). For comparing the richness figures of samples taken at different times, the samples must be rescaled to the same number of species[32]. An example of such a rescaled time series using the rarefaction formula (20) is shown in Fig. 5. A decrease of the number of species signals ecosystem degradation, whereas an increase signals recovery. However, the cause of degradation is not revealed by this method, and requires additional investigation.
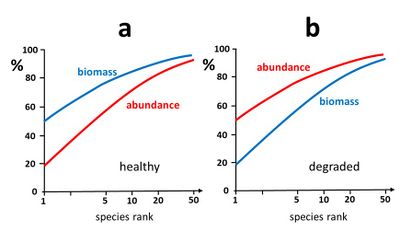
Another method consists of establishing species-abundance-biomass curves[3]. These curves provide information on the temporal evolution (or spatial distribution) of the trophic ecosystem structure. It is generally observed that an ecosystem in good health is characterized by a trophic structure where at the highest trophic levels relatively few species with relatively low abundance (e.g. relatively small populations of relatively large predators) represent a large part of the total biomass. In a [math]k[/math]-dominance plot for both abundance and biomass, the biomass curve is therefore typically higher than the abundance curve[33], see Fig. 6a. In contrast, when the ecosystem is stressed and degraded, the highest trophic levels are generally most affected (e.g. through bio-accumulation of pollutants, habitat disturbance, loss of suitable prey) leading to uncontrolled growth of species at lower trophic levels (including fast growing populations of opportunistic non-selective stress-resistant species). In this case, a [math]k[/math]-dominance plot for both abundance and biomass typically exhibits a biomass curve lower than the abundance curve, see Fig. 6b.
The analysis of the [math]k[/math]-dominance plots can be summarized in a single parameter, the Shannon-Wiener evenness proportion ([math]SEP[/math]) defined as the ratio of biomass and abundance evenness (Eq. 7)[34]:
[math]SEP = J'_{biomass}/J'_{abundance}=H'_{biomass}/H'_{abundance} . \qquad (21)[/math]
A healthy ecosystem with few high-trophic individuals representing a high percentage of the biomass has a biomass distribution with lower evenness than the abundance distribution and thus a low value of [math]SEP[/math]. Such a system can turn under stress (habitat destruction, pollution) into a degraded, less complex ecosystem with a few highly abundant low-trophic species, and a biomass distribution with greater evenness than the abundance distribution, corresponding to a high value of [math]SEP[/math].
Ecosystem recovery from a highly stressed situation (high [math]SEP[/math]) passes through a so-called ecotone point of maximum biodiversity (maximum [math]H'_{abundance}[/math]). At the ecotone point the abundance of original species is increasing while a substantial population of opportunistic species is still present[3].
In order to avoid problems with single-species samples ([math]H'_{abundance}=0[/math]), a related index called [math]ISEP[/math] was defined as[35]
[math]ISEP = \log_{10}(1+1/SEP) . \qquad (22)[/math]
With this index, ecosystem degradation is signaled by a decrease of [math]ISEP[/math]. The consistency and usefulness of the [math]ISEP[/math] index was confirmed in a large field survey program in the Korean coastal waters, where the presence of stress indicators (particulate organic carbon, particulate nitrogen, turbidity) was negatively correlated with [math]ISEP[/math][36].
Criticism of biodiversity indices
The characterization of ecosystems by one or a few numbers is an extreme simplification of their real complexity. An often voiced criticism is therefore that ecosystem management cannot be guided by biodiversity indices alone[37]. Biodiversity indices are proxies of biodiversity. There is no single 'right' indicator[38]. Biodiversity indices embody certain aspects of ecosystems, but are insensitive to many others. The interpretation of biodiversity indices as a characteristic of ecosystems is therefore problematic. An unequivocal relationship with environmental conditions is often lacking. The interpretation of results can be profoundly altered depending on the choice of the biodiversity index[39]. Biodiversity indices are therefore considered too abstract and unsuitable for public and political communication.
Biodiversity indices depend on the way they are determined. Since the statistical distribution of samples is generally not known, it is difficult to estimate the accuracy of a given index value[40]. As discussed earlier, the sample size and the thoroughness of the sampling play an important role[32]. The sampling of species with a patchy distribution pattern easily leads to flawed (underestimated or overestimated) numbers. Tiny species and rare species with an important ecosystem role are often not fully included or even completely missed. Another issue is related to defining the spatial boundaries of an ecosystem. It can be argued that a natural community is an open system with nothing approaching a fixed number of species[11].
A more fundamental critics relates to the premise of most biodiversity indices that all species are equal (this critics holds to a lesser extent for functional diversity indices). The identity of species and their role in the community is lost in the biodiversity indices[40]. Often a few particular species can have an impact on the community or ecosystem that far exceeds their relative abundance or biomass. Such keystone species can fulfill different roles in ecosystem functioning, for example:
- Controlling the abundance of species at lower trophic levels (e.g. apex predators, see Trophic cascade)
- Creating microhabitats for other species by activities such as burrowing, scraping, sediment retention, sheltering, shading, … (eco-engineer function)
- Transforming chemicals into compounds that can be assimilated by other species (e.g. nitrogen fixation)
- Rare species that form a reservoir of functional and genetic diversity, contributing to the stability and resilience of the ecosystem
An assessment of ecosystem health or resilience cannot be based on biodiversity indices alone, but has to consider the specific role of keystone species[41].
Despite the above criticisms, biodiversity indices, and in particular the analysis of species abundance distributions, have proven useful in practice to act as an early warning tool for the effects of disturbance on ecological communities, and to provide a means for measuring the implementation of regulations for ecological management[26].
Appendix Completeness
It is assumed that individuals and species are randomly distributed in the sample and that the total number [math]N[/math] of individuals is large. An estimate of the probability that species [math]i[/math] is not found after [math]N[/math] independent draws from the sample is given by [math]q_i=(1-p_i)^N[/math]. The probability [math]p_i[/math] of finding species [math]i[/math] can be estimated with [math]p_i=n_i/N[/math]. An estimate of the probability that not all species are found after [math]N[/math] independent draws is given by [math]C'= \sum_{i=1}^S p_i \, q_i[/math]. The probability that all species are found after [math]N[/math] independent draws is given by [math]C=1-C'[/math], which is Eq. (2).
Appendix Shannon-Wiener index
The Shannon-Wiener diversity index is a measure of the information (in fact, the 'lack of information', or 'uncertainty' or 'information entropy') represented by a sample, where information is defined as the minimum length of a string of digits necessary to describe the sample. The minimum length of a string of (binary) digits to describe a number is proportional to the logarithm of this number. All the different ways in which [math]N[/math] individuals can be distributed in numbers [math]n_1, n_2, …, n_S[/math] for the species [math]1, 2, …., S[/math] are equivalent and thus provide no additional information about the sample. With this definition, a measure of the information entropy in a large sample is given by the logarithm of the number [math]P[/math] of all different permutations of individuals that give the same distribution of individuals over species. If [math]P[/math] is large, the sample can be ordered in many distinct equivalent ways and thus has a low information content (= high information entropy = high diversity). This is the case, for example, if all [math]N[/math] individuals in a sample belong to different species. The number of equivalent distinct permutations is then equal to [math]P=N![/math] (the first individual in an ordered sample can be chosen in [math]N[/math] ways, the second in [math]N-1[/math] ways and so on). If all the individuals belong to the same species there are no distinct equivalent permutations, i.e. [math]P=1[/math]. If there are [math]n_1[/math] individuals of species 1, [math]n_2[/math] individuals of species 2, and so on, then the number of equivalent distinct permutations is [math]P = N!/(n_1! \times n_2! \times . . . . \times n_S!)[/math]. Taking the natural logarithm gives [math]N \times[/math] the Brillouin index [math]H[/math]. Assuming that the numbers [math]N, n_1, n_2, ….[/math] are very large, one can approximate [math]\ln(n_i!) \approx n_i\, \ln(n_i) [/math]. This gives [math]\ln(P) \approx N \, \ln(N) - n_1 \, \ln(n_1) - n_2\, \ln(n_2) - …..- n_S \, \ln(n_S) [/math]. For large representative samples the probability of occurrence of species [math]i[/math] is given by [math]p_i=n_i/N[/math]. We further have [math]\sum_{i=1}^{S} p_i=1[/math]. Substitution gives [math]\ln(P) \approx -N \sum_{i=1}^{S} p_i \, \ln(p_i)[/math], which is [math]N \times[/math] the Shannon-Wiener index [math]H'[/math]. Division by [math]N[/math] makes the index independent of the sample size.
Another interpretation of the Shannon-Wiener index is: the mean number of digits required for describing the probability [math]p_i[/math] to find [math]n_i[/math] individuals of species [math]i[/math] in the sample of [math]N[/math] individuals. The number of digits for describing the probability [math]p_i[/math] is proportional to [math]-\ln(p_i)[/math] (the rarer the species, the smaller [math]p_i[/math] and the more digits are needed). The mean is obtained by taking the weighted sum of the number of digits: [math]H'= - \sum_{i=1}^S p_i \ln(p_i)[/math].
Appendix Hill number of order 1
Take [math]q=1+\epsilon[/math] and [math]\epsilon \to 0[/math], then [math]p_i^q \to p_i+\epsilon \large\frac{d}{d \epsilon} p_i^{1+\epsilon}\normalsize \approx p_i + \epsilon p_i \ln p_i[/math]. Because [math]\sum_{i=1}^S p_i = 1[/math], we have
[math]^1D = \lim_{\epsilon \to 0} (1 + \epsilon \sum_{i=1}^S p_i \ln p_i)^{-1/\epsilon} = \exp(-\sum_{i=1}^S p_i \ln p_i)[/math].
Appendix Logseries rank-abundance
The conversion of the species-abundance distribution Eq. (12) into the rank-abundance distribution gives [math](n_i, x_i), \; i=1, …., n_S[/math], with [math]n_i=n_S+1-i, \quad x_i=\alpha \sum_{j=n_S+1-i}^{n_S} (x^j/j)[/math]. Summation over all species gives [math]N=\sum_{i=1}^{n_S} n_i \Delta x_i[/math], with [math]\Delta x_i=x_i-x_{i-1}=\alpha x^j/j, \; j=n_S+1-i, \; x_0=0[/math].
The Shannon-Wiener index is given by [math]H'=- \sum_{i=1}^{n_S} \Delta x_i (n_i/N) \ln(n_i/N)=\ln(N)-(\alpha/N)\sum_{j=1}^{n_S} x^j \ln(j)[/math]. Assuming [math]n_S\gt \gt 1[/math] and [math]n_S (1-x) \lt \lt 1[/math] we have [math]\alpha n_S \approx N[/math] and [math]\sum_{j=1}^{n_S} x^j \ln(j) \approx \sum_{j=1}^{n_S} \ln(j) = \ln(n_S!) \approx n_S \ln(n_S) \approx (N/ \alpha)(\ln(N)-\ln(\alpha))[/math]. Substitution yields [math]H' \approx \ln(\alpha)[/math].
Appendix Geometric model
According to the assumptions underlying the model, the numbers [math]\, n_1, n_2, …., n_S \, [/math] of species [math]\, 1, 2, …., S \,[/math] are
[math]n_1=c \, k, \; n_2= c \, k(1-k), \; n_3=c \, k(1-k-k(1-k))= c \, k(1-k)^2, …., \; n_S= c \, k(1-k)^{(S-1)} [/math].
We have [math]N = \sum_{i=1}^S n_i = c \, k \sum_{i=1}^S (1-k)^{(i-1)} = c \, (1-(1-k)^S) [/math], hence [math]c=\Large\frac{N}{1-(1-k)^S}[/math].
Appendix Rarefaction
Consider an assemblage consisting of [math]N[/math] individuals belonging to [math]Sn[/math] species with abundances [math]n_1, n_2, …, n_{Sn}[/math], which are randomly distributed over [math]N[/math] locations [math]x_1, x_2, …., x_N[/math]. The possible number of differently distributed similar assemblages equals [math]N![/math]. Now consider a sample taken from this assemblage containing [math]M[/math] individuals at arbitrary locations [math]x_1, x_2, …, x_M[/math]. The number of possible different sample choices equals [math]\mathcal{N}=N!/[M!(N-M)!][/math]. The number of possible different sample choices from which species [math]i[/math] is excluded equals [math]\mathcal{N_i}=(M-n_i)!/[M! (N-n_i-M)!][/math]. The probability that among all different random sample choices the chosen sample does not contain species [math]i[/math] is given by [math]\mathcal{P_i}=\mathcal{N_i}/\mathcal{N}[/math]. Therefore, [math]Sm = \sum_{i=1}^{Sn} \Big( 1 - \mathcal{P_i} \Big)[/math] is the sum of the probabilities that either species [math]1[/math], or species [math]2[/math], or …., or species [math]Sn[/math] is included in a random sample of [math]M\lt N[/math] individuals. The sum of these probabilities gives the most probable value of the number [math]Sm[/math] of different species in a sample of [math]M[/math] individuals taken randomly from the larger assemblage of [math]N[/math] individuals (Eq. 20).
List of symbols
| Symbol | Description | Symbol | Description | Symbol | Description |
|---|---|---|---|---|---|
| [math]D[/math] | diversity index | [math]H'[/math] | Shannon-Wiener index (entropy) | [math]i , j[/math] | referring to species [math]i[/math] , species [math]j[/math] |
| [math]n_i[/math] | number of individuals of species [math]i[/math] (=species abundance) | [math]N[/math] | total number of individuals | [math]p_i[/math] | probability of presence of species [math]i[/math] (usually estimated as relative abundance [math]n_i/N[/math]) |
| [math]q[/math] | order of Hill number | [math]S[/math] | number of species | [math]\alpha[/math] | index referring to diversity within a particular site (or habitat or community) |
| [math]\beta[/math] | index referring to change in diversity between sites | [math]\gamma[/math] | index referring to diversity within a landscape or region | [math]\omega_{i,j}[/math] | taxonomic distance between species [math]i[/math] and [math]j[/math] (path length connecting these organisms in a phylogenetic tree or dendrogram) |
Related articles
- Marine Biodiversity
- Biodiversity and Ecosystem function
- Functional diversity in marine ecosystems
- Biological Trait Analysis
- Wikipedia article Diversity index
Further reading
- Magurran, A. E. 2004. Measuring biological diversity, Blackwell Publishing: Oxford, UK. 256 p
References
- ↑ Swingland, I.R. 2013. Definition of biodiversity. In: Encyclopedia of Biodiversity, Vol. 1. Elsevier, pp. 399-410
- ↑ 2.0 2.1 Whittaker, R.H. 1972. Evolution and measurement of species diversity. Taxon 21: 213-251
- ↑ 3.0 3.1 3.2 3.3 3.4 Pearson, T.H. and Rosenberg, R. 1978. Macrobenthic succession in relation to organic enrichment and pollution of the marine environment. Oceanogr. Mar. Biol. Ann. Rev. 16: 229-311
- ↑ 4.0 4.1 Magurran, A. E. 2004. Measuring biological diversity, Blackwell Publishing: Oxford, UK. 256 p
- ↑ 5.0 5.1 Chao, A., Gotelli, N.J., Hsieh, T.C., Sander, E.L., Ma, K.H., Colwell, R.K. and Ellison, A.M. 2014. Rarefaction and extrapolation with Hill numbers: a framework for sampling and estimation in species diversity studies. Ecological Monographs 84: 45–67
- ↑ 6.0 6.1 Tokeshi, M. 1993. Species abundance patterns and community structure. Advances in Ecological Research 24: 111–186
- ↑ Clifford H.T. and Stephenson W. 1975. An introduction to numerical classification. London: Academic Express.
- ↑ Whittaker R.H. 1977. Evolution of species diversity in land communities. Evolutionary Biol. 10: 1-67
- ↑ Shannon C. E. and Weaver W. 1949. The mathematical theory of communication. Urbana, IL: University of Illinois Press.
- ↑ 10.0 10.1 Pielou E.C. 1975. Ecological diversity. New York: Wiley Interscience.
- ↑ 11.0 11.1 Peet, R.K. 1974. The measurement of species diversity. Annual Review of Ecology and Systematics 5: 285-307
- ↑ Pielou E.C. 1969. An introduction to mathematical ecology. New York: Wiley.
- ↑ Simpson E.H. 1949. Measurement of diversity. Nature 163: 688.
- ↑ Pielou, E.C. 1966. The measurement of diversity in different types of biological collection. Journal of Theoretical Biology 13: 131–144
- ↑ Hill, M.O. 1973. Diversity and evenness: a unifying notation and its consequences. Ecology 54: 427–473
- ↑ 16.0 16.1 Tuomisto, H. 2017. Defining, Measuring, and Partitioning Species Diversity. In: Reference Module in Life Sciences. ISBN 978-0-12-809633-8
- ↑ 17.0 17.1 Warwick R.M. and Clarke K.R. 2001. Practical measures of marine biodiversity based on relatedness of species. Oceanogr. Mar. Biol. Ann. Rev. 39: 207-231
- ↑ Clarke K.R. and Warwick R.M. 1998. A taxonomic distinctness index and its statistical properties Journal of Applied Ecology 35 (4): 523-531
- ↑ McCann, K. S. 2000. The diversity-stability debate. Nature 405: 228–233
- ↑ Cardinale, B. J., Wright, J. P. and Cadotte, M. W., Carroll, I.T., Hector, A., Srivastava, D.S., Loreau, M. and Weis, J.J. 2007. Impacts of plant diversity on biomass production increase through time because of species complementarity. PNAS 104: 18123–18128
- ↑ Petchey O.L. and Gaston K.J. 2002. Functional diversity (FD), species richness and community composition. Ecology letters Vol. 5 (3): 402-411
- ↑ 22.0 22.1 22.2 Heip, C.H.R., Herman, P.M.J. and Soetaert, K. 1998. Indices de diversité et régularité. [Indices of diversity and evenness]. Océanis (Doc. Océanogr.) 24(4): 67-87
- ↑ McGill, B.J., Etienne, R.S., Gray, J.S., Alonso, D., Anderson, M.J., Benecha, H.K., Dornelas, M., Enquist, B.J., Green, J.L., He, F., Hurlbert, A.H., Magurran, A.E., Marquet, P.A., Maurer, B.A., Ostling, A., Soykan, C.U., Ugland, K.I. and White, E.P. 2007. Species abundance distributions: moving beyond single prediction theories to integration within an ecological framework. Ecology Letters, 10, 995–1015
- ↑ Fisher, R. A., Corbet, A. S. and Williams, C. B. 1943. The relation between the number of species and the number of individuals in a random sample of an animal population. Journal of Animal Ecology 12: 42-58
- ↑ 25.0 25.1 Antao, L.H., Magurran, A.E. and Dornelas, M. 2021. The Shape of Species Abundance Distributions Across Spatial Scales. Front. Ecol. Evol. 9:626730
- ↑ 26.0 26.1 26.2 26.3 Matthews, T.J. and Whittaker, R.J. 2015. On the species abundance distribution in applied ecology and biodiversity management. Journal of Applied Ecology 52: 443–454
- ↑ Preston, F.W. 1948. The commonness and rarity of species. Ecology 29: 254–283
- ↑ Dornelas, M., Moonen, A.C., Magurran, A.E. and Barberi, P. 2009. Species abundance distributions reveal environmental heterogeneity in modified landscapes. Journal of Applied Ecology 46: 666–672
- ↑ 29.0 29.1 Magurran, A.E. and Henderson, P.A. 2003. Explaining the excess of rare species in natural species abundance distributions. Nature 422: 714–716
- ↑ McArthur, R.H. 1957. On the relative abundance of bird species. Proc. Natl. Acad. Sci. USA 43: 293-295
- ↑ Austin, M. 2007. Species distribution models and ecological theory: A critical assessment and some possible new approaches. Ecological modelling 200: 1-19
- ↑ 32.0 32.1 Sanders, H.L. 1968. Marine benthic diversity: A comparative study. American Naturalist 102: 243-282
- ↑ 33.0 33.1 Warwick, R. M. 1986. A new method for detecting pollution effects on marine macrobenthic communities. Marine Biology 92: 557–562
- ↑ McManus, J.W. and Pauly, D. 1990. Measuring ecological stress: Variations on a theme by R.M. Warwick. Marine Biology 106: 305–308
- ↑ Yoo, J.W., Lee, Y.W., Ruesink, J.L., Lee, C.G., Kim, C.S., Park, M.R., Yoon, K.T., Hwang, I.S., Maeng, J.H., Rosenberg, R. and Honh, J.S. 2010. Environmental quality of Korean coasts as determined by modified Shannon–Wiener evenness proportion. Environ. Monit. Assess. 170: 141–157
- ↑ Yoo, J.-W., Lee, Y.-W., Park, M.-R., Kim, C.-S., Kim, S., Lee, C.-L., Jeong, S.-Y., Lim, D. and Oh, S.-Y. 2022. Application and Validation of an Ecological Quality Index, ISEP, in the Yellow Sea. J. Mar. Sci. Eng. 10, 1908
- ↑ Karydis, M. 2022. Critique on Ecological Methodologies Used in Water Quality Studies and Coastal Management: A Review. J. Mar. Sci. Eng. 10, 701
- ↑ Bartkowski, B., Lienhoop, N. and Hansjurgens, B. 2015. Capturing the complexity of biodiversity: A critical review of economic valuation studies of biological diversity. Ecological Economics 113: 1-14
- ↑ Morris, E.K., Caruso, T., Buscot, F., Fischer, M., Hancock, C., Maier, T.S., Meiners, T., Muller, C., Obermaier, E., Prati, D., Socher, S.A., Sonnemann, I., Waschke, N., Wubet, T., Wurst, S. and Rillig, M.C. 2014. Choosing and using diversity indices: insights for ecological applications from the German Biodiversity Exploratories. Ecology and Evolution 4: 3514–3524
- ↑ 40.0 40.1 Barrantes, G. and Sandoval, L. 2009. Conceptual and statistical problems associated with the use of diversity indices in ecology. Rev. Biol. Trop. 57: 451-60
- ↑ Power, M.E., Tilman, D., Estes, J.A., Menge, B.A., Bond, W.J., Mills, L.S., Daily, G., Castilla, J.C., Lubchenco, J. and Paine, R.T. 1996. Challenges in the Quest for Keystones. BioScience 46: 609-620
Please note that others may also have edited the contents of this article.
|






