Difference between revisions of "Ekman transport"
Dronkers J (talk | contribs) (Created page with " {{Definition|title = Ekman transport|definition = Wind-driven water transport deflected by the Earth's rotation.}} ==Ekman spiral== image:Ekman spiral.JPG|right|thumb|3...") |
Dronkers J (talk | contribs) |
||
| Line 1: | Line 1: | ||
| − | |||
{{Definition|title = Ekman transport|definition = Wind-driven water transport deflected by the Earth's rotation.}} | {{Definition|title = Ekman transport|definition = Wind-driven water transport deflected by the Earth's rotation.}} | ||
| Line 93: | Line 92: | ||
<math>w_E = \Large \frac{1}{\rho f} \Big( \frac{\partial}{\partial x}\normalsize \tau_w^{(y)} - \Large\frac{\partial}{\partial y}\normalsize \tau_w^{(x)} \Big) + \Large\frac{\beta}{\rho f^2}\normalsize \tau_w^{(x)} . \qquad (13)</math> | <math>w_E = \Large \frac{1}{\rho f} \Big( \frac{\partial}{\partial x}\normalsize \tau_w^{(y)} - \Large\frac{\partial}{\partial y}\normalsize \tau_w^{(x)} \Big) + \Large\frac{\beta}{\rho f^2}\normalsize \tau_w^{(x)} . \qquad (13)</math> | ||
| − | This expression has a singularity at the equator where <math>f=0</math>, which is due to the model simplifications. The formula (13) shows that the Ekman transport mechanism can generate substantial vertical water motions near the equator. The subtropical trade winds which are oriented E-W (<math>\tau_w^{(x)} < 0</math>) increase towards the equator (<math>f^{-1} \, \partial \tau_w^{(x)} / \partial y </math> > 0). This produces downwelling currents (<math>w_E < 0</math>) in the surface Ekman layer of the subtropical ocean. The transition zones from the low-latitude trade winds to the westerlies at higher latitudes can be considered large-scale anticyclonic gyres with corresponding downwelling currents<ref name=CP/>. | + | This expression has a singularity at the equator where <math>f=0</math>, which is due to the model simplifications. The formula (13) shows that the Ekman transport mechanism can generate substantial vertical water motions near the equator. The subtropical trade winds which are oriented E-W (<math>\tau_w^{(x)} < 0</math>) increase towards the equator (<math>f^{-1} \, \partial \tau_w^{(x)} / \partial y </math> > 0). This produces downwelling currents (<math>w_E < 0</math>) in the surface Ekman layer of the subtropical ocean. The transition zones from the low-latitude trade winds to the westerlies at higher latitudes can be considered large-scale anticyclonic gyres with corresponding downwelling currents<ref name=CP/>, see [[Ocean circulation]]. |
| Line 100: | Line 99: | ||
:[[Shelf sea exchange with the ocean]] | :[[Shelf sea exchange with the ocean]] | ||
:[[Geostrophic flow]] | :[[Geostrophic flow]] | ||
| − | :[[ | + | :[[Ocean circulation]] |
Revision as of 21:20, 20 June 2024
Definition of Ekman transport:
Wind-driven water transport deflected by the Earth's rotation.
This is the common definition for Ekman transport, other definitions can be discussed in the article
|
Contents
Ekman spiral
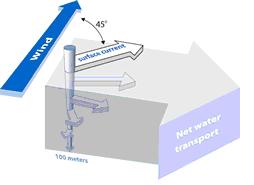
Due to the Earth’s rotation, ocean currents are deflected to the right in the Northern Hemisphere and to the left in the Southern Hemisphere. This phenomenon is called Coriolis effect and explained in the article Coriolis acceleration. This means that currents driven by wind stress at the water surface do not follow the wind direction, but are deviated. The wind-driven water transport deflected by the Earth's rotation is called Ekman transport, named after the Swedish oceanographer Vagn Walfrid Ekman who first described this phenomenon[1]. The deflection angle of the current increases with depth, measured from the surface (Fig. 1). The veering of the current with depth depends on the intensity of the turbulent fluid motions in the water column, which can be captured in a so-called 'eddy viscosity' coefficient [math]K_z[/math]. Ekman transport is largely restricted to the ocean upper layer with thickness [math]D_E[/math], the so-called Ekman depth, which is of the order of 100 m. Although the currents associated with Ekman transport are small (typically less than 0.1 m/s), the large horizontal extent makes that the total amount of water transported can be huge, comparable to the transport of major ocean currents such as the Gulf Stream or the Kuroshio[2].
When surface waters are exposed to wind stress, they drag the deeper layers with them. Each layer of water is moved by friction from the shallower layer and each deeper layer moves more slowly than the layer above it. The direction of flow in each layer is deflected by the Earth's flow rotation. The resulting veering of the current is called the Ekman spiral. The deflection of the surface current has an angle of 45° (bending to the right, in the Northern Hemisphere). At the Ekman depth, the water flows in a direction opposite to the surface current. The depth-averaged net water transport is perpendicular (90°) to the wind direction and this is the effective direction of the Ekman transport. [3] Field observations show that the veering angles of the wind-driven current are in reality larger than predicted by the Ekman theory. The surface current lies more than the predicted 45° to the right of the wind, and the current amplitude decreases at a faster rate than it turns to the right, resulting in a flatter spiral than the theory predicts. These differences are due to processes not considered in the idealized Ekman model, for example stratification[4].
Consequences of Ekman transport
Ekman transport generates vertical water motions (upwelling or downwelling) through several mechanisms. Vertical water motions are of great significance for the ocean ecosystem. In the case of upwelling, they stimulate primary production by bringing nutrient-rich water from the deep ocean to the surface. In the case of downwelling, Ekman transport can contribute to carbon sequestration by downward transport of dissolved inorganic and organic carbon into deep ocean layers[5].
Vertical water transport is generated by zonal wind stress close to the equator, resulting from the varying strength of Ekman transport with latitude and the associated convergence or divergence of ocean currents (see Appendix). Diverging Ekman transport produces upwelling, also called Ekman suction. Converging Ekman transport produces downwelling, also called Ekman pumping. The transition zones of low-latitude trade winds and mid-latitude westerlies generate large-scale anticyclonic gyres with corresponding downwelling zones in the surface Ekman layer of the subtropical oceans[2].
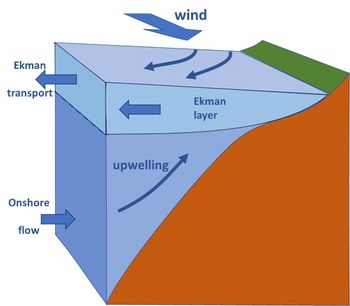
Upwelling and downwelling are particularly important at the shelf sea boundaries with the ocean. Coast-parallel winds drive surface waters offshore (if the coast is to the left, in the Northern Hemisphere) or onshore (if the coast is to the right). In the former case, the water surface dips towards the coast. The associated hydrostatic pressure gradient generates onshore transport of deep ocean water (beneath the Ekman layer) that then upwells to the surface (Figure 2). In the latter case, a rise in the water surface towards the coast generates a hydrostatic pressure gradient that causes the downward flow of shelf water that is then transported offshore to the deep ocean.
Appendix: Mathematical derivations
The ocean response to a surface wind stress [math]\vec{\tau}(z=0) = \vec{\tau}_w[/math] on a rotating Earth follows from the momentum balance equations (see Coriolis acceleration)
[math]\Large\frac{1}{\rho}\frac{\partial \tau^{(x)}}{\partial z}\normalsize = - f \, v \, \qquad (1)[/math]
[math] \Large\frac{1}{\rho}\frac{\partial \tau^{(y)}}{\partial z}\normalsize = f \, u . \qquad (2)[/math]
The Coriolis parameter [math]f[/math] is given by [math]f=2 \Omega \sin \phi[/math], where [math]\Omega \approx 7.29211^{−5} \, s^{−1}[/math] is the radial earth rotation frequency and [math]\phi[/math] the elevation radian angle indicating latitude.
Meaning of the other symbols:
[math]x, \, y\,=[/math] spatial coordinates, along the horizontal Cartesian [math]x[/math] and [math]y[/math] axes
[math]z=[/math] coordinate along the vertical axis (upwards positive, water surface at [math]z=0[/math] )
[math]u(z),\, v(z) =[/math] components of the current velocity [math]\vec{u}(z)[/math] along the [math]x[/math] and [math]y[/math] axis, respectively
[math]\rho=[/math] seawater density
[math]\tau^{(x)}(z), \, \tau^{(y)}(z) =[/math] components of the shear stress along the [math]x[/math] and [math]y[/math] axis, respectively
The equations (1) are a simplified form of the momentum balance following the assumptions of (a) steady flow (no time dependence), (b) uniform seawater density and (c) no sea surface slope (i.e. no piling up of seawater against boundaries).
We assume that the wind stress acts in the [math]x[/math] direction, [math]\tau^{(x)}(z=0) = \tau_w \, , \, \tau^{(y)}(z=0)=0[/math]. The wind shear stress is related to the wind speed [math]V[/math] (usually taken at 10 m above the water surface) and the roughness of the water surface. It can be estimated from the empirical formula [math]\tau_w = \rho_{air} C_D V^2[/math], with [math]\rho_{air} \approx 1.2 \; kg \, m^{-3}[/math] and [math]C_D \approx (1-2) \, . \, 10^{-3}[/math].
Integration of Eq. (1) over the depth gives the net mass transports [math]M^{(x)} \, , \, M^{(y)}[/math] in the [math]x[/math] and [math]y[/math] directions respectively:
[math]M^{(x)} = 0 \, , \, M^{(y)} \approx \int_{-\infty}^0 v dz = - \Large\frac{\tau_w}{\rho f}\normalsize. \qquad (3)[/math]
This expression shows that wind stress along the [math]x[/math] direction produces a net mass transport, the so-called Ekman transport, in the [math]y[/math] direction. It should be noted that Ekman transport does not depend on the rate of momentum diffusion in the vertical or on effects of stratification.
We will adopt a further simplification by assuming that shear stresses are related to the local velocity gradient and a constant eddy viscosity [math]K_z[/math] (typically in the range 0.01-0.05 m2/s),
[math]\vec{\tau}(z) = \rho \, K_z \, \Large\frac{\partial \vec{u}}{\partial z} \normalsize . \qquad (4)[/math]
The momentum balance equations (1) then become
[math] K_z \Large\frac{\partial^2 u}{\partial z^2}\normalsize = - f \, v \, , \quad K_z \Large\frac{\partial^2 v}{\partial z^2}\normalsize = f \, u . \qquad (5)[/math]
With the assumption of great depth, the solution of these linear equations take the form
[math]u(z) = \Re [a \exp(\kappa z)] \, , \; v(z) = \Re [b \exp(\kappa z)] , \quad \Re[\kappa] \gt 0 , \qquad (6)[/math]
where [math]a, b, \kappa[/math] are complex numbers. Solving [math]\kappa[/math] by substitution of Eq. (6) in Eq. (5) gives
[math]a = \pm i b \, , \quad \kappa = \Large\frac{\pi \pm i \pi}{D_E}\normalsize , \qquad (7)[/math]
where [math]D_E[/math] is the Ekman depth given by [math]\; D_E = \pi \sqrt{\large\frac{2 K_z}{|f|}\normalsize} . \qquad (8)[/math]
The shear stress near the water surface [math]\rho K_z \Large\frac{d \vec{u}}{dz}\normalsize (z=0)[/math] is equal to the wind stress [math]\vec{\tau}_w[/math] along the [math]x[/math] axis. This condition yields
[math]a = u_0 e^{-i \pi /4} \, , \quad u_0 = \Large\frac{\sqrt{2} \pi \tau_w}{\rho |f| D_E}\normalsize \qquad (9)[/math]
and in the Northern Hemisphere,
[math]u(z) = u_0 \cos \Big(-\large\frac{\pi}{4}\normalsize + \large\frac{\pi z}{D_E}\normalsize \Big) \exp\Big(\large\frac{\pi z}{D_E}\normalsize\Big) \, , \; v(z) = u_0 \sin \Big(-\large\frac{\pi}{4}\normalsize + \large\frac{\pi z}{D_E}\normalsize \Big) \exp\Big(\large\frac{\pi z}{D_E}\normalsize\Big) . \qquad (10)[/math]
This expression represents the Ekman spiral shown in Fig. 1.
Ekman transport generates a vertical velocity [math]w(z)[/math] through the continuity equation
[math]\Large\frac{\partial w}{\partial z}\normalsize = - \Big( \Large\frac{\partial u}{\partial x}\normalsize + \Large\frac{\partial v}{\partial y}\normalsize \Big) . \qquad (11)[/math]
We assume that the [math]x[/math] axis is oriented W-E and the [math]y[/math] axis S-N. In this case [math]df/dx= 0[/math] and [math]df/dy = \beta, \; \beta = 2 \Omega \cos \phi /R[/math], where [math]R[/math] is the Earth's radius.
Now we derive Eq. (2) with respect to [math]x[/math] and Eq. (1) with respect to [math]y[/math] and subtract the results. This yields
[math] \Large\frac{1}{\rho}\frac{\partial}{\partial z} \Big( \frac{\partial \tau^{(y)}}{\partial x} - \frac{\partial \tau^{(x)}}{\partial y}\normalsize \Big) - v \beta = \Large\frac{1}{\rho}\frac{\partial}{\partial z} \Big( \frac{\partial \tau^{(y)}}{\partial x} - \frac{\partial \tau^{(x)}}{\partial y} \normalsize \Big) + \Large\frac{\beta}{\rho f} \frac{\partial \tau^{(x)}}{\partial z} \normalsize= f \Big( \Large\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} \normalsize \Big) = - f \Large\frac{\partial w}{\partial z}\normalsize . \qquad (12)[/math]
This equation can be integrated from the Ekman depth [math]-D_E[/math] to the surface. Neglecting shear stresses at the Ekman depth with respect to the surface shear stresses, the following estimate for the vertical velocity [math]w_E[/math] at the Ekman depth is obtained:
[math]w_E = \Large \frac{1}{\rho f} \Big( \frac{\partial}{\partial x}\normalsize \tau_w^{(y)} - \Large\frac{\partial}{\partial y}\normalsize \tau_w^{(x)} \Big) + \Large\frac{\beta}{\rho f^2}\normalsize \tau_w^{(x)} . \qquad (13)[/math]
This expression has a singularity at the equator where [math]f=0[/math], which is due to the model simplifications. The formula (13) shows that the Ekman transport mechanism can generate substantial vertical water motions near the equator. The subtropical trade winds which are oriented E-W ([math]\tau_w^{(x)} \lt 0[/math]) increase towards the equator ([math]f^{-1} \, \partial \tau_w^{(x)} / \partial y [/math] > 0). This produces downwelling currents ([math]w_E \lt 0[/math]) in the surface Ekman layer of the subtropical ocean. The transition zones from the low-latitude trade winds to the westerlies at higher latitudes can be considered large-scale anticyclonic gyres with corresponding downwelling currents[2], see Ocean circulation.
Related articles
References
- ↑ Ekman, V.W. 1905. On the influence of the Earth’s rotation on ocean-currents. Arch. Math. Astron. Phys. 2: 1-52
- ↑ 2.0 2.1 2.2 Chereskin, T.K. and Price, J.F. 2001. Ekman transport and pumping. Encyclopedia of Ocean Science, vol. 2, p. 809-815. Elsevier
- ↑ Pinet P.R. 1998.Invitation to Oceanography. Jones and Barlett Publishers. p. 508
- ↑ Price, J.F. and Sundermeyer, M.A. 1999. Stratified Ekman layers. J. Geophys. Res. 104: 20.467-20.494
- ↑ Liao, E., Resplandy, L., Liu, J. and Bowman, K. W. 2020. Amplification of the ocean carbon sink during El Niños: Role of poleward Ekman transport and influence on atmospheric CO2. Global Biogeochemical Cycles 34, e2020GB006574
Please note that others may also have edited the contents of this article.
|