Difference between revisions of "Measurements of biodiversity"
Dronkers J (talk | contribs) |
Dronkers J (talk | contribs) |
||
| Line 38: | Line 38: | ||
===Species richness indices=== | ===Species richness indices=== | ||
| − | Species richness <math> | + | Species richness <math>S</math> is the simplest measure of biodiversity and is simply a count of the number of different species in a given area. This measure is strongly dependent on sampling size and effort. Two species richness indices try to account for this problem: |
====Margalef’s diversity index<ref> Clifford H.T. and Stephenson W. 1975. An introduction to numerical classification. London: Academic Express.</ref>==== | ====Margalef’s diversity index<ref> Clifford H.T. and Stephenson W. 1975. An introduction to numerical classification. London: Academic Express.</ref>==== | ||
| − | <math>D_{Mg} = \Large\frac{ | + | <math>D_{Mg} = \Large\frac{S-1}{\ln N}</math>, |
| − | where <math> | + | where <math>N</math> = the total number of individuals in the sample and <math>S</math> = the number of species recorded. |
====Menhinick’s diversity index<ref>Whittaker R.H. 1977. Evolution of species diversity in land communities. Evolutionary Biol. 10: 1-67 </ref>==== | ====Menhinick’s diversity index<ref>Whittaker R.H. 1977. Evolution of species diversity in land communities. Evolutionary Biol. 10: 1-67 </ref>==== | ||
| − | <math>D_{Mn} = \Large\frac{ | + | <math>D_{Mn} = \Large\frac{S}{\sqrt{N}}</math>. |
| Line 58: | Line 58: | ||
===Parametric indices=== | ===Parametric indices=== | ||
====The log series index==== | ====The log series index==== | ||
| − | The log series index <math>\alpha\,</math> is a parameter of the log series model that was derived by Fisher et al (1943<ref name="Fisher">Fisher, R. A., Corbet, A. S. and Williams, C. B. 1943. The relation between the number of species and the number of individuals in a random sample of an animal population. Journal of Animal Ecology 12: 42-58</ref>) from statistical arguments for very heterogeneous | + | The log series index <math>\alpha\,</math> is a parameter of the log series model that was derived by Fisher et al (1943<ref name="Fisher">Fisher, R. A., Corbet, A. S. and Williams, C. B. 1943. The relation between the number of species and the number of individuals in a random sample of an animal population. Journal of Animal Ecology 12: 42-58</ref>) from statistical arguments for very heterogeneous communities (see also [[#The log-series distribution|log-series distribution]]). The parameter <math>\alpha\,</math> is a characteristic of the community and independent of sample size. It describes the way in which the individuals are divided among the species, which is a measure of diversity. The attractive properties of this diversity index are: it provides a good discrimination between sites, it is not very sensitive to density fluctuations and it is normally distributed such that confidence limits can be attached to <math>\alpha\,</math>. |
The log series takes the form: | The log series takes the form: | ||
| − | <math>\alpha\,x \, , \quad \Large\frac{\alpha\, x^2}{2} \, , \frac{\alpha\, x^3}{3} , \, ...\, , \frac{\alpha\, x^ | + | <math>\alpha\,x \, , \quad \Large\frac{\alpha\, x^2}{2} \, , \frac{\alpha\, x^3}{3} , \, ...\, , \frac{\alpha\, x^n}{n} , …. \qquad</math> or <math>s(n)= \frac{\alpha\, x^n}{n}</math>, |
| − | where <math> | + | where <math>s(n)</math> is the number of species to have <math>n</math> individuals. Since <math>0 < \,x < 1</math> and <math>\alpha\,</math> and <math>\,x</math> are presumed to be constant, the expected number of species will be the highest for the first abundance class comprising a single individual. The total number of species <math>S</math> for a large sample with many species can be approximated by |
| − | <math> | + | <math>S \approx \sum_{n=1}^{\infty} s(n) = \alpha \sum_{n=1}^{\infty} x^n / n = - \alpha \, \ln(1-x)</math>. |
The total number of individual can be approximated by | The total number of individual can be approximated by | ||
| − | <math>n \ | + | <math> N \approx \sum_{n=1}^{\infty} n s(n) = \alpha \sum_{n=1}^{\infty} x^n = \alpha \, x / (1-x)</math>. |
| + | |||
| + | The values of <math>\,x</math> and <math>\alpha</math> can be estimated from these two equations by counting the total numbers <math>N</math> and <math>S</math> of the sample. It should be noted that, unless the number of species increases linearly with the sample size, the parameter <math>x</math> depends on the sample size. The distribution over species thus changes with sample size. | ||
| + | |||
| + | ====The log-normal distribution==== | ||
| + | Preston <ref> Preston, F.W. 1948. The commonness and rarity of species. Ecology 29: 254–283</ref> first suggested to use a log-normal distribution for the description of species-abundances distributions. This is a normal (Gaussian) distribution for the parameter <math>y=\ln(n)</math>, the logarithm of the species abundance <math>n</math> (= the number of individuals belonging to the same species). Samples are considered with a large number of species and a large number of individuals. The log-normal distribution allows variation of <math>n</math> from 1 to infinity; then the corresponding values of <math>y</math> are in the range <math>[-\infty, +\infty]</math>. The distribution specifies the relative number of species <math>s(y)dy</math> that may be expected with abundances <math>n</math> in the interval <math>[y,y+dy]</math>; it is given by | ||
| + | |||
| + | <math>s(y)dy = \Large\frac{S}{\sigma \sqrt{2 \pi}}\normalsize \, \exp(-\Large\frac{y-\mu)^2}{2 \sigma^2}\normalsize) \, dy</math>, | ||
| + | |||
| + | where <math>S</math> is the total number of species and where <math>\mu</math> and <math>\sigma</math> are related to the average number of individuals per species and to the variance, | ||
| + | |||
| + | <math>\overline{n} = \Large\frac{N}{S}\normalsize = \exp(\mu + ½ \sigma^2) , \qquad \overline{(n-\overline{n})^2} = (\exp(\sigma^2) – 1)\, \exp(2 \mu +\sigma^2)</math>. | ||
| + | |||
| + | Contrary to the log series, this distribution does not assume that species with the lowest abundance are most numerous. | ||
| + | |||
| + | Magurran and Henderson (2003<ref name=MH>Magurran, A.E. and Henderson, P.A. 2003. Explaining the excess of rare species in natural species abundance distributions. Nature 422: 714–716</ref>) explain the difference between the log-series distribution and the log-normal distribution as follows, based on a long-term (21-year) data set, from an estuarine fish community: | ||
| + | "The ecological community can be separated into two components. Core species, which are persistent, abundant and biologically associated with estuarine habitats, are log normally distributed. Occasional species occur infrequently in the record, are typically low in abundance and have different habitat requirements; they follow a log series distribution. These distributions are overlaid, producing the negative skew that characterizes real data sets." | ||
| + | |||
| + | |||
| + | [[Image:SpeciesAbundance.jpg|thumb|700px|center|Fig. 2. The abundance distribution of species of the fish community of Hinkley Point, Bristol Channel. Occasional species (left) have a distribution of the log-series type, persistent species (middle) have a distribution of the log-normal type. The overall distribution (right) more similar to the log-series type. Adapted after Magurran and Henderson (2003<ref name=MH/>.)]] | ||
| − | |||
| Line 83: | Line 101: | ||
It assumed that individuals are randomly sampled from a very large community, and that all species are represented in the sample. The Shannon index is calculated from the equation | It assumed that individuals are randomly sampled from a very large community, and that all species are represented in the sample. The Shannon index is calculated from the equation | ||
| − | <math>H' = -\sum_{i=1}^ | + | <math>H' = -\sum_{i=1}^S p_i \, \ln p_i</math> , |
| − | where <math>p_i</math> is the probability to find <math>n_i= n p_i</math> individuals in the <math>i</math>-th species (<math>\sum_{i=1}^ | + | where <math>p_i</math> is the probability to find <math>n_i= n p_i</math> individuals in the <math>i</math>-th species (<math>\sum_{i=1}^S p_i = 1</math>). The number of individuals <math>n_i</math> of species <math>i</math> is generally called the '''abundance''' of this species. |
====Brillouin index==== | ====Brillouin index==== | ||
Where the randomness cannot be guaranteed, for example when certain species are preferentially sampled, the Brillouin index<ref> Pielou E.C. 1969. An introduction to mathematical ecology. New York: Wiley.</ref><ref name="Pielou"/> is a more appropriate form of the information index. It is calculated as follows: | Where the randomness cannot be guaranteed, for example when certain species are preferentially sampled, the Brillouin index<ref> Pielou E.C. 1969. An introduction to mathematical ecology. New York: Wiley.</ref><ref name="Pielou"/> is a more appropriate form of the information index. It is calculated as follows: | ||
| − | <math>H = \Large\frac{1}{ | + | <math>H = \Large\frac{1}{N}\normalsize [ \ln(N!) - \sum_{i=1}^S \ln(n_i !)] , </math> |
| − | in which <math> n_i != 1 \times 2 \times 3 \times ... \times n_i</math> and <math>n_i </math> = the number of individuals in species <math>i</math> and <math> | + | in which <math> n_i != 1 \times 2 \times 3 \times ... \times n_i</math> and <math>n_i </math> = the number of individuals in species <math>i</math> and <math>N</math> is the total number of individuals in the community. |
====Simpson ’s index==== | ====Simpson ’s index==== | ||
One of the best known and earliest evenness measures is the Simpson ’s index<ref>Simpson E.H. 1949. Measurement of diversity. Nature 163: 688.</ref> which is given by: | One of the best known and earliest evenness measures is the Simpson ’s index<ref>Simpson E.H. 1949. Measurement of diversity. Nature 163: 688.</ref> which is given by: | ||
| − | <math>\gamma\, = \sum_{i=1}^ | + | <math>\gamma\, = \sum_{i=1}^S p_i^2</math>. |
| − | This index is used for large, sampled communities. Simpson’s index expresses the probability that any two individuals drawn at random from an infinitely large community belong to the same species. If all species are equally represented in the sample, then <math>p_i=1/ | + | This index is used for large, sampled communities. Simpson’s index expresses the probability that any two individuals drawn at random from an infinitely large community belong to the same species. If all species are equally represented in the sample, then <math>p_i=1/S</math> or <math>\gamma=1/S</math>. |
====Pielou index==== | ====Pielou index==== | ||
Another evenness index was proposed by Pielou (1966<ref>Pielou, E.C. 1966. The measurement of diversity in different types of biological collection. Journal of Theoretical Biology 13: 131–144</ref>). The '''Pielou index''' <math>J'</math> is defined as | Another evenness index was proposed by Pielou (1966<ref>Pielou, E.C. 1966. The measurement of diversity in different types of biological collection. Journal of Theoretical Biology 13: 131–144</ref>). The '''Pielou index''' <math>J'</math> is defined as | ||
| − | <math>J' \, = \, H' / \ln( | + | <math>J' \, = \, H' / \ln(S) </math>. |
If all species are represented in equal numbers in the sample, then <math>J'=1</math>. If one species strongly dominates <math>J'</math> is close to zero. | If all species are represented in equal numbers in the sample, then <math>J'=1</math>. If one species strongly dominates <math>J'</math> is close to zero. | ||
| − | ====Hill numbers==== | + | ====Hill numbers====large |
The Hill numbers<ref> Hill, M.O. 1973. Diversity and evenness: a unifying notation and its consequences. Ecology 54: 427–473</ref> show the relation between the species-richness indices and the evenness-indices. Hill defined a set of diversity number of different order. The diversity number of order <math>a</math> is defined as: | The Hill numbers<ref> Hill, M.O. 1973. Diversity and evenness: a unifying notation and its consequences. Ecology 54: 427–473</ref> show the relation between the species-richness indices and the evenness-indices. Hill defined a set of diversity number of different order. The diversity number of order <math>a</math> is defined as: | ||
| − | <math>H_a = (\sum_{i=1}^ | + | <math>H_a = (\sum_{i=1}^S p_i^a)^{\large\frac{1}{1-a}}</math> , |
| − | where <math>p_i</math> = the proportional abundance of species <math>i</math> in the sample and <math>a</math> = the order in which the index is dependent of rare species. | + | where <math>p_i</math> = the proportional abundance of species <math>i</math> in the sample and <math>a</math> = the order in which the index is dependent of rare species. For very large positive values of <math>a<math> the Hill number takes into account only the most abundant species, whereas for very large negative values the Hill number takes in account only the rarest species. |
The most common Hill numbers are | The most common Hill numbers are | ||
| − | <math>H_0 = \, | + | <math>H_0 = \, S </math>, |
<math>H_1 = \exp{H'} </math> (the limit of <math>H_a</math> for <math>a \to 1</math> corresponds to the exponential of the Shannon-Wiener diversity index, see appendix A2), | <math>H_1 = \exp{H'} </math> (the limit of <math>H_a</math> for <math>a \to 1</math> corresponds to the exponential of the Shannon-Wiener diversity index, see appendix A2), | ||
| Line 123: | Line 141: | ||
<math>H_2 =\Large\frac{1}{\gamma}</math> (the reciprocal of Simpson’s <math>\gamma\, </math>) . | <math>H_2 =\Large\frac{1}{\gamma}</math> (the reciprocal of Simpson’s <math>\gamma\, </math>) . | ||
| − | If all species are represented in equal numbers in the sample <math>H_0=H_1=H_2= | + | If all species are represented in equal numbers in the sample <math>H_0=H_1=H_2=S</math>. |
| Line 134: | Line 152: | ||
• Taxonomic diversity (<math>\Delta</math>) reflects the average taxonomic distance between any two organisms, chosen at random from a sample. The distance can be seen as the length of the path connecting these two organisms through a phylogenetic tree or a Linnean classification<ref name=WC/>. This index includes aspects of taxonomic relatedness and evenness, | • Taxonomic diversity (<math>\Delta</math>) reflects the average taxonomic distance between any two organisms, chosen at random from a sample. The distance can be seen as the length of the path connecting these two organisms through a phylogenetic tree or a Linnean classification<ref name=WC/>. This index includes aspects of taxonomic relatedness and evenness, | ||
| − | <math>\Delta = \Large\frac{ \sum\sum_{i<j} \, \omega_{ij} \, n_i n_j}{ | + | <math>\Delta = \Large\frac{ \sum\sum_{i<j} \, \omega_{ij} \, n_i n_j}{N(N-1)/2} </math>, |
| − | where <math>n_i=n p_i</math> denotes the abundance of the <math>i</math>-th species in the sample (<math>\sum_{i=1}^ | + | where <math>n_i=n p_i</math> denotes the abundance of the <math>i</math>-th species in the sample (<math>\sum_{i=1}^S n_i =N</math> = the number of individuals in the sample) and <math>\omega_{ij}</math> is the 'distinctness weight' given to the path length (number of steps) linking species <math>i</math> and <math>j</math> in the hierarchical classification. (The path length for two individuals of the same species is zero). |
• Taxonomic distinctness (<math>\Delta^*</math>) is the average path length between two randomly chosen but taxonomically different organisms. This measure is measure of pure taxonomic relatedness, | • Taxonomic distinctness (<math>\Delta^*</math>) is the average path length between two randomly chosen but taxonomically different organisms. This measure is measure of pure taxonomic relatedness, | ||
| Line 146: | Line 164: | ||
Journal of Applied Ecology 35 (4): 523-531</ref>, | Journal of Applied Ecology 35 (4): 523-531</ref>, | ||
| − | <math>\Delta^+= \Large\frac{\sum\sum_{i<j} \, \omega_{ij}}{ | + | <math>\Delta^+= \Large\frac{\sum\sum_{i<j} \, \omega_{ij}}{S(S-1)/2}</math>. |
===Functional diversity=== | ===Functional diversity=== | ||
| Line 153: | Line 171: | ||
| − | ==Species-Abundance distributions<ref>Heip, C.H.R., Herman, P.M.J. and Soetaert, K. 1998. Indices de diversité et régularité. [Indices of diversity and evenness]. Océanis (Doc. Océanogr.) 24(4): 67-87</ref>== | + | ==Species-Abundance distributions<ref name=H>Heip, C.H.R., Herman, P.M.J. and Soetaert, K. 1998. Indices de diversité et régularité. [Indices of diversity and evenness]. Océanis (Doc. Océanogr.) 24(4): 67-87</ref>== |
| − | Nearly all diversity and evenness indices are based on the relative abundance of species, thus on estimates of <math>p_i</math> in which <math>p_i = n_i / | + | Nearly all diversity and evenness indices are based on the relative abundance of species, thus on estimates of <math>p_i</math> in which <math>p_i = n_i / N </math>, with <math>n_i</math> the abundance of the <math>i</math>-th species in the sample and <math>N = \sum _{i = 1}^S \, n_i</math> with <math>S</math> the total number of species in the sample. |
When recording the abundance of different species in a sample, it is invariably found that some species are rare, whereas others are more abundant. This feature of ecological communities is found independently of the taxonomic group or the area investigated. An important goal of ecology is to describe these consistent patterns in different communities, and explain them in terms of interactions with the biotic and abiotic environment. | When recording the abundance of different species in a sample, it is invariably found that some species are rare, whereas others are more abundant. This feature of ecological communities is found independently of the taxonomic group or the area investigated. An important goal of ecology is to describe these consistent patterns in different communities, and explain them in terms of interactions with the biotic and abiotic environment. | ||
| Line 165: | Line 183: | ||
2. '''The <math>k</math>-dominance plot''' shows the cumulative percentage (the percentage of the <math>k</math>-th most dominant plus all more dominant species) in relation to species (<math>k</math>) rank or log species (<math>k</math>) rank. | 2. '''The <math>k</math>-dominance plot''' shows the cumulative percentage (the percentage of the <math>k</math>-th most dominant plus all more dominant species) in relation to species (<math>k</math>) rank or log species (<math>k</math>) rank. | ||
| − | 3. '''The Lorenzen curve''' is based on the <math>k</math>-dominance plot but the species rank <math>k</math> is transformed to <math> (k/ | + | 3. '''The Lorenzen curve''' is based on the <math>k</math>-dominance plot but the species rank <math>k</math> is transformed to <math> (k/S) \times 100</math> to facilitate comparison between communities with different numbers of species. |
| − | 4. '''The collector’s curve''' addresses a different problem. When the sampling effort is increased, and thus the number of | + | 4. '''The collector’s curve''' addresses a different problem. When the sampling effort is increased, and thus the number of individuals <math>N</math> caught, new species will appear in the collection. A collector’s curve expresses the number of species as a function of the number of specimens caught. As more specimens are caught, a collector’s curve can reach an asymptotic value. However, this hardly does occur in practice due to the vague boundaries of ecological communities: as the sampling effort increases, the number of different patches increases as well. |
5. '''The species-abundance distribution''' plots the number of species that are represented by <math>1,2, … , n </math> individuals against the corresponding abundance. This plot can only be drawn if the collection is large and contains many species. The species are generally grouped in logarithmic density classes. | 5. '''The species-abundance distribution''' plots the number of species that are represented by <math>1,2, … , n </math> individuals against the corresponding abundance. This plot can only be drawn if the collection is large and contains many species. The species are generally grouped in logarithmic density classes. | ||
| Line 182: | Line 200: | ||
==Species-Abundance models<ref name="Magurran"/> == | ==Species-Abundance models<ref name="Magurran"/> == | ||
| − | + | Besides the log-series and log-normal models, also other models have been developed to describe species abundance data (Fig. 4). These models are based on species abundance observed in diverse ecosystems. | |
| − | + | ||
| + | [[Image:Abundance.jpg|thumb|right|300px|Fig. 4. The four main species- abundance models]] | ||
| + | |||
====The niche preemption model or the geometric model==== | ====The niche preemption model or the geometric model==== | ||
It assumes that a species preempts a fraction <math>k</math> of a limiting resource, a second species the same fraction <math>k</math> of the remainder and so on. If the abundances are proportional to their share of the resource, the ranked abundances list is given by geometric series (see appendix A3): | It assumes that a species preempts a fraction <math>k</math> of a limiting resource, a second species the same fraction <math>k</math> of the remainder and so on. If the abundances are proportional to their share of the resource, the ranked abundances list is given by geometric series (see appendix A3): | ||
| − | <math>\Large\frac{n_i}{ | + | <math>\Large\frac{n_i}{N}\normalsize=\Large\frac{k(1-k)^{(i-1)}}{1-(1-k)^S}</math>, |
| − | where <math> | + | where <math>S</math> is the number of the species in the community. For large values of <math>S</math> this distribution depends only on the parameter <math>k</math>. In this case the Shannon-Wiener index is given by <math>H' \approx ((k-1)/k) \ln(1-k) - \ln(k)</math>. For small values of <math>k</math> the index is large (high biodiversity) and for values of <math>k</math> close to 1 the index is close to zero (low biodiversity). |
| − | The geometric model gives a straight line on a plot of log abundance against rank (species sequence). It is not very often found in nature, only in early successional stages or in species poor environments | + | The geometric model gives a straight line on a plot of log abundance against rank (species sequence). It is not very often found in nature, only in early successional stages or in species poor environments<ref name=H/>. |
| − | |||
| − | |||
| − | |||
====The broken stick model or the negative exponential distribution==== | ====The broken stick model or the negative exponential distribution==== | ||
| − | In this model a limiting resource is compared with a stick, broken in <math> | + | In this model a limiting resource is compared with a stick, broken in <math>S</math> parts at <math>S-1</math> randomly located points. The length of the parts is taken as representative for the density of the <math>S</math> species subdividing the limiting resource. If the species are ranked according to abundance, the expected abundance <math>n_i</math> of species <math>i</math> is given by<ref>McArthur, R.H. 1957. On the relative abundance of bird species. Proc. Natl. Acad. Sci. USA 43: 293-295</ref>: |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <math> | + | <math>\Large\frac{n_i}{N}\normalsize= \Large\frac{1}{S}\normalsize \sum_{k = i}^S \frac{1}{k} </math>. |
| − | + | This distribution satisfies the condition <math>N = \sum_{i=1}^S n_i </math>. The dependence on the single parameter <math>S</math> is weak for large values of <math>S</math>. For large values of <math>S</math> the Shannon-Wiener index is close to <math>H' \approx ln(S)</math>. | |
| − | < | + | The negative exponential distribution is not often found in nature; it describes a too even distribution of individuals over species to be a good representation of natural communities<ref name=H/>. |
==Appendix A1== | ==Appendix A1== | ||
| − | The Shannon-Wiener diversity index is a measure of the information (in fact, the 'lack of information', or 'uncertainty' or 'information entropy') represented by a sample, where information is defined as the minimum length of a string of digits necessary to describe the sample. The minimum length of a string of digits to describe a number is proportional to the logarithm of this number. All the ways in which <math> | + | The Shannon-Wiener diversity index is a measure of the information (in fact, the 'lack of information', or 'uncertainty' or 'information entropy') represented by a sample, where information is defined as the minimum length of a string of digits necessary to describe the sample. The minimum length of a string of digits to describe a number is proportional to the logarithm of this number. All the ways in which <math>N</math> individuals can be distributed in numbers <math>n_1, n_2, …, n_S</math> for the species <math>1, 2, …., S</math> are equivalent and thus provide no information. With this definition, a measure of the information uncertainty in a large sample is given by the logarithm of the number <math>P</math> of all different permutations of individuals that give the same distribution of individuals over species. If <math>P</math> is large, the sample can be ordered in many distinct equivalent ways and thus conveys few information (= high information entropy = high diversity). This is the case, for example, if all <math>N</math> individuals in a sample belong to different species. The number of distinct permutations is then equal to <math>P=N!</math> (the first individual in an ordered sample can be chosen in <math>N</math> ways, the second in <math>N-1</math> ways and so on). If there are <math>n_1</math> individuals of species 1, <math>n_2</math> individuals of species 2, and so on, then the number of equivalent distinct permutations is <math>P = N!/(n_1! \times n_2! \times . . . . \times n_S!)</math>. Taking the logarithm gives <math>N \times</math> the Brillouin index <math>H</math>. Assuming that the numbers <math>N, n_1, n_2, ….</math> are very large, one can approximate <math>\ln(n_i!) \approx n_i\, \ln(n_i) </math>. This gives <math>\ln(P) \approx N \, \ln(N) – n_1 \, \ln(n_1) – n_2\, \ln(n_2) - ….. n_S \, \ln(n_S) </math>. For large representative samples the probability of occurrence of species <math>i</math> is given by <math>p_i=n_i/N</math>. We further have <math>\sum_{i=1}^{S} p_i=1</math>. Substitution gives <math>\ln(P) \approx -N \sum_{i=1}^{S} p_i \, \ln(p_i)</math>, which is <math>N \times</math> the Shannon-Wiener index <math>H'</math>. Division by <math>N</math> makes the index independent of the sample size. |
| − | Another interpretation of the Shannon-Wiener index is: the mean number of digits required for describing the probability <math>p_i</math> to find <math>n_i</math> individuals of species <math>i</math> in the sample of <math> | + | Another interpretation of the Shannon-Wiener index is: the mean number of digits required for describing the probability <math>p_i</math> to find <math>n_i</math> individuals of species <math>i</math> in the sample of <math>N</math> individuals. The number of digits for describing the probability <math>p_i</math> is proportional to <math>-\ln(p_i)</math> (the rarer the species, the smaller <math>p_i</math> and the more digits are needed). The mean is obtained by taking the weighted sum of the number of digits: <math>H'= - \sum_{i=1}^S p_i \ln(p_i)</math>. |
==Appendix A2== | ==Appendix A2== | ||
Take <math>a=1+\epsilon</math> and <math>\epsilon \to 0</math>, then <math>p_i^a \to p_i+\epsilon \large\frac{d}{d \epsilon} p_i^{1+\epsilon}\normalsize \approx p_i + \epsilon p_i \ln p_i</math>. | Take <math>a=1+\epsilon</math> and <math>\epsilon \to 0</math>, then <math>p_i^a \to p_i+\epsilon \large\frac{d}{d \epsilon} p_i^{1+\epsilon}\normalsize \approx p_i + \epsilon p_i \ln p_i</math>. | ||
| − | Because <math>\sum_{i=1}^ | + | Because <math>\sum_{i=1}^S p_i = 1</math>, we have |
| − | <math>H_1 = \lim_{\epsilon \to 0} (1 + \epsilon \sum_{i=1}^ | + | <math>H_1 = \lim_{\epsilon \to 0} (1 + \epsilon \sum_{i=1}^S p_i \ln p_i)^{-1/\epsilon} = \exp(-\sum_{i=1}^S p_i \ln p_i)</math>. |
==Appendix A3== | ==Appendix A3== | ||
| − | According to the assumptions underlying the model, the numbers <math>\, n_1, n_2, …., | + | According to the assumptions underlying the model, the numbers <math>\, n_1, n_2, …., n_S \, </math> of species <math>\, 1, 2, …., S \,</math> are |
| − | <math>n_1=Ck, \; n_2= Ck(1-k), \; n_3=Ck(1-k-k(1-k))=Ck(1-k)^2, …., \; | + | <math>n_1=Ck, \; n_2= Ck(1-k), \; n_3=Ck(1-k-k(1-k))=Ck(1-k)^2, …., \; n_S=Ck(1-k)^{(S-1)} </math>. |
| − | We have <math> | + | We have <math>N = \sum_{i=1}^S n_i = Ck\sum_{i=1}^S (1-k)^{(i-1)} = C(1-(1-k)^S) </math>, hence <math>C=\Large\frac{N}{1-(1-k)^S}</math>. |
Revision as of 22:23, 5 October 2020
A variety of objective measures have been created in order to empirically measure biodiversity. The basic idea of a diversity index is to obtain a quantitative estimate of biological variability that can be used to compare biological entities, composed of diverse components, in space or in time. It is important to distinguish ‘richness’ from ‘diversity’. Diversity usually implies a measure of both species number and ‘equitability’ (or ‘evenness’). Three types of indices can be distinguished:
1. Species richness indices: Species richness is a measure for the total number of the species in a community (examples Fig. 1). However, complete inventories of all species present at a certain location, is an almost unattainable goal in practical applications.
2. Evenness indices: Evenness expresses how evenly the individuals in a community are distributed among the different species (examples Fig.2).
3. Taxonomic indices: These indices take into account the taxonomic relation between different organisms in a community. Taxonomic diversity, for example, reflects the average taxonomic distance between any two organisms, chosen at random from a sample. The distance can be seen as the length of the path connecting these two organisms along the branches of a phylogenetic tree.
These three types of indices can be used on different spatial scales [1]:
- Alpha diversity refers to diversity within a particular area, community or ecosystem, and is usually measured by counting the number of taxa within the ecosystem (usually species level);
- Beta diversity is species diversity between ecosystems; this involves comparing the number of taxa that are unique to each of the ecosystems. For example, the diversity of mangroves versus the diversity of seagrass beds;
- Gamma diversity is a measure of the overall diversity for different ecosystems within a region. For example, the diversity within the coastal region of Gazi Bay in Kenia.
Contents
- 1 Diversity measurement is based on three assumptions[2]
- 2 Diversity measures
- 3 Species-Abundance distributions[17]
- 4 Species-Abundance models[2]
- 5 Appendix A1
- 6 Appendix A2
- 7 Appendix A3
- 8 See also
- 9 Further reading
- 10 References
Diversity measurement is based on three assumptions[2]
1. All species are equal: this means that richness measurement makes no distinctions amongst species and threat the species that are exceptionally abundant in the same way as those that are extremely rare species. The relative abundance of species in an assemblage is the only factor that determines its importance in a diversity measure.
2. All individuals are equal: this means that there is no distinction between the largest and the smallest individual, in practice however the smallest animals can often escape for example by sampling with nets.
Taxonomic and functional diversity measures, however, do not necessarily treat all species and individuals as equal.
3. Species abundance has been recorded in using appropriate and comparable units. It is clearly unwise to use different types of abundance measure, such as the number of individuals and the biomass, in the same investigation. Diversity estimates based on different units are not directly comparable.
Diversity measures
Species richness indices
Species richness [math]S[/math] is the simplest measure of biodiversity and is simply a count of the number of different species in a given area. This measure is strongly dependent on sampling size and effort. Two species richness indices try to account for this problem:
Margalef’s diversity index[3]
[math]D_{Mg} = \Large\frac{S-1}{\ln N}[/math],
where [math]N[/math] = the total number of individuals in the sample and [math]S[/math] = the number of species recorded.
Menhinick’s diversity index[4]
[math]D_{Mn} = \Large\frac{S}{\sqrt{N}}[/math].
Despite the attempt to correct for sample size, both measures remain strongly influenced by sampling effort. Nonetheless they are intuitively meaningful indices and can play a useful role in investigations of biological diversity.
Heterogeneity measures
Heterogeneity measures are those that combine the richness and the evenness component of diversity. Heterogeneity measures fall into two categories: parametric indices, which are based on a parameter of a species abundance model, and nonparametric indices, that make no assumptions about the underlying distributions of species abundances.
Parametric indices
The log series index
The log series index [math]\alpha\,[/math] is a parameter of the log series model that was derived by Fisher et al (1943[5]) from statistical arguments for very heterogeneous communities (see also log-series distribution). The parameter [math]\alpha\,[/math] is a characteristic of the community and independent of sample size. It describes the way in which the individuals are divided among the species, which is a measure of diversity. The attractive properties of this diversity index are: it provides a good discrimination between sites, it is not very sensitive to density fluctuations and it is normally distributed such that confidence limits can be attached to [math]\alpha\,[/math].
The log series takes the form:
[math]\alpha\,x \, , \quad \Large\frac{\alpha\, x^2}{2} \, , \frac{\alpha\, x^3}{3} , \, ...\, , \frac{\alpha\, x^n}{n} , …. \qquad[/math] or [math]s(n)= \frac{\alpha\, x^n}{n}[/math],
where [math]s(n)[/math] is the number of species to have [math]n[/math] individuals. Since [math]0 \lt \,x \lt 1[/math] and [math]\alpha\,[/math] and [math]\,x[/math] are presumed to be constant, the expected number of species will be the highest for the first abundance class comprising a single individual. The total number of species [math]S[/math] for a large sample with many species can be approximated by
[math]S \approx \sum_{n=1}^{\infty} s(n) = \alpha \sum_{n=1}^{\infty} x^n / n = - \alpha \, \ln(1-x)[/math].
The total number of individual can be approximated by
[math] N \approx \sum_{n=1}^{\infty} n s(n) = \alpha \sum_{n=1}^{\infty} x^n = \alpha \, x / (1-x)[/math].
The values of [math]\,x[/math] and [math]\alpha[/math] can be estimated from these two equations by counting the total numbers [math]N[/math] and [math]S[/math] of the sample. It should be noted that, unless the number of species increases linearly with the sample size, the parameter [math]x[/math] depends on the sample size. The distribution over species thus changes with sample size.
The log-normal distribution
Preston [6] first suggested to use a log-normal distribution for the description of species-abundances distributions. This is a normal (Gaussian) distribution for the parameter [math]y=\ln(n)[/math], the logarithm of the species abundance [math]n[/math] (= the number of individuals belonging to the same species). Samples are considered with a large number of species and a large number of individuals. The log-normal distribution allows variation of [math]n[/math] from 1 to infinity; then the corresponding values of [math]y[/math] are in the range [math][-\infty, +\infty][/math]. The distribution specifies the relative number of species [math]s(y)dy[/math] that may be expected with abundances [math]n[/math] in the interval [math][y,y+dy][/math]; it is given by
[math]s(y)dy = \Large\frac{S}{\sigma \sqrt{2 \pi}}\normalsize \, \exp(-\Large\frac{y-\mu)^2}{2 \sigma^2}\normalsize) \, dy[/math],
where [math]S[/math] is the total number of species and where [math]\mu[/math] and [math]\sigma[/math] are related to the average number of individuals per species and to the variance,
[math]\overline{n} = \Large\frac{N}{S}\normalsize = \exp(\mu + ½ \sigma^2) , \qquad \overline{(n-\overline{n})^2} = (\exp(\sigma^2) – 1)\, \exp(2 \mu +\sigma^2)[/math].
Contrary to the log series, this distribution does not assume that species with the lowest abundance are most numerous.
Magurran and Henderson (2003[7]) explain the difference between the log-series distribution and the log-normal distribution as follows, based on a long-term (21-year) data set, from an estuarine fish community: "The ecological community can be separated into two components. Core species, which are persistent, abundant and biologically associated with estuarine habitats, are log normally distributed. Occasional species occur infrequently in the record, are typically low in abundance and have different habitat requirements; they follow a log series distribution. These distributions are overlaid, producing the negative skew that characterizes real data sets."
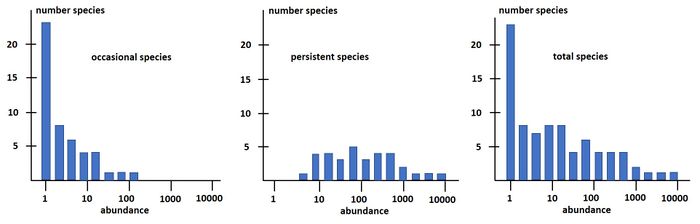
Non-parametric indices
The first two indices are based on information theory. These indices are based on the rationale that the diversity in a natural system can be measured in a similar way to the information contained in a code or message (see Appendix A1).
Shannon-Wiener diversity index
The most widely used diversity index in the ecological literature is the Shannon-Wiener diversity index[8][9].
It assumed that individuals are randomly sampled from a very large community, and that all species are represented in the sample. The Shannon index is calculated from the equation
[math]H' = -\sum_{i=1}^S p_i \, \ln p_i[/math] ,
where [math]p_i[/math] is the probability to find [math]n_i= n p_i[/math] individuals in the [math]i[/math]-th species ([math]\sum_{i=1}^S p_i = 1[/math]). The number of individuals [math]n_i[/math] of species [math]i[/math] is generally called the abundance of this species.
Brillouin index
Where the randomness cannot be guaranteed, for example when certain species are preferentially sampled, the Brillouin index[10][9] is a more appropriate form of the information index. It is calculated as follows:
[math]H = \Large\frac{1}{N}\normalsize [ \ln(N!) - \sum_{i=1}^S \ln(n_i !)] , [/math]
in which [math] n_i != 1 \times 2 \times 3 \times ... \times n_i[/math] and [math]n_i [/math] = the number of individuals in species [math]i[/math] and [math]N[/math] is the total number of individuals in the community.
Simpson ’s index
One of the best known and earliest evenness measures is the Simpson ’s index[11] which is given by:
[math]\gamma\, = \sum_{i=1}^S p_i^2[/math].
This index is used for large, sampled communities. Simpson’s index expresses the probability that any two individuals drawn at random from an infinitely large community belong to the same species. If all species are equally represented in the sample, then [math]p_i=1/S[/math] or [math]\gamma=1/S[/math].
Pielou index
Another evenness index was proposed by Pielou (1966[12]). The Pielou index [math]J'[/math] is defined as
[math]J' \, = \, H' / \ln(S) [/math].
If all species are represented in equal numbers in the sample, then [math]J'=1[/math]. If one species strongly dominates [math]J'[/math] is close to zero.
====Hill numbers====large The Hill numbers[13] show the relation between the species-richness indices and the evenness-indices. Hill defined a set of diversity number of different order. The diversity number of order [math]a[/math] is defined as:
[math]H_a = (\sum_{i=1}^S p_i^a)^{\large\frac{1}{1-a}}[/math] ,
where [math]p_i[/math] = the proportional abundance of species [math]i[/math] in the sample and [math]a[/math] = the order in which the index is dependent of rare species. For very large positive values of [math]a\lt math\gt the Hill number takes into account only the most abundant species, whereas for very large negative values the Hill number takes in account only the rarest species. The most common Hill numbers are \lt math\gt H_0 = \, S [/math],
[math]H_1 = \exp{H'} [/math] (the limit of [math]H_a[/math] for [math]a \to 1[/math] corresponds to the exponential of the Shannon-Wiener diversity index, see appendix A2),
[math]H_2 =\Large\frac{1}{\gamma}[/math] (the reciprocal of Simpson’s [math]\gamma\, [/math]) .
If all species are represented in equal numbers in the sample [math]H_0=H_1=H_2=S[/math].
Taxonomic indices
If two data-sets have identical numbers of species and equivalent patterns of species abundance, but differ in the diversity of taxa to which the species belong, it seems intuitively appropriate that the most taxonomically varied data-set is the more diverse. As long as the phylogeny of the data-set of interest is reasonably well resolved, measures of taxonomic diversity are possible.
- Clarke and Warwick’s taxonomic distinctness index[14] which describes the average taxonomic distance – simply the “path length” between two randomly chosen organisms through the phylogeny of all the species in a data-set – has different forms: taxonomic diversity and taxonomic distinctness.
• Taxonomic diversity ([math]\Delta[/math]) reflects the average taxonomic distance between any two organisms, chosen at random from a sample. The distance can be seen as the length of the path connecting these two organisms through a phylogenetic tree or a Linnean classification[14]. This index includes aspects of taxonomic relatedness and evenness,
[math]\Delta = \Large\frac{ \sum\sum_{i\lt j} \, \omega_{ij} \, n_i n_j}{N(N-1)/2} [/math],
where [math]n_i=n p_i[/math] denotes the abundance of the [math]i[/math]-th species in the sample ([math]\sum_{i=1}^S n_i =N[/math] = the number of individuals in the sample) and [math]\omega_{ij}[/math] is the 'distinctness weight' given to the path length (number of steps) linking species [math]i[/math] and [math]j[/math] in the hierarchical classification. (The path length for two individuals of the same species is zero).
• Taxonomic distinctness ([math]\Delta^*[/math]) is the average path length between two randomly chosen but taxonomically different organisms. This measure is measure of pure taxonomic relatedness,
[math]\Delta^* = \Large\frac{ \sum\sum_{i\lt j} \, \omega_{ij} n_i n_j}{\sum\sum_{i\lt j} \, n_i n_j} [/math].
• When only presence/absence data is considered, both [math]\Delta[/math] and [math]\Delta^*[/math] converge to the same statistic [math]\Delta^+[/math], which can be seen as the average taxonomic path length between any two randomly chosen species[15],
[math]\Delta^+= \Large\frac{\sum\sum_{i\lt j} \, \omega_{ij}}{S(S-1)/2}[/math].
Functional diversity
The positive relationship between ecosystem functioning and species richness is often attributed to the greater number of functional groups found in richer assemblages. Petchey and Gaston [16] proposed a method for quantifying functional diversity. It is based on total branch length of a dendrogram, which is constructed from species trait values. One important consideration is that only those traits linked to the ecosystem process of interest are used. Thus a study focusing on bird-mediated seed dispersal would exclude traits such as plumage color that are not related to this function, but traits such as beak size and shape should be included. With standard clustering algorithms a dendrogram is then constructed. For example, a community with five species with different traits will have a higher functional diversity than a community of equal richness but where the species are functional similar.
Species-Abundance distributions[17]
Nearly all diversity and evenness indices are based on the relative abundance of species, thus on estimates of [math]p_i[/math] in which [math]p_i = n_i / N [/math], with [math]n_i[/math] the abundance of the [math]i[/math]-th species in the sample and [math]N = \sum _{i = 1}^S \, n_i[/math] with [math]S[/math] the total number of species in the sample.
When recording the abundance of different species in a sample, it is invariably found that some species are rare, whereas others are more abundant. This feature of ecological communities is found independently of the taxonomic group or the area investigated. An important goal of ecology is to describe these consistent patterns in different communities, and explain them in terms of interactions with the biotic and abiotic environment.
Different investigators have visualized the species-abundance distribution in different ways (Fig. 3).
1. The rank/abundance plot is one of the best known and most informative method. In this plot species are ranked in sequence from most to least abundant along the horizontal (or [math]x[/math]) axis. Their abundances are typically displayed in a log10 format on the [math]y[/math] axis, so that species whose abundances span several orders of magnitude can be easily accommodated on the same graph. In addition, proportional and or percentage abundances are often used.
2. The [math]k[/math]-dominance plot shows the cumulative percentage (the percentage of the [math]k[/math]-th most dominant plus all more dominant species) in relation to species ([math]k[/math]) rank or log species ([math]k[/math]) rank.
3. The Lorenzen curve is based on the [math]k[/math]-dominance plot but the species rank [math]k[/math] is transformed to [math] (k/S) \times 100[/math] to facilitate comparison between communities with different numbers of species.
4. The collector’s curve addresses a different problem. When the sampling effort is increased, and thus the number of individuals [math]N[/math] caught, new species will appear in the collection. A collector’s curve expresses the number of species as a function of the number of specimens caught. As more specimens are caught, a collector’s curve can reach an asymptotic value. However, this hardly does occur in practice due to the vague boundaries of ecological communities: as the sampling effort increases, the number of different patches increases as well.
5. The species-abundance distribution plots the number of species that are represented by [math]1,2, … , n [/math] individuals against the corresponding abundance. This plot can only be drawn if the collection is large and contains many species. The species are generally grouped in logarithmic density classes.
Species-Abundance models[2]
Besides the log-series and log-normal models, also other models have been developed to describe species abundance data (Fig. 4). These models are based on species abundance observed in diverse ecosystems.
The niche preemption model or the geometric model
It assumes that a species preempts a fraction [math]k[/math] of a limiting resource, a second species the same fraction [math]k[/math] of the remainder and so on. If the abundances are proportional to their share of the resource, the ranked abundances list is given by geometric series (see appendix A3):
[math]\Large\frac{n_i}{N}\normalsize=\Large\frac{k(1-k)^{(i-1)}}{1-(1-k)^S}[/math],
where [math]S[/math] is the number of the species in the community. For large values of [math]S[/math] this distribution depends only on the parameter [math]k[/math]. In this case the Shannon-Wiener index is given by [math]H' \approx ((k-1)/k) \ln(1-k) - \ln(k)[/math]. For small values of [math]k[/math] the index is large (high biodiversity) and for values of [math]k[/math] close to 1 the index is close to zero (low biodiversity).
The geometric model gives a straight line on a plot of log abundance against rank (species sequence). It is not very often found in nature, only in early successional stages or in species poor environments[17].
The broken stick model or the negative exponential distribution
In this model a limiting resource is compared with a stick, broken in [math]S[/math] parts at [math]S-1[/math] randomly located points. The length of the parts is taken as representative for the density of the [math]S[/math] species subdividing the limiting resource. If the species are ranked according to abundance, the expected abundance [math]n_i[/math] of species [math]i[/math] is given by[18]:
[math]\Large\frac{n_i}{N}\normalsize= \Large\frac{1}{S}\normalsize \sum_{k = i}^S \frac{1}{k} [/math].
This distribution satisfies the condition [math]N = \sum_{i=1}^S n_i [/math]. The dependence on the single parameter [math]S[/math] is weak for large values of [math]S[/math]. For large values of [math]S[/math] the Shannon-Wiener index is close to [math]H' \approx ln(S)[/math].
The negative exponential distribution is not often found in nature; it describes a too even distribution of individuals over species to be a good representation of natural communities[17].
Appendix A1
The Shannon-Wiener diversity index is a measure of the information (in fact, the 'lack of information', or 'uncertainty' or 'information entropy') represented by a sample, where information is defined as the minimum length of a string of digits necessary to describe the sample. The minimum length of a string of digits to describe a number is proportional to the logarithm of this number. All the ways in which [math]N[/math] individuals can be distributed in numbers [math]n_1, n_2, …, n_S[/math] for the species [math]1, 2, …., S[/math] are equivalent and thus provide no information. With this definition, a measure of the information uncertainty in a large sample is given by the logarithm of the number [math]P[/math] of all different permutations of individuals that give the same distribution of individuals over species. If [math]P[/math] is large, the sample can be ordered in many distinct equivalent ways and thus conveys few information (= high information entropy = high diversity). This is the case, for example, if all [math]N[/math] individuals in a sample belong to different species. The number of distinct permutations is then equal to [math]P=N![/math] (the first individual in an ordered sample can be chosen in [math]N[/math] ways, the second in [math]N-1[/math] ways and so on). If there are [math]n_1[/math] individuals of species 1, [math]n_2[/math] individuals of species 2, and so on, then the number of equivalent distinct permutations is [math]P = N!/(n_1! \times n_2! \times . . . . \times n_S!)[/math]. Taking the logarithm gives [math]N \times[/math] the Brillouin index [math]H[/math]. Assuming that the numbers [math]N, n_1, n_2, ….[/math] are very large, one can approximate [math]\ln(n_i!) \approx n_i\, \ln(n_i) [/math]. This gives [math]\ln(P) \approx N \, \ln(N) – n_1 \, \ln(n_1) – n_2\, \ln(n_2) - ….. n_S \, \ln(n_S) [/math]. For large representative samples the probability of occurrence of species [math]i[/math] is given by [math]p_i=n_i/N[/math]. We further have [math]\sum_{i=1}^{S} p_i=1[/math]. Substitution gives [math]\ln(P) \approx -N \sum_{i=1}^{S} p_i \, \ln(p_i)[/math], which is [math]N \times[/math] the Shannon-Wiener index [math]H'[/math]. Division by [math]N[/math] makes the index independent of the sample size.
Another interpretation of the Shannon-Wiener index is: the mean number of digits required for describing the probability [math]p_i[/math] to find [math]n_i[/math] individuals of species [math]i[/math] in the sample of [math]N[/math] individuals. The number of digits for describing the probability [math]p_i[/math] is proportional to [math]-\ln(p_i)[/math] (the rarer the species, the smaller [math]p_i[/math] and the more digits are needed). The mean is obtained by taking the weighted sum of the number of digits: [math]H'= - \sum_{i=1}^S p_i \ln(p_i)[/math].
Appendix A2
Take [math]a=1+\epsilon[/math] and [math]\epsilon \to 0[/math], then [math]p_i^a \to p_i+\epsilon \large\frac{d}{d \epsilon} p_i^{1+\epsilon}\normalsize \approx p_i + \epsilon p_i \ln p_i[/math]. Because [math]\sum_{i=1}^S p_i = 1[/math], we have
[math]H_1 = \lim_{\epsilon \to 0} (1 + \epsilon \sum_{i=1}^S p_i \ln p_i)^{-1/\epsilon} = \exp(-\sum_{i=1}^S p_i \ln p_i)[/math].
Appendix A3
According to the assumptions underlying the model, the numbers [math]\, n_1, n_2, …., n_S \, [/math] of species [math]\, 1, 2, …., S \,[/math] are
[math]n_1=Ck, \; n_2= Ck(1-k), \; n_3=Ck(1-k-k(1-k))=Ck(1-k)^2, …., \; n_S=Ck(1-k)^{(S-1)} [/math].
We have [math]N = \sum_{i=1}^S n_i = Ck\sum_{i=1}^S (1-k)^{(i-1)} = C(1-(1-k)^S) [/math], hence [math]C=\Large\frac{N}{1-(1-k)^S}[/math].
See also
Further reading
- Magurran, A. E. 2004. Measuring biological diversity, Blackwell Publishing: Oxford, UK. 256 p
References
- ↑ [\http://en.wikipedia.org/wiki/Biodiversity#Measurement_of_biodiversity Wikipedia article Measurement of biodiversity
- ↑ 2.0 2.1 Magurran, A. E. 2004. Measuring biological diversity, Blackwell Publishing: Oxford, UK. 256 p
- ↑ Clifford H.T. and Stephenson W. 1975. An introduction to numerical classification. London: Academic Express.
- ↑ Whittaker R.H. 1977. Evolution of species diversity in land communities. Evolutionary Biol. 10: 1-67
- ↑ Fisher, R. A., Corbet, A. S. and Williams, C. B. 1943. The relation between the number of species and the number of individuals in a random sample of an animal population. Journal of Animal Ecology 12: 42-58
- ↑ Preston, F.W. 1948. The commonness and rarity of species. Ecology 29: 254–283
- ↑ 7.0 7.1 Magurran, A.E. and Henderson, P.A. 2003. Explaining the excess of rare species in natural species abundance distributions. Nature 422: 714–716
- ↑ Shannon C. E. and Weaver W. 1949. The mathematical theory of communication. Urbana, IL: University of Illinois Press.
- ↑ 9.0 9.1 Pielou E.C. 1975. Ecological diversity. New York: Wiley Interscience.
- ↑ Pielou E.C. 1969. An introduction to mathematical ecology. New York: Wiley.
- ↑ Simpson E.H. 1949. Measurement of diversity. Nature 163: 688.
- ↑ Pielou, E.C. 1966. The measurement of diversity in different types of biological collection. Journal of Theoretical Biology 13: 131–144
- ↑ Hill, M.O. 1973. Diversity and evenness: a unifying notation and its consequences. Ecology 54: 427–473
- ↑ 14.0 14.1 Warwick R.M. and Clarke K.R. 2001. Practical measures of marine biodiversity based on relateness of species. Oceanogr. Mar. Biol. Ann. Rev. 39: 207-231
- ↑ Clarke K.R. and Warwick R.M. 1998. A taxonomic distinctness index and its statistical properties Journal of Applied Ecology 35 (4): 523-531
- ↑ Petchey O.L. and Gaston K.J. 2002. Functional diversity (FD), species richness and community composition. Ecology letters Vol. 5 (3): 402-411
- ↑ 17.0 17.1 17.2 Heip, C.H.R., Herman, P.M.J. and Soetaert, K. 1998. Indices de diversité et régularité. [Indices of diversity and evenness]. Océanis (Doc. Océanogr.) 24(4): 67-87
- ↑ McArthur, R.H. 1957. On the relative abundance of bird species. Proc. Natl. Acad. Sci. USA 43: 293-295
Please note that others may also have edited the contents of this article.
|







