Difference between revisions of "Salt wedge estuaries"

From Coastal Wiki
Jump to: navigation, search
 
(6 intermediate revisions by the same user not shown)
Line 5: Line 5:
 
==Introduction==
 
==Introduction==
  
−
In estuaries where tidal motion is very weak or absent, seawater intrudes in the form of a wedge along the bottom, as a consequence of the higher density of seawater compared to fresh water. The intrusion length depends essentially on two parameters: river flow velocity <math>v</math> and water depth <math>h</math>.  This article deals with the hydrodynamic balances that determine the salt wedge, illustrated by a model for a prismatic estuary (uniform depth and width). We follow the derivation first given by Schijf and Schönfeld in 1953 <ref>Schijf, J.B., Schönfeld, J.C. (1953) Theoretical considerations on the motion of salt and fresh water. Proceedings of the 5th I.A.H.R. Congress, 321–333</ref>.
+
In estuaries where tidal motion is very weak or absent, seawater intrudes in the form of a wedge along the bottom, as a consequence of the higher [[Seawater density|density of seawater]] compared to fresh water. The intrusion length depends essentially on two parameters: river flow velocity <math>v</math> and water depth <math>h</math>.  This article deals with the hydrodynamic balances that determine the salt wedge, illustrated by a model for a prismatic estuary (uniform depth and width). We follow the derivation first given by Schijf and Schönfeld in 1953 <ref>Schijf, J.B., Schönfeld, J.C. 1953. Theoretical considerations on the motion of salt and fresh water. Proceedings of the 5th I.A.H.R. Congress, 321–333</ref>.
  
−
In most estuaries, seawater intrusion is strongly influenced by tidal motion (see [[Estuarine circulation]]). Even in microtidal estuaries this influence is often significant <ref>Geyer, R.W. and Farmer, D.H. (1989) Tide-induced variation of the dynamics of a salt wedge estuary. J. Phys. Oceanography 19: 1060-1072</ref>. In some cases, especially in the Mediterranean Sea, tides are so small that their influence on seawater intrusion is minor. This article focuses on such situations; we assume that the salt wedge is not significally altered during the slight tidal motion up and down the estuary.   
+
In most estuaries, seawater intrusion is strongly influenced by tidal motion (see [[Estuarine circulation]]). Even in microtidal estuaries this influence is often significant <ref>Geyer, R.W. and Farmer, D.H. 1989. Tide-induced variation of the dynamics of a salt wedge estuary. J. Phys. Oceanography 19: 1060-1072</ref>. In some cases, especially in the Mediterranean Sea, tides are so small that their influence on seawater intrusion is minor. This article focuses on such situations; we assume that the salt wedge is not significally altered during the slight tidal motion up and down the estuary.   
  
−
==Hydrodynamic balance==
+
==Seawater intrusion process==
  
−
[[Image:SaltWedge.jpg|thumb|500px|right|Figure 1: Salt wedge in a prismatic estuary. The sea boundary is situated at <math>x</math>=0. The shape of the salt wedge shown in the figure corresponds to the theoretical curve (solution of Eq. (5)) for 8 m water depth, river flow velocity 0.3 m/s, salt layer density 1020 kg/m3  (internal river Froude number <math>F_i</math>=0.24) and interfacial shear stress coefficient <math>C_i</math>=0.0002. ]]
+
[[Image:SaltWedgeZero.jpg|thumb|500px|right|Figure 1: Longitudinal section of river with a fictitious corrugated sloping bottom. The sea boundary is at <math>x=0</math>. The river discharge is very small; the upper boundary of the salt wedge is almost horizontal. The salt intrusion length <math>L</math> corresponds to the location where the level of the river bed equals the sea level.]]
  
−
Here we introduce a simple two-layer model for describing seawater intrusion in a microtidal prismatic (uniform width and depth) estuary. The salt wedge is represented by a separate layer of thickness <math>h_2</math> along the bottom of the estuary, see figure 1. The total water depth <math>h</math> is the sum of the bottom layer thickness <math>h_2</math> and the upper surface layer thickness <math>h_1</math>. Lateral variations of depth, density (salinity) and velocity are ignored. The velocity is indicated by <math>v</math> and the density by <math>\rho</math>. Subscripts 1 and 2 indicate the surface layer and the bottom layer respectively.
+
First consider the case of a very small river discharge such that the stress it exerts on the salt wedge is not significant. The absence of forces leads to an equilibrium situation where the salt wedge slope is zero. The level of the river bed rises inland; at some point inland, the level is equal to the sea level. Seawater can enter the river that far. The salt intrusion length is determined by the intersection of the sea level with the river bed, see Fig. 1.  
  
−
Seawater intrusion is accelerated by the pressure gradient <math>d p_2 / d x</math> related to the slope of the salt wedge <math>d h_2 / d x</math> and the slope of the overlying fresh water <math>d h_1 / d x</math>,
+
In general, the shear stress exerted by the river on the intruding seawater cannot be neglected. We consider a situation without tide or a very small tide (tidal flow velocities much less than the flow velocity due to river discharge) and constant river discharge. We then have a stationary salt wedge, also called 'arrested salt wedge'. Except for extreme river discharges, the rate at which river water flows over the seawater wedge is not fast enough to produce complete mixing of the water column. However, the river flow velocity is high enough to produce a thin mixing layer. The river water exerts a shear stress on the seawater wedge via this mixing layer. The surface of the seawater wedge is therefore inclined (the pycnocline), such that the hydrostatic force (due to the slopes of the salt wedge and the water surface) balances the shear stress, see Fig. 2. The thin mixing layer is generally turbulent; the shear stress is therefore proportional to the square of the velocity difference over the mixing layer and it is assumed that it can be parameterized as the product of the river flow velocity squared and a shear stress coefficient <math> C_i </math>. In theory, this coefficient should have a certain fixed value, but experimental observations yield various values. 
  
−
<math>\Large \frac{d p_2}{d x} \normalsize = g \rho_2 ( \beta + \Large \frac{d h_2}{d x} \normalsize )+ g \rho_1 \Large \frac{d h_1}{d x} \normalsize , \qquad (1) </math>
+
[[Image:SaltWedgeMod.jpg|thumb|500px|right|Figure 2: Longitudinal section of a salt wedge in a prismatic estuary. The sea boundary is situated at <math>x</math>=0. The shape of the salt wedge shown in the figure corresponds to the theoretical curve (solution of Eq. (1)) for 8 m water depth, river flow velocity 0.3 m/s, salt layer density 1020 kg/m3  (internal river Froude number <math>F_i</math>=0.24) and interfacial shear stress coefficient <math>C_i</math>=0.00025. ]]
  
−
where <math>\rho_1=\rho</math> is the fresh water density, <math>\rho_2=\rho+ \Delta \rho</math> the seawater density and <math>\beta</math> the bottom slope. Other symbols are shown in figure 1. Because of the lower density of fresh water compared to seawater, this pressure gradient generally acts in upstream direction. The acceleration of the salt wedge is balanced by friction at the interface induced by the overlying river flow. The shear stress <math>\tau_i</math> exerted by river flow on the salt wedge can be parameterized as  <math>\tau_i / \rho = C_i v_1^2 </math>, where <math>C_i</math> is the  interfacial shear stress coefficient of order <math>10^{-4}-10^{-3} .</math><ref>Abraham, G., Karelse, M. and Van Os, A.G. (1979) On the magnitude of the interfacial shear stress of subcritical stratified flows in relation with interfacial stability. Hydr. Res. 17: 273-287</ref>
+
The reason is that the ideal situation of a stationary salt wedge hardly occurs in practice. The river discharge varies, the tide is not negligibly small, extra turbulence is caused by a non-uniform river geometry, by waves, wind and shipping. Numerical models can partly quantify these influences, but it is difficult to accurately predict the salt intrusion length.
  
−
The salt wedge intrusion is also influenced by bottom friction. However, in a stationary situation (called “arrested salt wedge”) bottom friction does not play a role because the salt wedge is at rest.
 
  
−
River flow is confined to a progressively thinner layer in downstream direction. The resulting acceleration of river flow creates a gradient in the hydraulic head given by <math>\rho v_1 d v_1 / d x .</math>  The surface layer is further accelerated by the surface pressure gradient
+
==Seawater intrusion length==
  
−
<math>\Large \frac{d p_1}{d x} \normalsize = g \rho_1 ( \beta + \Large \frac{d h_2}{d x} + \frac{d h_1}{d x} \normalsize)  \qquad (2) </math>  
+
If the tide has a significant influence on the seawater intrusion process, an estuarine circulation is generated; this situation is discussed in the article [[Estuarine circulation]]. Here we assume the simpler case that the influence of the tide can be neglected. In the special case that the river geometry can be approached by a prismatic channel (uniform depth and width, no bottom slope). The relative depth of the upper fresh water layer <math>y=h_1/h</math> then satisfies the differential equation (see Appendix)
  
−
and decelerated by the interfacial shear stress <math>\tau_i .</math> The hydrodynamic balance (no acceleration) of the two layers is therefore given by the equations
+
<math> \large\frac{d}{dx} \normalsize  [ -4 y^5 + 5y^4 - 10 F_i^2 y(2-y) ] = 20 \large \frac{C_i F_i^2}{h} \normalsize , \qquad (1) </math>
  
−
<math>\Large \frac{d p_2}{\rho_2 d x} + \frac{\tau_i}{\rho h_2} \normalsize = 0;  \; \Large \frac{d p_1}{\rho_1 d x} \normalsize  = -  v_1 \; \Large \frac{d v_1}{d x}  - \frac{\tau_i}{\rho h_1} \normalsize . \qquad (3)</math>
+
where the internal Froude number <math>F_i</math> is given by
  
−
==Salt wedge model for a prismatic estuary==
+
<math>F_i = \large \frac{Q}{hb} \normalsize [ \epsilon g h]^{-1/2} , \qquad (2)</math>
  
−
In a prismatic estuary the depth <math>h</math> and width <math>b</math> do not vary along the channel axis. By subtracting the two layer equations the salt wedge slope <math>d h_2 / d x</math> and the bottom slope <math>\beta</math> are eliminated. By assuming that the bottom slope is not much larger than the salt wedge slope, we may approximate <math>h_2 \approx h-h_1 .</math> The velocity in the upper layer <math>v_1</math> can be eliminated from the equations by using the condition of continuity of river discharge per unit width,
+
<math>Q</math>= river discharge, <math>h</math>= river depth, <math>b</math>= river width and <math>\epsilon=\large \frac{\Delta \rho}{\rho} \normalsize </math>= relative density difference of seawater and river water. The differential equation (1) is easily integrated if conditions at both boundaries of the salt wedge are known.  
  
−
<math>h_1 v_1 = h v = \Large \frac{Q}{b} \normalsize, \qquad (4) </math>  
+
The conditions at the tip of the salt wedge is obvious: <math>y=1</math> at <math>x=L </math>.
  
−
where <math>Q</math> is the river discharge. These manipulations lead to an ordinary nonlinear differential equation for the variable <math>y=h_1 / h ,</math>
+
The condition at the sea boundary is more subtle. The upper layer depth cannot be zero because no fresh water could be discharged to the sea. When during the process of seawater intrusion the depth of the upper layer at the sea boundary decreases, the outflow velocity <math>v_1</math> increases. However, the intrusion process stops when the outflow velocity equals the critical velocity <math>v_c</math>. This is because a further upward shift of the interface boundary at sea cannot propagate upstream into the river. The critical velocity for upstream propagation of a perturbation at the interface is given by
  
 +
<math>v_c=[\large \frac{\Delta \rho}{\rho} \normalsize g h_1]^{1/2} . \qquad (3) </math>
  
−
<math> (y^3-F_i^2)(1-y) dy = \Large \frac{C_i F_i^2}{h} \normalsize dx , \qquad (5) </math>
+
Substitution in  Eq. (2) gives <math>F_i = \large \frac{h_1 v_c}{h} \normalsize [\large \frac{\Delta \rho}{\rho} \normalsize g h]^{-1/2} = \large(\frac{h_1}{h})^{3/2}\normalsize = y(0)^{3/2}</math>,
  
 +
from which it follows that the boundary conditions at the sea boundary <math>x=0</math> is given by  <math>y(0) =  F_i^{2/3} .  \qquad (4)</math>
  
−
where  <math>F_i = v [\Large \frac{\Delta \rho}{\rho} \normalsize g h]^{-1/2} = \Large \frac{Q}{hb} \normalsize [\Large \frac{\Delta \rho}{\rho} \normalsize g h]^{-1/2} </math> is the internal river Froude number.
+
Integration of the differential equation with the two boundary conditions gives the length <math>L</math> at constant river discharge:
  
 +
<math>L = \Large \frac{h}{20 C_i} \normalsize (-10+15F_i^{2/3}-6F_i^{4/3}+F_i^{-2}) . \qquad (5)</math>
  
−
This equation can be easily integrated if conditions at both boundaries of the salt wedge are known.  
+
In this expression, the salt intrusion length is inversely proportional to the interfacial shear stress coefficient <math>C_i</math>. The value of this coefficient cannot be determined via the model and must therefore be determined independently.  
  
−
The conditions at the tip of the salt wedge is obvious: <math>y=1</math> at <math>x=L .</math>.  
+
The dimensionless salt wedge length <math>C_i L / h</math> as a function of the internal river Froude number <math>F_i</math> is shown in Fig. 3. The condition at the sea boundary plays a crucial role for the salt wedge length. The depth of the river outflow layer <math>h_1(0)</math> is proportional to the river discharge at the power 2/3, according to the equations (2) and (4). Therefore the depth of the salt wedge layer at the mouth, <math>h_2(0)</math>, becomes very small for high river discharge.  
  
−
The condition at the sea boundary is more subtle. When during the process of seawater intrusion the depth of the upper layer at the sea boundary decreases, the outflow velocity <math>v_1</math> increases. However, the intrusion process stops when the outflow velocity equals the critical velocity <math>v_c</math> at which an upward shift of the interface cannot propagate upstream. The critical velocity for upstream propagation of a perturbation at the interface is given by
+
Integration of Eq. (1) also gives the shape of the seawater wedge, shown in Fig. 2 for particular values of river depth, river discharge and shear stress coefficient <math> C_i </math>.
  
−
<math>v_c=[\Large \frac{\Delta \rho}{\rho} \normalsize g h_1]^{1/2} . \qquad (6) </math>
+
Generally, the analytical model cannot be used for predicting salt intrusion at low river discharge. This is an important limitation, because precisely this information is often most relevant in practice. The problem is that there is no analytical solution to the equations in the case of a sloping river bed. At low river runoff, the seawater intrudes thus far that the influence of the bottom slope cannot be neglected. In that case, the equations describing the seawater intrusion must be solved numerically. For rivers with a strongly sloping river bed, a first estimate of the salt intrusion length at low river discharge is obtained by the intersection of the seawater level with the river bottom, as shown in Fig. 1.
  
−
[[Image:SaltWedgeLength.jpg|thumb|500px|right|Figure 2: Dimensionless salt wedge length <math>C_i L / h</math> according to Eq. (7) for a prismatic estuary and observed salt wedge lengths in the Rhône and Ebro estuaries at different discharges (corresponding to different internal river Froude numbers <math>F_i</math>). The following values are used: <math>C_i</math>=0.0002, depth <math>h</math> is 8 m for the Rhône and  5 m for the Ebro, width <math>b</math> is 300 m for the Rhône and 180 m for the Ebro. Mean river discharges for the Rhône and the Ebro are 1500 and 400 m3/s, respectively. Data are from <ref>Ibanez, C., Pont, P. and Prat, N. (1997) Characterization of the Ebre and Rhone estuaries: A basis for defining and classifying salt-wedge estuaries. Limnol. Oceanograph. 42: 89-10 </ref>. No correction has been made for the variation of water depth with discharge. Such a correction would bring the observed salt wedge lengths somewhat closer to the theoretical curve. ]]
+
Additional mixing of river water and sea water can occur as a consequence of local river contractions, sharp river bends and high bottom sills. In these cases too, the analytical solution is less reliable and it is better to use a numerical model to determine the seawater intrusion.
  
−
Because <math>h_1 v_c = hv</math>, the boundary conditions at <math>x=0</math> is given by <math>y=F_i^{2/3} . </math> Integration of the differential equation with these two boundary conditions gives the shape of the stationary salt wedge (see figure 1) and the length <math>L</math> at constant river discharge:
 
  
−
<math>L = \Large \frac{20h}{C_i} \normalsize (-10+15F_i^{2/3}-6F_i^{4/3}+F_i^{-2}) . \qquad (7)</math>
+
==Comparison with observations==
 +
 
 +
[[File:WedgeLengthObsMod6.jpg|thumb|500px|right|Figure 3: Dimensionless salt wedge length <math>C_i L / h</math> according to Eq. (5) for a prismatic estuary and observed salt wedge lengths in the Rhône, Ebro <ref name=I>Ibanez, C., Pont, D. and Prat, N. 1997. Characterization of the Ebre and Rhone estuaries: A basis for defining and classifying salt-wedge estuaries. Limnol. Oceanogr. 42:
 +
89–101</ref>, the Mississippi <ref name=RM>Rattray, M. Jr and Mitsuda, E. 1974. Theoretical analysis and conditions in a salt wedge. Estuarine and Coastal Marine Science 2: 375-394</ref>, Magdalena<ref name=A22>Arevalo, F.M., Alvarez-Silva, O., Caceres-Euse, A. and Cardona, Y. 2022. Mixing mechanisms at the strongly-stratified Magdalena River’s estuary and plume. Estuarine, Coastal and Shelf Science 277, 108077</ref> and Neretva<ref name=K21>Krvavica, N., Gotovac, H. and Loncar, G. 2021. Salt-wedge dynamics in microtidal Neretva River estuary. Regional Studies in Marine Science 43, 101713</ref> estuaries at different discharges (corresponding to different internal river Froude numbers <math>F_i</math>). For all estuaries the same value is used for the interfacial shear stress coefficient, <math>C_i</math>=0.00025. Other parameters are indicated in Table 1.]]
 +
 
 +
The Rhône (France) and the Ebro (Spain) are examples of estuaries with almost no tidal motion (both situated on the Mediterranean coast, tidal amplitude in the order of 0.1 m on average). The tidal amplitude for the Mississippi at the US Gulf coast is in the order of 0.25 m on average; the tidal current velocities are small, but not much smaller than the river flow velocities for the lowest discharges considered in the comparison. The Magdalena (Colombia) discharges into the Caribbean Sea with a predominantly diurnal, mixed microtidal regime. The tidal range of 0.13 m to 0.40 m produces small tidal velocities that shift the salt water front over a distance of about 300 m<ref>Ospino, S., Restrepo, J.C., Otero, L., Pierini, J. and Alvarez-Silva, O. 2018. Saltwater intrusion into a river with high fluvial discharge: a microtidal estuary of the Magdalena River, Colombia. J. Coast Res. 34: 1273–1288</ref>. 
  
−
The dimensionless salt wedge length <math>C_i L / h</math> as a function of the internal river Froude number <math>F_i</math> is shown in figure 2. The condition at the sea boundary plays a crucial role for the salt wedge length. The depth of the river outflow layer is proportional to the river discharge at the power 2/3. Therefore the depth of the salt wedge layer becomes very small for high river discharge.  
+
Figure 3 shows the observed dimensionless salt wedge lengths <math>C_i L / h</math> in these estuaries for different internal river Froude numbers <math>F_i</math>. The observed lengths are compared with the theoretical result for a prismatic estuary (Eq. (5)), where the same interfacial shear stress coefficient is used for all the estuaries. For very small river flow the model lengths are much larger than the observed intrusion lengths. This is due in particular to the presence of high sills in the upstream part of the Rhône estuary (at 35 km from the mouth) and Ebro estuary (at 32 km from the mouth). Other less pronounced sills situated downstream also tend to arrest the salt wedge for a certain range of river discharges; the salt wedge length <math>L</math> therefore does not increase continuously as a function of <math>F_i</math>, as would be the case for a true prismatic canal. The reasonable correspondence between observed and computed salt intrusion lengths for low-to-mean river discharges does not imply that the value of the interfacial shear stress coefficient, <math>C_i=0.00025</math>, should hold in general. In the present comparison this coefficient includes the effect of several factors by which the analytical model deviates from the real estuaries, such as deviations from the prismatic geometry (bed slope, sills, etc.) and tidal influence. 
 +
 
 +
 
 +
==Appendix 1: Analytical model for a prismatic estuary ==
 +
 
 +
The following is a simple two-layer description of seawater intrusion in a microtidal prismatic (uniform width and depth) estuary. The salt wedge is represented by a separate layer of thickness <math>h_2</math> along the bottom of the estuary, see figure 2. The total water depth <math>h</math> is the sum of the bottom layer thickness <math>h_2</math> and the upper surface layer thickness <math>h_1</math>. Lateral variations of depth, density (salinity) and velocity are ignored. The velocity is indicated by <math>v</math> and the density by <math>\rho</math>. Subscripts 1 and 2 indicate the surface layer and the bottom layer respectively.
 +
 
 +
The pressure gradient <math>d p_2 / d x</math> in the lower layer is related to the slope of the salt wedge (relative to a horizontal reference plane) and to the pressure gradient exerted by the overlying fresh water,
 +
 
 +
<math>\Large \frac{d p_2}{d x} \normalsize = g \rho_2 ( \beta + \Large \frac{d h_2}{d x} \normalsize )+ g \rho_1 \Large \frac{d h_1}{d x} \normalsize , \qquad (A1) </math>
 +
 
 +
where <math>\rho_1=\rho</math> is the fresh water density, <math>\rho_2=\rho+ \Delta \rho</math> the seawater density and <math>\beta</math> the bottom slope. Other symbols are shown in Fig. 2. Because of the lower density of fresh water compared to seawater, this pressure gradient generally acts in upstream direction. A counteracting pressure gradient is produced by friction at the interface (pycnocline) induced by the overlying river flow. The shear stress <math>\tau_i</math> exerted by river flow on the salt wedge is parameterized as  <math>\tau_i / \rho = C_i v_1^2 </math>, where <math>C_i</math> is the  interfacial shear stress coefficient of order <math>10^{-4}-10^{-3} .</math><ref>Abraham, G., Karelse, M. and Van Os, A.G. 1979. On the magnitude of the interfacial shear stress of subcritical stratified flows in relation with interfacial stability. Hydr. Res. 17: 273-287</ref>
 +
 
 +
The salt wedge intrusion is also influenced by bottom friction. However, in a stationary situation bottom friction does not play a role because the salt wedge is at rest.
 +
 
 +
River flow is confined to the upper layer which becomes thinner in downstream direction. The resulting spatial acceleration of river flow creates a gradient in the hydraulic head given by <math>\rho v_1 d v_1 / d x .</math>  The surface layer is further subjected to a pressure gradient related to the water surface slope (relative to a horizontal reference plane),
 +
 
 +
<math>\Large \frac{d p_1}{d x} \normalsize = g \rho_1 ( \beta + \Large \frac{d h_2}{d x} + \frac{d h_1}{d x} \normalsize)  ,  \qquad (A2) </math>
 +
 
 +
and to the interfacial shear stress <math>\tau_i .</math> The stationary hydrodynamic balance of the two layers is therefore given by the equations
 +
 
 +
<math>\Large \frac{d p_2}{\rho_2 d x} + \frac{\tau_i}{\rho h_2} \normalsize = 0;  \; \Large \frac{d p_1}{\rho_1 d x} \normalsize  +  v_1 \; \Large \frac{d v_1}{d x}  - \frac{\tau_i}{\rho h_1} \normalsize = 0 . \qquad (A3)</math>
 +
 
 +
In a prismatic estuary the depth <math>h</math> and width <math>b</math> do not vary along the channel axis. By subtracting the two layer equations the salt wedge slope <math>d h_2 / d x</math>  and the bottom slope <math>\beta</math> are eliminated. By assuming that the bottom slope is not much larger than the surface slope (water depth <math>h</math> approximately constant), we can substitute <math>h_2 \approx h-h_1</math>. The velocity in the upper layer <math>v_1</math> can be eliminated from the equations by using the condition of continuity of river discharge per unit width,
 +
 
 +
<math>h_1 v_1 = h v = Q / b, \qquad (A4) </math>
 +
 
 +
where <math>Q</math> is the river discharge. These manipulations lead to the ordinary nonlinear differential equation for the variable <math>y=h_1 / h</math>,
 +
 
 +
<math>  (y^3-F_i^2)(1-y) \large\frac{dy}{dx} \normalsize = \large \frac{C_i F_i^2}{h} \normalsize , \qquad (A5) </math> 
 +
 
 +
with <math>F_i = \large \frac{Q}{hb} [ \frac{gh \Delta \rho}{ \rho}]^{-1/2} \normalsize  .</math>
 +
 
 +
This is equivalent to Eq. (1) indicated above.
 +
 
 +
 
 +
==Appendix 2: Parameters of a few salt wedge estuaries==
 +
 
 +
{|  style="border-collapse:collapse;background:ivory; font-size: 14px " cellpadding=5px align=center width=70%
 +
|+ Table 1. Data of observed salt wedge lengths for the Rhône (France)<ref name=I/> and Ebro (Spain)<ref name=I/>, the Mississippi (US)<ref name=RM/>, Magdalena (Colombia)<ref name=A22/> and Neretva (Croatia)<ref name=K21/> estuaries. The indicated depths are not mean depths, but the smallest depths along the thalweg below the salt wedge taking into account natural sills. 
 +
|- style="font-weight:bold; text-align:center; background:lightblue"
 +
! width="20% style=" border:1px solid blue;"| Estuary
 +
! width="10% style=" border:1px solid bleu;"| depth [m]
 +
! width="10% style=" border:1px solid blue;"| cross section [m<sup>2</sup>]
 +
! width="10% style=" border:1px solid blue;"| river discharge [m<sup>3</sup>/s]
 +
! width="10% style=" border:1px solid blue;"| observed salt wedge intrusion length <math>L</math> [km]
 +
! width="10% style=" border:1px solid blue;"| <math>L</math> from Eq. (5), <math>C_i=2.5 \, 10^{-4}</math>
 +
|-
 +
| style="border:2px solid lightblue;text-align:center" rowspan="4| Rhône
 +
| style="border:2px solid lightblue;text-align:center"| 8
 +
| style="border:2px solid lightblue;text-align:center"| 2500
 +
| style="border:2px solid lightblue;text-align:center"| 500
 +
| style="border:2px solid lightblue;text-align:center"| 35
 +
| style="border:2px solid lightblue;text-align:center"| 53
 +
|-
 +
| style="border:2px solid lightblue;text-align:center"| 8
 +
| style="border:2px solid lightblue;text-align:center"| 2500
 +
| style="border:2px solid lightblue;text-align:center"| 600
 +
| style="border:2px solid lightblue;text-align:center"| 28
 +
| style="border:2px solid lightblue;text-align:center"| 34
 +
|-
 +
| style="border:2px solid lightblue;text-align:center"| 8
 +
| style="border:2px solid lightblue;text-align:center"| 3000
 +
| style="border:2px solid lightblue;text-align:center"| 850
 +
| style="border:2px solid lightblue;text-align:center"| 20
 +
| style="border:2px solid lightblue;text-align:center"| 23
 +
|-
 +
| style="border:2px solid lightblue;text-align:center"| 8
 +
| style="border:2px solid lightblue;text-align:center"| 3000
 +
| style="border:2px solid lightblue;text-align:center"| 1200
 +
| style="border:2px solid lightblue;text-align:center"| 9
 +
| style="border:2px solid lightblue;text-align:center"| 9
 +
|-
 +
| style="border:2px solid lightblue;text-align:center" rowspan="3| Ebro
 +
| style="border:2px solid lightblue;text-align:center"| 5.5
 +
| style="border:2px solid lightblue;text-align:center"| 1000
 +
| style="border:2px solid lightblue;text-align:center"| 80
 +
| style="border:2px solid lightblue;text-align:center"| 32
 +
| style="border:2px solid lightblue;text-align:center"| 177
 +
|-
 +
| style="border:2px solid lightblue;text-align:center"| 5.5
 +
| style="border:2px solid lightblue;text-align:center"| 1000
 +
| style="border:2px solid lightblue;text-align:center"| 250
 +
| style="border:2px solid lightblue;text-align:center"| 18
 +
| style="border:2px solid lightblue;text-align:center"| 13
 +
|-
 +
| style="border:2px solid lightblue;text-align:center"| 5.5
 +
| style="border:2px solid lightblue;text-align:center"| 1000
 +
| style="border:2px solid lightblue;text-align:center"| 400
 +
| style="border:2px solid lightblue;text-align:center"| 5
 +
| style="border:2px solid lightblue;text-align:center"| 3
 +
|-
 +
| style="border:2px solid lightblue;text-align:center" rowspan="2| Mississippi main channel
 +
| style="border:2px solid lightblue;text-align:center"| 18
 +
| style="border:2px solid lightblue;text-align:center"| 14220
 +
| style="border:2px solid lightblue;text-align:center"| 2830
 +
| style="border:2px solid lightblue;text-align:center"| 220
 +
| style="border:2px solid lightblue;text-align:center"| 296
 +
|-
 +
| style="border:2px solid lightblue;text-align:center"| 18
 +
| style="border:2px solid lightblue;text-align:center"| 14220
 +
| style="border:2px solid lightblue;text-align:center"| 4250
 +
| style="border:2px solid lightblue;text-align:center"| 140
 +
| style="border:2px solid lightblue;text-align:center"| 120
 +
|-
 +
| style="border:2px solid lightblue;text-align:center" rowspan="3| Mississppi southwest pass
 +
| style="border:2px solid lightblue;text-align:center"| 14
 +
| style="border:2px solid lightblue;text-align:center"| 6440
 +
| style="border:2px solid lightblue;text-align:center"| 2550
 +
| style="border:2px solid lightblue;text-align:center"| 32
 +
| style="border:2px solid lightblue;text-align:center"| 35
 +
|-
 +
| style="border:2px solid lightblue;text-align:center"| 14
 +
| style="border:2px solid lightblue;text-align:center"| 6440
 +
| style="border:2px solid lightblue;text-align:center"| 2830
 +
| style="border:2px solid lightblue;text-align:center"| 23
 +
| style="border:2px solid lightblue;text-align:center"| 26
 +
|-
 +
| style="border:2px solid lightblue;text-align:center"| 12
 +
| style="border:2px solid lightblue;text-align:center"| 5520
 +
| style="border:2px solid lightblue;text-align:center"| 6120
 +
| style="border:2px solid lightblue;text-align:center"| 1.5
 +
| style="border:2px solid lightblue;text-align:center"| 0.7
 +
|-
 +
| style="border:2px solid lightblue;text-align:center" rowspan="2| Magdalena river
 +
| style="border:2px solid lightblue;text-align:center"| 12
 +
| style="border:2px solid lightblue;text-align:center"| 6000
 +
| style="border:2px solid lightblue;text-align:center"| 4000
 +
| style="border:2px solid lightblue;text-align:center"| 7
 +
| style="border:2px solid lightblue;text-align:center"| 7
 +
|-
 +
| style="border:2px solid lightblue;text-align:center"| 12
 +
| style="border:2px solid lightblue;text-align:center"| 6000
 +
| style="border:2px solid lightblue;text-align:center"| 8000
 +
| style="border:2px solid lightblue;text-align:center"| 0
 +
| style="border:2px solid lightblue;text-align:center"| 0.1
 +
|-
 +
| style="border:2px solid lightblue;text-align:center" rowspan="3| Neretva
 +
 +
| style="border:2px solid lightblue;text-align:center"| 8
 +
| style="border:2px solid lightblue;text-align:center"| 800
 +
| style="border:2px solid lightblue;text-align:center"| 300
 +
| style="border:2px solid lightblue;text-align:center"| 20
 +
| style="border:2px solid lightblue;text-align:center"| 15
 +
|-
 +
| style="border:2px solid lightblue;text-align:center"| 8
 +
| style="border:2px solid lightblue;text-align:center"| 800
 +
| style="border:2px solid lightblue;text-align:center"| 400
 +
| style="border:2px solid lightblue;text-align:center"| 10
 +
| style="border:2px solid lightblue;text-align:center"| 6.5
 +
|-
 +
| style="border:2px solid lightblue;text-align:center"| 8
 +
| style="border:2px solid lightblue;text-align:center"| 800
 +
| style="border:2px solid lightblue;text-align:center"| 500
 +
| style="border:2px solid lightblue;text-align:center"| 5
 +
| style="border:2px solid lightblue;text-align:center"| 2.9
 +
|}
  
−
==Comparison with observations==
 
  
−
The Rhône (France) and the Ebro (Spain) are examples of estuaries with almost no tidal motion (both situated on the Mediterranean coast). Figure 2 shows the observed dimensionless salt wedge lengths <math>C_i L / h</math> in these estuaries for different internal river Froude numbers <math>F_i</math>. The observed lengths are compared with the theoretical result for a prismatic estuary (Eq. (7)). For low-medium discharges the correspondence with theory is fairly good. For very small river flow the model lengths are much larger than the observed intrusion lengths. This is due in particular to the presence of high sills in the upstream part of the Rhône estuary (at 35 km from the mouth) and Ebro estuary (at 32 km from the mouth). Other less pronounced sills situated downstream also tend to arrest the salt wedge for a certain range of river discharges; the salt wedge length <math>L</math> therefore does not increase continuously as a function of <math>F_i</math>, as would be the case for a true prismatic canal.   
 
  
 
==Related articles==
 
==Related articles==
 +
:[[Estuarine circulation]]
 +
:[[Seawater density]]
 +
:[[Seawater intrusion and mixing in estuaries]]
  
−
[[Seawater intrusion and mixing in estuaries]]
 
−
 
−
[[Estuarine circulation]]
 
  
 
==References==
 
==References==
Line 81: Line 241:
 
|AuthorName=Dronkers J}}
 
|AuthorName=Dronkers J}}
  
 +
[[Category:Physical coastal and marine processes]]
 
[[Category:Estuaries and tidal rivers]]
 
[[Category:Estuaries and tidal rivers]]
 
[[Category:Hydrodynamics]]
 
[[Category:Hydrodynamics]]
−
[[Category:Land and ocean interactions]]
 

Latest revision as of 16:48, 7 December 2022

Definition of Salt wedge:
Seawater intrusion in an estuary as a wedge-shaped bottom layer which hardly mixes with the overlying fresh water layer. Salt wedges occur in estuaries where tidal motion is very weak or absent.
This is the common definition for Salt wedge, other definitions can be discussed in the article

Introduction

In estuaries where tidal motion is very weak or absent, seawater intrudes in the form of a wedge along the bottom, as a consequence of the higher density of seawater compared to fresh water. The intrusion length depends essentially on two parameters: river flow velocity [math]v[/math] and water depth [math]h[/math]. This article deals with the hydrodynamic balances that determine the salt wedge, illustrated by a model for a prismatic estuary (uniform depth and width). We follow the derivation first given by Schijf and Schönfeld in 1953 [1].

In most estuaries, seawater intrusion is strongly influenced by tidal motion (see Estuarine circulation). Even in microtidal estuaries this influence is often significant [2]. In some cases, especially in the Mediterranean Sea, tides are so small that their influence on seawater intrusion is minor. This article focuses on such situations; we assume that the salt wedge is not significally altered during the slight tidal motion up and down the estuary.

Seawater intrusion process

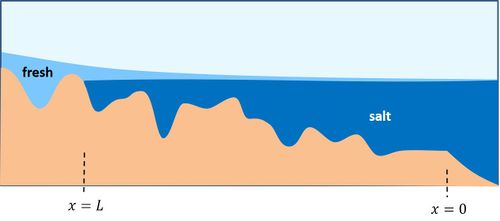
Figure 1: Longitudinal section of river with a fictitious corrugated sloping bottom. The sea boundary is at [math]x=0[/math]. The river discharge is very small; the upper boundary of the salt wedge is almost horizontal. The salt intrusion length [math]L[/math] corresponds to the location where the level of the river bed equals the sea level.

First consider the case of a very small river discharge such that the stress it exerts on the salt wedge is not significant. The absence of forces leads to an equilibrium situation where the salt wedge slope is zero. The level of the river bed rises inland; at some point inland, the level is equal to the sea level. Seawater can enter the river that far. The salt intrusion length is determined by the intersection of the sea level with the river bed, see Fig. 1.

In general, the shear stress exerted by the river on the intruding seawater cannot be neglected. We consider a situation without tide or a very small tide (tidal flow velocities much less than the flow velocity due to river discharge) and constant river discharge. We then have a stationary salt wedge, also called 'arrested salt wedge'. Except for extreme river discharges, the rate at which river water flows over the seawater wedge is not fast enough to produce complete mixing of the water column. However, the river flow velocity is high enough to produce a thin mixing layer. The river water exerts a shear stress on the seawater wedge via this mixing layer. The surface of the seawater wedge is therefore inclined (the pycnocline), such that the hydrostatic force (due to the slopes of the salt wedge and the water surface) balances the shear stress, see Fig. 2. The thin mixing layer is generally turbulent; the shear stress is therefore proportional to the square of the velocity difference over the mixing layer and it is assumed that it can be parameterized as the product of the river flow velocity squared and a shear stress coefficient [math] C_i [/math]. In theory, this coefficient should have a certain fixed value, but experimental observations yield various values.

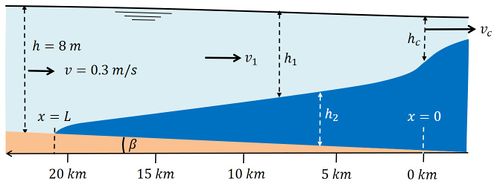
Figure 2: Longitudinal section of a salt wedge in a prismatic estuary. The sea boundary is situated at [math]x[/math]=0. The shape of the salt wedge shown in the figure corresponds to the theoretical curve (solution of Eq. (1)) for 8 m water depth, river flow velocity 0.3 m/s, salt layer density 1020 kg/m3 (internal river Froude number [math]F_i[/math]=0.24) and interfacial shear stress coefficient [math]C_i[/math]=0.00025.

The reason is that the ideal situation of a stationary salt wedge hardly occurs in practice. The river discharge varies, the tide is not negligibly small, extra turbulence is caused by a non-uniform river geometry, by waves, wind and shipping. Numerical models can partly quantify these influences, but it is difficult to accurately predict the salt intrusion length.


Seawater intrusion length

If the tide has a significant influence on the seawater intrusion process, an estuarine circulation is generated; this situation is discussed in the article Estuarine circulation. Here we assume the simpler case that the influence of the tide can be neglected. In the special case that the river geometry can be approached by a prismatic channel (uniform depth and width, no bottom slope). The relative depth of the upper fresh water layer [math]y=h_1/h[/math] then satisfies the differential equation (see Appendix)

[math] \large\frac{d}{dx} \normalsize [ -4 y^5 + 5y^4 - 10 F_i^2 y(2-y) ] = 20 \large \frac{C_i F_i^2}{h} \normalsize , \qquad (1) [/math]

where the internal Froude number [math]F_i[/math] is given by

[math]F_i = \large \frac{Q}{hb} \normalsize [ \epsilon g h]^{-1/2} , \qquad (2)[/math]

[math]Q[/math]= river discharge, [math]h[/math]= river depth, [math]b[/math]= river width and [math]\epsilon=\large \frac{\Delta \rho}{\rho} \normalsize [/math]= relative density difference of seawater and river water. The differential equation (1) is easily integrated if conditions at both boundaries of the salt wedge are known.

The conditions at the tip of the salt wedge is obvious: [math]y=1[/math] at [math]x=L [/math].

The condition at the sea boundary is more subtle. The upper layer depth cannot be zero because no fresh water could be discharged to the sea. When during the process of seawater intrusion the depth of the upper layer at the sea boundary decreases, the outflow velocity [math]v_1[/math] increases. However, the intrusion process stops when the outflow velocity equals the critical velocity [math]v_c[/math]. This is because a further upward shift of the interface boundary at sea cannot propagate upstream into the river. The critical velocity for upstream propagation of a perturbation at the interface is given by

[math]v_c=[\large \frac{\Delta \rho}{\rho} \normalsize g h_1]^{1/2} . \qquad (3) [/math]

Substitution in Eq. (2) gives [math]F_i = \large \frac{h_1 v_c}{h} \normalsize [\large \frac{\Delta \rho}{\rho} \normalsize g h]^{-1/2} = \large(\frac{h_1}{h})^{3/2}\normalsize = y(0)^{3/2}[/math],

from which it follows that the boundary conditions at the sea boundary [math]x=0[/math] is given by [math]y(0) = F_i^{2/3} . \qquad (4)[/math]

Integration of the differential equation with the two boundary conditions gives the length [math]L[/math] at constant river discharge:

[math]L = \Large \frac{h}{20 C_i} \normalsize (-10+15F_i^{2/3}-6F_i^{4/3}+F_i^{-2}) . \qquad (5)[/math]

In this expression, the salt intrusion length is inversely proportional to the interfacial shear stress coefficient [math]C_i[/math]. The value of this coefficient cannot be determined via the model and must therefore be determined independently.

The dimensionless salt wedge length [math]C_i L / h[/math] as a function of the internal river Froude number [math]F_i[/math] is shown in Fig. 3. The condition at the sea boundary plays a crucial role for the salt wedge length. The depth of the river outflow layer [math]h_1(0)[/math] is proportional to the river discharge at the power 2/3, according to the equations (2) and (4). Therefore the depth of the salt wedge layer at the mouth, [math]h_2(0)[/math], becomes very small for high river discharge.

Integration of Eq. (1) also gives the shape of the seawater wedge, shown in Fig. 2 for particular values of river depth, river discharge and shear stress coefficient [math] C_i [/math].

Generally, the analytical model cannot be used for predicting salt intrusion at low river discharge. This is an important limitation, because precisely this information is often most relevant in practice. The problem is that there is no analytical solution to the equations in the case of a sloping river bed. At low river runoff, the seawater intrudes thus far that the influence of the bottom slope cannot be neglected. In that case, the equations describing the seawater intrusion must be solved numerically. For rivers with a strongly sloping river bed, a first estimate of the salt intrusion length at low river discharge is obtained by the intersection of the seawater level with the river bottom, as shown in Fig. 1.

Additional mixing of river water and sea water can occur as a consequence of local river contractions, sharp river bends and high bottom sills. In these cases too, the analytical solution is less reliable and it is better to use a numerical model to determine the seawater intrusion.


Comparison with observations

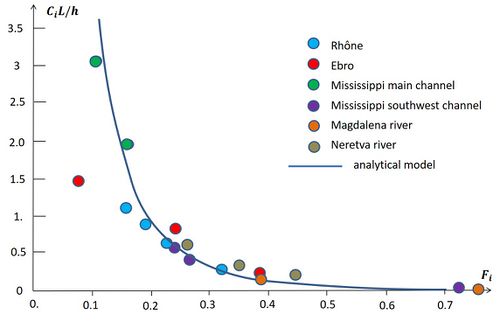
Figure 3: Dimensionless salt wedge length [math]C_i L / h[/math] according to Eq. (5) for a prismatic estuary and observed salt wedge lengths in the Rhône, Ebro [3], the Mississippi [4], Magdalena[5] and Neretva[6] estuaries at different discharges (corresponding to different internal river Froude numbers [math]F_i[/math]). For all estuaries the same value is used for the interfacial shear stress coefficient, [math]C_i[/math]=0.00025. Other parameters are indicated in Table 1.

The Rhône (France) and the Ebro (Spain) are examples of estuaries with almost no tidal motion (both situated on the Mediterranean coast, tidal amplitude in the order of 0.1 m on average). The tidal amplitude for the Mississippi at the US Gulf coast is in the order of 0.25 m on average; the tidal current velocities are small, but not much smaller than the river flow velocities for the lowest discharges considered in the comparison. The Magdalena (Colombia) discharges into the Caribbean Sea with a predominantly diurnal, mixed microtidal regime. The tidal range of 0.13 m to 0.40 m produces small tidal velocities that shift the salt water front over a distance of about 300 m[7].

Figure 3 shows the observed dimensionless salt wedge lengths [math]C_i L / h[/math] in these estuaries for different internal river Froude numbers [math]F_i[/math]. The observed lengths are compared with the theoretical result for a prismatic estuary (Eq. (5)), where the same interfacial shear stress coefficient is used for all the estuaries. For very small river flow the model lengths are much larger than the observed intrusion lengths. This is due in particular to the presence of high sills in the upstream part of the Rhône estuary (at 35 km from the mouth) and Ebro estuary (at 32 km from the mouth). Other less pronounced sills situated downstream also tend to arrest the salt wedge for a certain range of river discharges; the salt wedge length [math]L[/math] therefore does not increase continuously as a function of [math]F_i[/math], as would be the case for a true prismatic canal. The reasonable correspondence between observed and computed salt intrusion lengths for low-to-mean river discharges does not imply that the value of the interfacial shear stress coefficient, [math]C_i=0.00025[/math], should hold in general. In the present comparison this coefficient includes the effect of several factors by which the analytical model deviates from the real estuaries, such as deviations from the prismatic geometry (bed slope, sills, etc.) and tidal influence.


Appendix 1: Analytical model for a prismatic estuary

The following is a simple two-layer description of seawater intrusion in a microtidal prismatic (uniform width and depth) estuary. The salt wedge is represented by a separate layer of thickness [math]h_2[/math] along the bottom of the estuary, see figure 2. The total water depth [math]h[/math] is the sum of the bottom layer thickness [math]h_2[/math] and the upper surface layer thickness [math]h_1[/math]. Lateral variations of depth, density (salinity) and velocity are ignored. The velocity is indicated by [math]v[/math] and the density by [math]\rho[/math]. Subscripts 1 and 2 indicate the surface layer and the bottom layer respectively.

The pressure gradient [math]d p_2 / d x[/math] in the lower layer is related to the slope of the salt wedge (relative to a horizontal reference plane) and to the pressure gradient exerted by the overlying fresh water,

[math]\Large \frac{d p_2}{d x} \normalsize = g \rho_2 ( \beta + \Large \frac{d h_2}{d x} \normalsize )+ g \rho_1 \Large \frac{d h_1}{d x} \normalsize , \qquad (A1) [/math]

where [math]\rho_1=\rho[/math] is the fresh water density, [math]\rho_2=\rho+ \Delta \rho[/math] the seawater density and [math]\beta[/math] the bottom slope. Other symbols are shown in Fig. 2. Because of the lower density of fresh water compared to seawater, this pressure gradient generally acts in upstream direction. A counteracting pressure gradient is produced by friction at the interface (pycnocline) induced by the overlying river flow. The shear stress [math]\tau_i[/math] exerted by river flow on the salt wedge is parameterized as [math]\tau_i / \rho = C_i v_1^2 [/math], where [math]C_i[/math] is the interfacial shear stress coefficient of order [math]10^{-4}-10^{-3} .[/math][8]

The salt wedge intrusion is also influenced by bottom friction. However, in a stationary situation bottom friction does not play a role because the salt wedge is at rest.

River flow is confined to the upper layer which becomes thinner in downstream direction. The resulting spatial acceleration of river flow creates a gradient in the hydraulic head given by [math]\rho v_1 d v_1 / d x .[/math] The surface layer is further subjected to a pressure gradient related to the water surface slope (relative to a horizontal reference plane),

[math]\Large \frac{d p_1}{d x} \normalsize = g \rho_1 ( \beta + \Large \frac{d h_2}{d x} + \frac{d h_1}{d x} \normalsize) , \qquad (A2) [/math]

and to the interfacial shear stress [math]\tau_i .[/math] The stationary hydrodynamic balance of the two layers is therefore given by the equations

[math]\Large \frac{d p_2}{\rho_2 d x} + \frac{\tau_i}{\rho h_2} \normalsize = 0; \; \Large \frac{d p_1}{\rho_1 d x} \normalsize + v_1 \; \Large \frac{d v_1}{d x} - \frac{\tau_i}{\rho h_1} \normalsize = 0 . \qquad (A3)[/math]

In a prismatic estuary the depth [math]h[/math] and width [math]b[/math] do not vary along the channel axis. By subtracting the two layer equations the salt wedge slope [math]d h_2 / d x[/math] and the bottom slope [math]\beta[/math] are eliminated. By assuming that the bottom slope is not much larger than the surface slope (water depth [math]h[/math] approximately constant), we can substitute [math]h_2 \approx h-h_1[/math]. The velocity in the upper layer [math]v_1[/math] can be eliminated from the equations by using the condition of continuity of river discharge per unit width,

[math]h_1 v_1 = h v = Q / b, \qquad (A4) [/math]

where [math]Q[/math] is the river discharge. These manipulations lead to the ordinary nonlinear differential equation for the variable [math]y=h_1 / h[/math],

[math] (y^3-F_i^2)(1-y) \large\frac{dy}{dx} \normalsize = \large \frac{C_i F_i^2}{h} \normalsize , \qquad (A5) [/math]

with [math]F_i = \large \frac{Q}{hb} [ \frac{gh \Delta \rho}{ \rho}]^{-1/2} \normalsize .[/math]

This is equivalent to Eq. (1) indicated above.


Appendix 2: Parameters of a few salt wedge estuaries

Table 1. Data of observed salt wedge lengths for the Rhône (France)[3] and Ebro (Spain)[3], the Mississippi (US)[4], Magdalena (Colombia)[5] and Neretva (Croatia)[6] estuaries. The indicated depths are not mean depths, but the smallest depths along the thalweg below the salt wedge taking into account natural sills.
Estuary depth [m] cross section [m2] river discharge [m3/s] observed salt wedge intrusion length [math]L[/math] [km] [math]L[/math] from Eq. (5), [math]C_i=2.5 \, 10^{-4}[/math]
Rhône 8 2500 500 35 53
8 2500 600 28 34
8 3000 850 20 23
8 3000 1200 9 9
Ebro 5.5 1000 80 32 177
5.5 1000 250 18 13
5.5 1000 400 5 3
Mississippi main channel 18 14220 2830 220 296
18 14220 4250 140 120
Mississppi southwest pass 14 6440 2550 32 35
14 6440 2830 23 26
12 5520 6120 1.5 0.7
Magdalena river 12 6000 4000 7 7
12 6000 8000 0 0.1
Neretva 8 800 300 20 15
8 800 400 10 6.5
8 800 500 5 2.9


Related articles

Estuarine circulation
Seawater density
Seawater intrusion and mixing in estuaries


References

  1. ↑ Schijf, J.B., Schönfeld, J.C. 1953. Theoretical considerations on the motion of salt and fresh water. Proceedings of the 5th I.A.H.R. Congress, 321–333
  2. ↑ Geyer, R.W. and Farmer, D.H. 1989. Tide-induced variation of the dynamics of a salt wedge estuary. J. Phys. Oceanography 19: 1060-1072
  3. ↑ 3.0 3.1 3.2 Ibanez, C., Pont, D. and Prat, N. 1997. Characterization of the Ebre and Rhone estuaries: A basis for defining and classifying salt-wedge estuaries. Limnol. Oceanogr. 42: 89–101
  4. ↑ 4.0 4.1 Rattray, M. Jr and Mitsuda, E. 1974. Theoretical analysis and conditions in a salt wedge. Estuarine and Coastal Marine Science 2: 375-394
  5. ↑ 5.0 5.1 Arevalo, F.M., Alvarez-Silva, O., Caceres-Euse, A. and Cardona, Y. 2022. Mixing mechanisms at the strongly-stratified Magdalena River’s estuary and plume. Estuarine, Coastal and Shelf Science 277, 108077
  6. ↑ 6.0 6.1 Krvavica, N., Gotovac, H. and Loncar, G. 2021. Salt-wedge dynamics in microtidal Neretva River estuary. Regional Studies in Marine Science 43, 101713
  7. ↑ Ospino, S., Restrepo, J.C., Otero, L., Pierini, J. and Alvarez-Silva, O. 2018. Saltwater intrusion into a river with high fluvial discharge: a microtidal estuary of the Magdalena River, Colombia. J. Coast Res. 34: 1273–1288
  8. ↑ Abraham, G., Karelse, M. and Van Os, A.G. 1979. On the magnitude of the interfacial shear stress of subcritical stratified flows in relation with interfacial stability. Hydr. Res. 17: 273-287
The main author of this article is Job Dronkers
Please note that others may also have edited the contents of this article.
Citation: Job Dronkers (2022): Salt wedge estuaries. Available from http://www.coastalwiki.org/wiki/Salt_wedge_estuaries [accessed on 25-11-2024]
Retrieved from "https://www.coastalwiki.org/w/index.php?title=Salt_wedge_estuaries&oldid=79953"