Difference between revisions of "Wave-induced soil liquefaction"
Dronkers J (talk | contribs) |
Dronkers J (talk | contribs) |
||
| Line 1: | Line 1: | ||
| + | |||
{{ Definition| title = Soil liquefaction | {{ Definition| title = Soil liquefaction | ||
| Line 4: | Line 5: | ||
| − | Submerged soils which are not well consolidated are prone to liquefaction when subjected to strong shaking. Soil liquefaction can be produced by earthquakes, but here we concentrate on submarine soils which are subjected to cyclic loading by waves. Structures built on freshly deposited submarine soils can collapse or sink when the seabed is liquified. | + | Submerged soils which are not well consolidated are prone to liquefaction when subjected to strong shaking. Soil liquefaction can be produced by earthquakes, but here we concentrate on submarine soils which are subjected to cyclic loading by waves. Structures built on freshly deposited submarine soils can collapse or sink when the seabed is liquified. Mathematical derivations are given in the Appenix. |
| Line 14: | Line 15: | ||
[[File:TransientLiquefaction.jpg|thumb|right|350px|Fig. 1. Principle of transient soil liquefaction. After De Groot et al. 2006<ref name=G6>de Groot, M. B., Bolton, M. D., Foray P., Meijers, P., Palmer, A. C., Sandven, R., Sawicki, A. and The, T. C. 2006 Physics of Liquefaction Phenomena around Marine Structures. Journal of Waterway, Port, Coastal, and Ocean Engineering 132: 227-243</ref>]] | [[File:TransientLiquefaction.jpg|thumb|right|350px|Fig. 1. Principle of transient soil liquefaction. After De Groot et al. 2006<ref name=G6>de Groot, M. B., Bolton, M. D., Foray P., Meijers, P., Palmer, A. C., Sandven, R., Sawicki, A. and The, T. C. 2006 Physics of Liquefaction Phenomena around Marine Structures. Journal of Waterway, Port, Coastal, and Ocean Engineering 132: 227-243</ref>]] | ||
| − | The upper part of the seabed can be liquefied if the soil pore pressure near the bed surface is higher than the pressure exerted by the overlying water mass. This occurs when the pore pressure in the seabed follows (with some delay, depending on the soil permeability) the oscillating water pressure exerted by surface waves. The soil top layer then experiences an upward force during the passage of the wave trough, which lifts sediment particles near the seabed surface out of the soil skeleton, see Fig. 1. The soil top layer (typically ten | + | The upper part of the seabed can be liquefied if the soil pore pressure near the bed surface is higher than the pressure exerted by the overlying water mass. This occurs when the pore pressure in the seabed follows (with some delay, depending on the soil permeability) the oscillating water pressure exerted by surface waves. The soil top layer then experiences an upward force during the passage of the wave trough, which lifts sediment particles near the seabed surface out of the soil skeleton, see Fig. 1. The soil top layer (typically ten or a few tens of centimeters) becomes liquefied over a short period of time during which this condition prevails. One consequence is that objects deposited on the seabed can sink and become buried<ref>Klammler, H., Penko, A.M., Staples, T., Sheremet, A. and Calantoni, J. 2021. Observations and modeling of wave-induced burial and sediment entrainment: Likely importance of degree of liquefaction. Journal of Geophysical Research: Oceans 126, e2021JC017378</ref> or float up if the density of the object is less than that of the liquified soil. The combined effect of vertical and horizontal wave-induced pore pressure gradients promotes the development of a [[sheet flow]] layer<ref>Anderson, D., Cox, D., Mieras, R., Puleo, J.A. and Hsu, T.-J. 2017. Observations of wave-induced pore pressure gradients and bed level response on a surf zone sandbar. J. Geophys. Res. Oceans 122: 5169– 5193</ref>. Most observations of wave-induced transient liquefaction come from laboratory experiments. There are also studies based on field observations, in the nearshore subtidal zone and in the intertidal zone. In the latter case it was found that a small volume fraction of air in the soil can greatly dampen the transmission of wave-induced water pressure to the pore fluid<ref name=M9>Michallet, H., Mory, M. and Piedra-Cueva, I. 2009. Wave-induced pore pressure measurements near a coastal structure, J. Geophys. Res. 114, C06019</ref>. |
<br clear=all> | <br clear=all> | ||
| Line 34: | Line 35: | ||
Flume experiments show that the liquefaction potential strongly depends on the soil composition. Experiments by Gratchev et al. (2006<ref>Gratchev, I.B., Sassa, K., Osipov, V.I. and Sokolov, V.N. 2006. The liquefaction of clayey soils under cyclic loading. Eng. Geol. 86: 70–84</ref>) revealed the significant influence of plasticity on soil liquefaction resistance. Soil vulnerable to liquefaction had an open microfabric in which clay aggregates mainly gathered at the silt particle contact points, forming low-strength 'clay bridges' that were easily destroyed during cyclic loading (Fig. 2). The contact friction between particles that maintained the soil skeleton structure was reduced by the clay aggregates, so grains could easily slip and rotate once the seabed was subjected to wave loading. Clay content thus enhances the plasticity and compressibility of the clay-silt seabed and increases the sensitivity of the seabed to liquefaction. | Flume experiments show that the liquefaction potential strongly depends on the soil composition. Experiments by Gratchev et al. (2006<ref>Gratchev, I.B., Sassa, K., Osipov, V.I. and Sokolov, V.N. 2006. The liquefaction of clayey soils under cyclic loading. Eng. Geol. 86: 70–84</ref>) revealed the significant influence of plasticity on soil liquefaction resistance. Soil vulnerable to liquefaction had an open microfabric in which clay aggregates mainly gathered at the silt particle contact points, forming low-strength 'clay bridges' that were easily destroyed during cyclic loading (Fig. 2). The contact friction between particles that maintained the soil skeleton structure was reduced by the clay aggregates, so grains could easily slip and rotate once the seabed was subjected to wave loading. Clay content thus enhances the plasticity and compressibility of the clay-silt seabed and increases the sensitivity of the seabed to liquefaction. | ||
| − | Experiments with kaolinite-fine sand and illite-fine sand showed that the susceptibility of a soil to liquefaction increases with increasing clay content if the clay content is low (0.5-5%), but decreases with a higher clay content<ref>Zang, J., Jiang, Q., Jeng, D., Zhang, C., Chen, X. and Wang, L. 2020. Experimental Study on Mechanism of Wave-Induced Liquefaction of Sand-Clay Seabed. J. Mar. Sci. Eng. 8, 66</ref>. At a clay content of more than 10-30%, depending on the type of clay, the silt-clay mixture was not susceptible to liquefaction. This can be explained by the fact that in case of high clay content the silt grains are completely encapsulated in the clay matrix and therefore cannot rearrange under cyclic shear stresses, | + | Experiments with kaolinite-fine sand and illite-fine sand showed that the susceptibility of a soil to liquefaction increases with increasing clay content if the clay content is low (0.5-5%), but decreases with a higher clay content<ref>Zang, J., Jiang, Q., Jeng, D., Zhang, C., Chen, X. and Wang, L. 2020. Experimental Study on Mechanism of Wave-Induced Liquefaction of Sand-Clay Seabed. J. Mar. Sci. Eng. 8, 66</ref>. At a clay content of more than 10-30%, depending on the type of clay, the silt-clay mixture was not susceptible to liquefaction. This can be explained by the fact that in case of high clay content the silt grains are completely encapsulated in the clay matrix and therefore cannot rearrange under cyclic shear stresses, causing resistance to liquefaction. Experiments by Kirca et al. (2014<ref>Kirca, V., Sumer, B.M. and Fredsøe, J. 2014. Influence of clay content on wave-induced liquefaction, J. Waterw. Port Coast. Ocean Eng. ASCE 140, 04014024</ref>) showed that the sensitivity of a sand-clay mixture to wave-induced liquefaction not only depends on the clay content but also on the sand grainsize. Liquefaction occurred at a much larger clay content for medium sand than for fine sand or silt. The presence of shell fragments also decreases the susceptibility of silt to liquefaction<ref name=S20/>. Experiments for a medium-sand-clay (kaolinite) seabed supporting a submerged breakwater showed that wave-induced liquefaction required a clay content greater than 40%<ref>Chavez, V., Mendoza, E., Silva, R., Silva, A. and Losada, M.A. 2017. An experimental method to verify the failure of coastal structures by wave induced liquefaction of clayey soils. Coastal Engineering 123: 1–10</ref>. These experiment also showed that the initial water content in the soil is relevant to the liquefaction potential as it affects the pressure build-up process. Higher pore water fractions allow the residual pore pressure to accumulate faster. |
| Line 47: | Line 48: | ||
| + | ==Related articles== | ||
| + | :[[ Stability of rubble mound breakwaters and shore revetments]] | ||
| − | == | + | ==Appendix== |
| − | :[[ | + | |
| + | ===Transient liquefaction=== | ||
| + | According to linear wave theory (see [[Shallow-water wave theory]]) the pressure exerted on the seabed by a propagating sinusoidal wave is given by | ||
| + | |||
| + | <math>p_{seafloor} (x,t) = p_0 \cos \Big( 2 \pi (\large\frac{x}{L}-\frac{t}{T}\normalsize)\Big) , \quad p_0 = \Large\frac{ \rho g a}{\cosh(2 \pi h/L)} \normalsize, \qquad (1) </math> | ||
| + | |||
| + | where <math>x=</math> coordinate wave propagation direction, <math>t=</math> time, <math>g=</math> gravitational acceleration, <math>\rho=</math> seawater density, <math>a=</math> wave amplitude, <math>L=</math> wavelength, <math>T=</math> wave period, <math>h=</math> water depth. | ||
| + | |||
| + | We consider loose-packed homogeneous soil consisting of fine sand, with fractions of silt and clay. The soil characteristics are: | ||
| + | *<math>n</math> porosity of the soil, i.e. the volume left for pore water and gaz (air) | ||
| + | *<math>k</math> [m/s] soil permeability (= hydraulic conductivity) | ||
| + | *<math>G</math> [Pa] [https://en.wikipedia.org/wiki/Shear_modulus shear modulus] of soil (= modulus of rigidity = the ratio of shear stress and shear strain) | ||
| + | *<math>\nu</math> [https://en.wikipedia.org/wiki/Poisson%27s_ratio Poisson ratio] of soil (= amount of transversal elongation divided by the amount of vertical compression) | ||
| + | *<math>\beta</math> [Pa] [https://en.wikipedia.org/wiki/Bulk_modulus bulk modulus] (the ratio of pressure increase and relative volume decrease = inverse of compressibility) of pore water and included air | ||
| + | Typical values for loosely packed soil of fine sand with a small fraction of silt an clay, saturated and including a small fraction (order 1‰) of included air: | ||
| + | <math>n=0.4, \; k=10^{-5} m/s, \; G=10^7 Pa, \; \beta=10^8 Pa, \; \nu=0.49</math>. | ||
| + | For illustration we consider waves with period <math>T =</math> 10 s and wavelength <math>L=</math> 70 m. | ||
| + | |||
| + | The wave load applies over a large stretch of order <math>L/(2 \pi)</math> length, which excludes substantial lateral soil dilation. We thus focus on the vertical compression <math>dV/dt</math> of a small soil volume element <math>V</math> resulting from the wave-induced varying pressure load at the soil surface Eq. (1). The compression <math>dV/dt</math> is due to: | ||
| + | # the compression of the pore fluid, <math>\Large\frac{dV_1}{dt}\normalsize = V \Large\frac{n}{\beta}\frac{\partial p}{\partial t}\normalsize ,</math> where <math>p(z,t)</math> is the pore fluid pressure at depth <math>z</math> below the seafloor, <math>n</math> is the porosity (i.e. the volume left for pore water and enclosed air) and <math>\beta</math> is the bulk modulus of the pore water and gaz. | ||
| + | # the pore water outflow, <math>\Large\frac{dV_2}{dt}\normalsize = V \Large\frac{\partial u}{\partial z}\normalsize = V \Large\frac{k}{\rho g}\frac{\partial^2 p}{\partial z^2}\normalsize , </math> where <math>u</math> is the pore water vertical flow velocity, and <math>k</math> is the soil permeability. The last equation follows from Darcy's law. | ||
| + | The volume compression creates a change in the volumetric strain (also called 'bulk strain') <math>d\epsilon=\Large\frac{1}{V}\normalsize (dV_1+dV_2)</math>, | ||
| + | |||
| + | <math>\Large\frac{d \epsilon}{dt}\normalsize = \Large\frac{n}{\beta}\frac{\partial p}{\partial t}\normalsize + \Large\frac{k}{\rho g}\frac{\partial^2 p}{\partial^2 z}\normalsize . \qquad (2)</math> | ||
| + | |||
| + | The volumetric strain is related by Hooke's law to the effective stress (inter-grain stress) by the formula <math>\epsilon = -m_v (\sigma - p) ,</math> where <math>\sigma</math> is the total stress applied to the soil volume <math>V</math> and <math>p</math> the pore pressure. The compressibility modus <math>m_v</math> can be expressed as a function of the soil shear modulus <math>G</math> and the Poisson ratio <math>\nu</math>, <math>\; m_v = \Large\frac{1-2 \nu}{2 G (1-\nu)}\normalsize .</math> | ||
| + | |||
| + | Eq. (2) can be rewritten after some manipulation as a differential equation from which the pore pressure <math>p(z,t)</math> can be solved: | ||
| + | |||
| + | <math>\Large\frac{\partial p}{\partial t}\normalsize = c_s \Large\frac{\partial \sigma}{\partial t}\normalsize + c_v \Large\frac{\partial^2 p}{\partial z^2}\normalsize , \quad c_s = \Large\frac{1}{1+m}\normalsize , \quad c_v = \Large\frac{k \beta}{\rho g n}\frac{m}{1+m}\normalsize , \qquad m = 2 n \Large\frac{G}{\beta}\frac{1-\nu}{1-2 \nu}\normalsize . \qquad (3)</math> | ||
| + | |||
| + | The total stress <math>\sigma</math> is the pressure transmitted by the surface wave to the pore fluid and can be approximated by <math>\sigma \approx p_0 \exp(-2 \pi z / L) \cos(2 \pi t /T)</math>, where <math>z</math> is the depth below the seafloor. | ||
| + | The solution of Eq. (3) for a homogeneous soil layer of very large (infinite) depth is (assuming <math>L^2 >> 2 \pi c_v T</math>) | ||
| + | |||
| + | <math>p(x,z,t) \approx p_0 \Bigg[ \large\frac{1}{1+m}\normalsize e^{- 2\pi \large \frac{z}{L}\normalsize} \cos \Big( 2 \pi (\large\frac{x}{L}-\frac{t}{T}\normalsize)\Big) + \large\frac{m}{1+m}\normalsize e^{-\Large\frac{z}{d}\normalsize} \cos \Big( 2 \pi (\large\frac{x}{L}-\frac{t}{T}+\frac{z}{d}\normalsize)\Big) \Bigg] .\qquad (4)</math> | ||
| + | |||
| + | The depth <math>d</math> is given by | ||
| + | |||
| + | <math>d = \Big( \Large\frac{T \, k \, \beta \, m}{\pi \, \rho \, n \, g \, (1+m)}\normalsize \Big)^{1/2} . \qquad (5)</math> | ||
| + | |||
| + | Substitution of the values of the numerical illustration gives <math>d \approx</math> 70 cm. Over the top 10 cm the second term in the r.h.s. of Eq. (4) dominates with respect to the first term. Over this depth, wave-induced pressure fluctuations are substantial and is the soil susceptible to transient liquefaction. | ||
| + | |||
| + | For more densely packed soil, the values of the shear modulus are larger and the values of the Poisson ratio are smaller. In this case the first term in the r.h.s. of Eq. (4) dominates. The wave-induced pressure fluctuations penetrate to greater depth into the soil, but the soil is less susceptible to liquefaction. | ||
| + | |||
| + | For liquefaction, the pressure gradient near the soil surface must be larger than the submerged weight of the soil grains. The pressure gradient at <math>z=0</math> depends mainly on the second term in the r.h.s. of Eq. (4) for the soil characteristics considered. This condition reads | ||
| + | |||
| + | <math>\Large\frac{m}{1+m}\frac{p_0}{d}\normalsize > g (\rho_{soil} - \rho) . \qquad (4)</math> | ||
| + | |||
| + | In the numerical example, liquefaction occurs if the wave height exceeds 4.5 m. | ||
| + | |||
| + | |||
| + | ===Residual liquefaction=== | ||
| + | For transient liquefaction it has been assumed that the volumetric soil strain <math>\epsilon</math> under wave loading is cyclic. According to the soil mechanics theory of Therzagi (1925<ref>Terzaghi, K. 1925. Principles of Soil Mechanics: IV—Settlement and consolidation of clay. Engineering News-Record 95(22): 874-878</ref>), the strain <math>\epsilon</math> gradually increases. We assume for simplicity that the total stress <math>\sigma</math> increases throughout the soil in proportion to the number <math>N</math> of wave cycles, | ||
| + | |||
| + | <math>\sigma \propto N \, p_0 \quad</math> or <math>\quad \Large\frac{d \sigma}{dt}\normalsize \propto \Large\frac{p_0}{T}\normalsize</math>. | ||
| + | |||
| + | Instead of Eq. (3) we now have the following equation for the wave-averaged pore pressure <math>\overline{p}(z,t)</math> : | ||
| + | |||
| + | <math>\Large\frac{\partial \overline{p}}{\partial t}\normalsize= B \Large\frac{p_0}{T} + c_v \Large\frac{\partial^2 \overline{p}}{\partial x^2}\normalsize , \qquad (5)</math> | ||
| + | |||
| + | where <math>B</math> is a proportionality constant dependent on the soil characteristics, that must be determined experimentally. An approximate solution of Eq. (5) can be found by assuming a parabolic depth dependence of the pore pressure for a homogeneous soil layer of thickness <math>D</math> <ref name=V6>Verruijt, A. 2006. Offshore soil mechanics. Delft University Lecture Notes</ref>. The boundary conditions are: for <math>z=0: \; \overline{p}(z,t)=0 \;</math> and for <math> \; z=D: \; \Large\frac{\partial \overline{p}}{\partial z}\normalsize =0 \;</math>. The solution is | ||
| + | |||
| + | <math>\overline{p}(z,t) = z(2D-z)\Large\frac{B p_0}{2 c_v T}\normalsize \Big[ 1 - e^{-\Large\frac{3 c_v t}{D^2}}\normalsize \Big] . \qquad (6)</math> | ||
| + | |||
| + | The dimensionless coefficient <math>B</math> represents the rate of pore pressure increase per unit applied maximum pressure load in one wave cycle due to soil compaction. For loosely packed soil this rate is of the order <math>B \approx 10^{-3}</math>; for densely packed soil <math>B</math> is much smaller<ref name=V6/>. The coefficient <math>B</math> has been assumed constant in Eq. (5), but in reality it will gradually decrease during soil compaction. The formula (6) therefore overestimates the real value of the pore pressure. | ||
| + | |||
Revision as of 11:08, 9 September 2023
Definition of Soil liquefaction:
When a water-saturated soil starts behaving as a fluid, losing stiffness and bearing capacity.
This is the common definition for Soil liquefaction, other definitions can be discussed in the article
|
Submerged soils which are not well consolidated are prone to liquefaction when subjected to strong shaking. Soil liquefaction can be produced by earthquakes, but here we concentrate on submarine soils which are subjected to cyclic loading by waves. Structures built on freshly deposited submarine soils can collapse or sink when the seabed is liquified. Mathematical derivations are given in the Appenix.
Contents
Two types of soil liquefaction
Two types of wave-induced soil liquefaction can be distinguished: Transient liquefaction (also called instantaneous or momentary liquefaction) and residual liquefaction. Both types can occur in poorly drained loosely packed soils, for example soils containing a high percentage of fine silty material. In well-drained soils, for example a medium-sand seabed, pore pressure by cyclic loading cannot build up, but transient liquefaction is possible.
Transient liquefaction
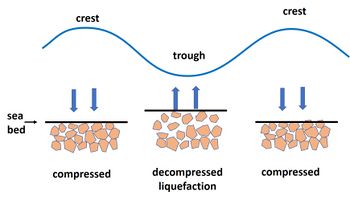
The upper part of the seabed can be liquefied if the soil pore pressure near the bed surface is higher than the pressure exerted by the overlying water mass. This occurs when the pore pressure in the seabed follows (with some delay, depending on the soil permeability) the oscillating water pressure exerted by surface waves. The soil top layer then experiences an upward force during the passage of the wave trough, which lifts sediment particles near the seabed surface out of the soil skeleton, see Fig. 1. The soil top layer (typically ten or a few tens of centimeters) becomes liquefied over a short period of time during which this condition prevails. One consequence is that objects deposited on the seabed can sink and become buried[2] or float up if the density of the object is less than that of the liquified soil. The combined effect of vertical and horizontal wave-induced pore pressure gradients promotes the development of a sheet flow layer[3]. Most observations of wave-induced transient liquefaction come from laboratory experiments. There are also studies based on field observations, in the nearshore subtidal zone and in the intertidal zone. In the latter case it was found that a small volume fraction of air in the soil can greatly dampen the transmission of wave-induced water pressure to the pore fluid[4].
Residual liquefaction
Here we consider a loosely packed water-saturated soil with slightly compressible pore water due to the presence of a small air fraction. The soil consists of fine sediments – fine sand, silt and clay – with poor drainage capacity (low hydraulic conductivity). When such a soil is subjected to cyclic wave-induced loading and associated shear deformations, the soil grains tend to rearrange such that the soil skeleton is progressively compressed. (The reverse happens for a densely compacted soil.) The resulting reduction of the pore volume is associated with an increase of the pore water pressure. When the pore pressure exceeds the pressure exerted by the load of the overlying water and soil (pore pressure higher than the initial mean normal effective stress, taking soil cohesion into account), the contact friction points between soil grains are broken and the soil skeleton collapses. The soil grains become unbound and completely free, carried by the pore water (Fig. 2). The soil begins to act like a liquid, losing its stiffness and bearing capacity. Any structure built on this soil will sink or collapse[5].
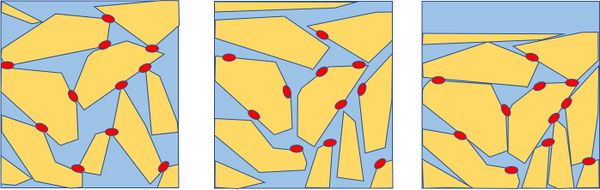
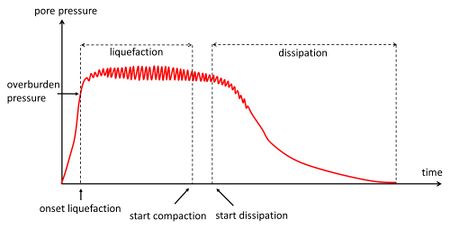
The onset of liquefaction occurs first at the surface of the bed, and rapidly spreads out across the soil depth, causing the entire soil to behave like a liquid. When the liquefaction reaches the impermeable base, the soil begins to compact. The pores between particles become gradually larger, allowing pore water drainage and wave-induced compaction. Soil grains fall out of the liquid state, settle through the pore water until they come into contact with each other. The compaction gradually progresses from the impermeable base in the upward direction, and the entire sequence of the liquefaction/compaction process comes to an end when the compaction reaches the soil surface[6][7]. After compaction, the soil will be much less susceptible to renewed liquefaction. The liquefaction-compaction process is depicted schematically in Fig. 3.
Influence of soil composition
Flume experiments show that the liquefaction potential strongly depends on the soil composition. Experiments by Gratchev et al. (2006[8]) revealed the significant influence of plasticity on soil liquefaction resistance. Soil vulnerable to liquefaction had an open microfabric in which clay aggregates mainly gathered at the silt particle contact points, forming low-strength 'clay bridges' that were easily destroyed during cyclic loading (Fig. 2). The contact friction between particles that maintained the soil skeleton structure was reduced by the clay aggregates, so grains could easily slip and rotate once the seabed was subjected to wave loading. Clay content thus enhances the plasticity and compressibility of the clay-silt seabed and increases the sensitivity of the seabed to liquefaction.
Experiments with kaolinite-fine sand and illite-fine sand showed that the susceptibility of a soil to liquefaction increases with increasing clay content if the clay content is low (0.5-5%), but decreases with a higher clay content[9]. At a clay content of more than 10-30%, depending on the type of clay, the silt-clay mixture was not susceptible to liquefaction. This can be explained by the fact that in case of high clay content the silt grains are completely encapsulated in the clay matrix and therefore cannot rearrange under cyclic shear stresses, causing resistance to liquefaction. Experiments by Kirca et al. (2014[10]) showed that the sensitivity of a sand-clay mixture to wave-induced liquefaction not only depends on the clay content but also on the sand grainsize. Liquefaction occurred at a much larger clay content for medium sand than for fine sand or silt. The presence of shell fragments also decreases the susceptibility of silt to liquefaction[7]. Experiments for a medium-sand-clay (kaolinite) seabed supporting a submerged breakwater showed that wave-induced liquefaction required a clay content greater than 40%[11]. These experiment also showed that the initial water content in the soil is relevant to the liquefaction potential as it affects the pressure build-up process. Higher pore water fractions allow the residual pore pressure to accumulate faster.
The soil in an actual field situation usually has a long history of wave action, and hence it normally is a consolidated stiff soil, with low sensitivity to wave-induced liquefaction. This does not hold for freshly deposited soils. This may be the case, for example, where a pipeline is laid in a trench, and the trench is then backfilled[5].
Fluid mud can be considered liquified soil. However, cohesive soil is not liquefied by the process of pore pressure build-up. Fluid mud is formed when a high suspended concentration of fine cohesive particles settles on the sea floor and forms a dense colloidal suspension. See Fluid mud.
Preventing soil liquefaction
The susceptibility of a soil to liquefaction can be checked through Standard Penetration Tests or Cone Penetration Tests. Liquefaction risks can be reduced by measures such as replacing soft soil (expensive) or by consolidation measures. Soil consolidation can be done for example by vibro compaction or by preloading the soft bed with coarse sediment[12]. Monitoring of the consolidation process should ensure that a stable situation is reached.
Related articles
Appendix
Transient liquefaction
According to linear wave theory (see Shallow-water wave theory) the pressure exerted on the seabed by a propagating sinusoidal wave is given by
[math]p_{seafloor} (x,t) = p_0 \cos \Big( 2 \pi (\large\frac{x}{L}-\frac{t}{T}\normalsize)\Big) , \quad p_0 = \Large\frac{ \rho g a}{\cosh(2 \pi h/L)} \normalsize, \qquad (1) [/math]
where [math]x=[/math] coordinate wave propagation direction, [math]t=[/math] time, [math]g=[/math] gravitational acceleration, [math]\rho=[/math] seawater density, [math]a=[/math] wave amplitude, [math]L=[/math] wavelength, [math]T=[/math] wave period, [math]h=[/math] water depth.
We consider loose-packed homogeneous soil consisting of fine sand, with fractions of silt and clay. The soil characteristics are:
- [math]n[/math] porosity of the soil, i.e. the volume left for pore water and gaz (air)
- [math]k[/math] [m/s] soil permeability (= hydraulic conductivity)
- [math]G[/math] [Pa] shear modulus of soil (= modulus of rigidity = the ratio of shear stress and shear strain)
- [math]\nu[/math] Poisson ratio of soil (= amount of transversal elongation divided by the amount of vertical compression)
- [math]\beta[/math] [Pa] bulk modulus (the ratio of pressure increase and relative volume decrease = inverse of compressibility) of pore water and included air
Typical values for loosely packed soil of fine sand with a small fraction of silt an clay, saturated and including a small fraction (order 1‰) of included air: [math]n=0.4, \; k=10^{-5} m/s, \; G=10^7 Pa, \; \beta=10^8 Pa, \; \nu=0.49[/math]. For illustration we consider waves with period [math]T =[/math] 10 s and wavelength [math]L=[/math] 70 m.
The wave load applies over a large stretch of order [math]L/(2 \pi)[/math] length, which excludes substantial lateral soil dilation. We thus focus on the vertical compression [math]dV/dt[/math] of a small soil volume element [math]V[/math] resulting from the wave-induced varying pressure load at the soil surface Eq. (1). The compression [math]dV/dt[/math] is due to:
- the compression of the pore fluid, [math]\Large\frac{dV_1}{dt}\normalsize = V \Large\frac{n}{\beta}\frac{\partial p}{\partial t}\normalsize ,[/math] where [math]p(z,t)[/math] is the pore fluid pressure at depth [math]z[/math] below the seafloor, [math]n[/math] is the porosity (i.e. the volume left for pore water and enclosed air) and [math]\beta[/math] is the bulk modulus of the pore water and gaz.
- the pore water outflow, [math]\Large\frac{dV_2}{dt}\normalsize = V \Large\frac{\partial u}{\partial z}\normalsize = V \Large\frac{k}{\rho g}\frac{\partial^2 p}{\partial z^2}\normalsize , [/math] where [math]u[/math] is the pore water vertical flow velocity, and [math]k[/math] is the soil permeability. The last equation follows from Darcy's law.
The volume compression creates a change in the volumetric strain (also called 'bulk strain') [math]d\epsilon=\Large\frac{1}{V}\normalsize (dV_1+dV_2)[/math],
[math]\Large\frac{d \epsilon}{dt}\normalsize = \Large\frac{n}{\beta}\frac{\partial p}{\partial t}\normalsize + \Large\frac{k}{\rho g}\frac{\partial^2 p}{\partial^2 z}\normalsize . \qquad (2)[/math]
The volumetric strain is related by Hooke's law to the effective stress (inter-grain stress) by the formula [math]\epsilon = -m_v (\sigma - p) ,[/math] where [math]\sigma[/math] is the total stress applied to the soil volume [math]V[/math] and [math]p[/math] the pore pressure. The compressibility modus [math]m_v[/math] can be expressed as a function of the soil shear modulus [math]G[/math] and the Poisson ratio [math]\nu[/math], [math]\; m_v = \Large\frac{1-2 \nu}{2 G (1-\nu)}\normalsize .[/math]
Eq. (2) can be rewritten after some manipulation as a differential equation from which the pore pressure [math]p(z,t)[/math] can be solved:
[math]\Large\frac{\partial p}{\partial t}\normalsize = c_s \Large\frac{\partial \sigma}{\partial t}\normalsize + c_v \Large\frac{\partial^2 p}{\partial z^2}\normalsize , \quad c_s = \Large\frac{1}{1+m}\normalsize , \quad c_v = \Large\frac{k \beta}{\rho g n}\frac{m}{1+m}\normalsize , \qquad m = 2 n \Large\frac{G}{\beta}\frac{1-\nu}{1-2 \nu}\normalsize . \qquad (3)[/math]
The total stress [math]\sigma[/math] is the pressure transmitted by the surface wave to the pore fluid and can be approximated by [math]\sigma \approx p_0 \exp(-2 \pi z / L) \cos(2 \pi t /T)[/math], where [math]z[/math] is the depth below the seafloor. The solution of Eq. (3) for a homogeneous soil layer of very large (infinite) depth is (assuming [math]L^2 \gt \gt 2 \pi c_v T[/math])
[math]p(x,z,t) \approx p_0 \Bigg[ \large\frac{1}{1+m}\normalsize e^{- 2\pi \large \frac{z}{L}\normalsize} \cos \Big( 2 \pi (\large\frac{x}{L}-\frac{t}{T}\normalsize)\Big) + \large\frac{m}{1+m}\normalsize e^{-\Large\frac{z}{d}\normalsize} \cos \Big( 2 \pi (\large\frac{x}{L}-\frac{t}{T}+\frac{z}{d}\normalsize)\Big) \Bigg] .\qquad (4)[/math]
The depth [math]d[/math] is given by
[math]d = \Big( \Large\frac{T \, k \, \beta \, m}{\pi \, \rho \, n \, g \, (1+m)}\normalsize \Big)^{1/2} . \qquad (5)[/math]
Substitution of the values of the numerical illustration gives [math]d \approx[/math] 70 cm. Over the top 10 cm the second term in the r.h.s. of Eq. (4) dominates with respect to the first term. Over this depth, wave-induced pressure fluctuations are substantial and is the soil susceptible to transient liquefaction.
For more densely packed soil, the values of the shear modulus are larger and the values of the Poisson ratio are smaller. In this case the first term in the r.h.s. of Eq. (4) dominates. The wave-induced pressure fluctuations penetrate to greater depth into the soil, but the soil is less susceptible to liquefaction.
For liquefaction, the pressure gradient near the soil surface must be larger than the submerged weight of the soil grains. The pressure gradient at [math]z=0[/math] depends mainly on the second term in the r.h.s. of Eq. (4) for the soil characteristics considered. This condition reads
[math]\Large\frac{m}{1+m}\frac{p_0}{d}\normalsize \gt g (\rho_{soil} - \rho) . \qquad (4)[/math]
In the numerical example, liquefaction occurs if the wave height exceeds 4.5 m.
Residual liquefaction
For transient liquefaction it has been assumed that the volumetric soil strain [math]\epsilon[/math] under wave loading is cyclic. According to the soil mechanics theory of Therzagi (1925[13]), the strain [math]\epsilon[/math] gradually increases. We assume for simplicity that the total stress [math]\sigma[/math] increases throughout the soil in proportion to the number [math]N[/math] of wave cycles,
[math]\sigma \propto N \, p_0 \quad[/math] or [math]\quad \Large\frac{d \sigma}{dt}\normalsize \propto \Large\frac{p_0}{T}\normalsize[/math].
Instead of Eq. (3) we now have the following equation for the wave-averaged pore pressure [math]\overline{p}(z,t)[/math] :
[math]\Large\frac{\partial \overline{p}}{\partial t}\normalsize= B \Large\frac{p_0}{T} + c_v \Large\frac{\partial^2 \overline{p}}{\partial x^2}\normalsize , \qquad (5)[/math]
where [math]B[/math] is a proportionality constant dependent on the soil characteristics, that must be determined experimentally. An approximate solution of Eq. (5) can be found by assuming a parabolic depth dependence of the pore pressure for a homogeneous soil layer of thickness [math]D[/math] [14]. The boundary conditions are: for [math]z=0: \; \overline{p}(z,t)=0 \;[/math] and for [math] \; z=D: \; \Large\frac{\partial \overline{p}}{\partial z}\normalsize =0 \;[/math]. The solution is
[math]\overline{p}(z,t) = z(2D-z)\Large\frac{B p_0}{2 c_v T}\normalsize \Big[ 1 - e^{-\Large\frac{3 c_v t}{D^2}}\normalsize \Big] . \qquad (6)[/math]
The dimensionless coefficient [math]B[/math] represents the rate of pore pressure increase per unit applied maximum pressure load in one wave cycle due to soil compaction. For loosely packed soil this rate is of the order [math]B \approx 10^{-3}[/math]; for densely packed soil [math]B[/math] is much smaller[14]. The coefficient [math]B[/math] has been assumed constant in Eq. (5), but in reality it will gradually decrease during soil compaction. The formula (6) therefore overestimates the real value of the pore pressure.
References
- ↑ de Groot, M. B., Bolton, M. D., Foray P., Meijers, P., Palmer, A. C., Sandven, R., Sawicki, A. and The, T. C. 2006 Physics of Liquefaction Phenomena around Marine Structures. Journal of Waterway, Port, Coastal, and Ocean Engineering 132: 227-243
- ↑ Klammler, H., Penko, A.M., Staples, T., Sheremet, A. and Calantoni, J. 2021. Observations and modeling of wave-induced burial and sediment entrainment: Likely importance of degree of liquefaction. Journal of Geophysical Research: Oceans 126, e2021JC017378
- ↑ Anderson, D., Cox, D., Mieras, R., Puleo, J.A. and Hsu, T.-J. 2017. Observations of wave-induced pore pressure gradients and bed level response on a surf zone sandbar. J. Geophys. Res. Oceans 122: 5169– 5193
- ↑ Michallet, H., Mory, M. and Piedra-Cueva, I. 2009. Wave-induced pore pressure measurements near a coastal structure, J. Geophys. Res. 114, C06019
- ↑ 5.0 5.1 Sumer, B.M., Fredsøe, J., Christensen, S. and Lind, M.T. 1999. Sinking or floatation of pipelines and other objects in liquefied soil under waves. Coastal Engineering 38: 53–90
- ↑ Sumer, B.M., Hatipoglu, F., Fredsoe, J. and Sumer, S.K. 2006. The sequence of sediment behaviour during wave-induced liquefaction. Sedimentology 53: 611–629
- ↑ 7.0 7.1 7.2 Sui, T., Kirca, V.S.O, Sumer, B.M., Carstensen, S. and Fuhrman, D.R. 2022. Wave-induced liquefaction in a silt and seashell mixture. Coastal Engineering 178, 104215
- ↑ Gratchev, I.B., Sassa, K., Osipov, V.I. and Sokolov, V.N. 2006. The liquefaction of clayey soils under cyclic loading. Eng. Geol. 86: 70–84
- ↑ Zang, J., Jiang, Q., Jeng, D., Zhang, C., Chen, X. and Wang, L. 2020. Experimental Study on Mechanism of Wave-Induced Liquefaction of Sand-Clay Seabed. J. Mar. Sci. Eng. 8, 66
- ↑ Kirca, V., Sumer, B.M. and Fredsøe, J. 2014. Influence of clay content on wave-induced liquefaction, J. Waterw. Port Coast. Ocean Eng. ASCE 140, 04014024
- ↑ Chavez, V., Mendoza, E., Silva, R., Silva, A. and Losada, M.A. 2017. An experimental method to verify the failure of coastal structures by wave induced liquefaction of clayey soils. Coastal Engineering 123: 1–10
- ↑ Van der Meer, J. and Sigurdarson, S. 2017. Design and construction of berm breakwaters. Advanced Series on Ocean Engineering vol. 40, World Scientific Publ. Co., Singapore
- ↑ Terzaghi, K. 1925. Principles of Soil Mechanics: IV—Settlement and consolidation of clay. Engineering News-Record 95(22): 874-878
- ↑ 14.0 14.1 Verruijt, A. 2006. Offshore soil mechanics. Delft University Lecture Notes
Please note that others may also have edited the contents of this article.
|