Difference between revisions of "Diffraction"
Dronkers J (talk | contribs) |
Dronkers J (talk | contribs) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | |||
| + | |||
{{Review | {{Review | ||
|name=Franciso Taveira Pinto | |name=Franciso Taveira Pinto | ||
| Line 7: | Line 9: | ||
{{ | {{ | ||
Definition|title=Diffraction | Definition|title=Diffraction | ||
| − | |definition= Process by which wave energy is transmitted | + | |definition= Process by which wave energy is transmitted and radiated when the wave is bending around an obstacle such as an island or a breakwater in order to propagate into the sheltered region. }} |
| − | |||
==Notes== | ==Notes== | ||
| Line 17: | Line 18: | ||
The theoretical derivation of the wave diffraction pattern is generally not simple because wave conditions at the boundaries of the obstacle have to be taken into account, as well as conditions at the boundaries of the area in which waves are propagating and the effects of bathymetric wave refraction and wave transformation in shallow water. Design studies of breakwaters or other structures in nearshore waters make generally use of physical scale models or numerical models for determining the wave diffraction pattern. | The theoretical derivation of the wave diffraction pattern is generally not simple because wave conditions at the boundaries of the obstacle have to be taken into account, as well as conditions at the boundaries of the area in which waves are propagating and the effects of bathymetric wave refraction and wave transformation in shallow water. Design studies of breakwaters or other structures in nearshore waters make generally use of physical scale models or numerical models for determining the wave diffraction pattern. | ||
| − | A theoretical derivation of wave diffraction around simple structures in the ideal case of small shallow-water waves in areas of uniform depth (applying linear wave theory) has been given by Penney and Price (1952)<ref> Penny, W.G. and Price, A.T. 1952. The Diffraction Theory of Sea Waves by Breakwater and the Shelter Afforded by Breakwaters. Philos. Trans. Royal Soc. A vol. 244: 253-263</ref>. | + | A theoretical derivation of wave diffraction around simple structures in the ideal case of small shallow-water waves in areas of uniform depth (applying linear wave theory) has been given by Penney and Price (1952)<ref name=PP52> Penny, W.G. and Price, A.T. 1952. The Diffraction Theory of Sea Waves by Breakwater and the Shelter Afforded by Breakwaters. Philos. Trans. Royal Soc. A vol. 244: 253-263</ref>. The analytical solution for diffraction behind a semi-infinite breakwater is shown in Fig. 1. A satellite of wave diffraction at a harbor jetty is shown in Fig. 2 for comparison. |
| + | |||
| + | |||
| + | |||
| + | {| border="0" align="center" | ||
| + | |- | ||
| + | | valign="top"| | ||
| + | [[File:BreakwaterDiffraction.jpg|thumb|350px|left|Fig. 1. Analytical solution of the diffraction of a linear water wave propagating over uniform depth in <math>y</math>-direction behind a rigid breakwater extending from <math>x=-\infty</math> to <math>0</math>. Blue curves are wavefronts and red curves are lines of equal wave height. Adapted after <ref name=PP52/>.]] | ||
| + | | valign="top"| | ||
| + | [[File:WaveDiffraction.jpg|thumb|400px|left|Wave diffraction around the tip of a breakwater. Image Google Earth.]] | ||
| + | |} | ||
==See also== | ==See also== | ||
| − | |||
# [[Wave transformation]] | # [[Wave transformation]] | ||
# [[Shallow-water wave theory]] | # [[Shallow-water wave theory]] | ||
| Line 29: | Line 39: | ||
==References== | ==References== | ||
<references/> | <references/> | ||
| + | |||
| + | |||
| + | [[Category:Definitions]] | ||
| + | [[Category:Physical coastal and marine processes]] | ||
Latest revision as of 09:46, 18 September 2022
Definition of Diffraction:
Process by which wave energy is transmitted and radiated when the wave is bending around an obstacle such as an island or a breakwater in order to propagate into the sheltered region.
This is the common definition for Diffraction, other definitions can be discussed in the article
|
Notes
Wave diffraction at an obstacle illustrates Huygens' principle, which states that every point of a wavefront is a source of waves radiating from this point. This principle holds for all types of wave propagation, including water waves. In this view, wave propagation into a semi-closed area is the interference sum of all the waves that propagate radially from a wave front at the open boundary into this area.
The theoretical derivation of the wave diffraction pattern is generally not simple because wave conditions at the boundaries of the obstacle have to be taken into account, as well as conditions at the boundaries of the area in which waves are propagating and the effects of bathymetric wave refraction and wave transformation in shallow water. Design studies of breakwaters or other structures in nearshore waters make generally use of physical scale models or numerical models for determining the wave diffraction pattern.
A theoretical derivation of wave diffraction around simple structures in the ideal case of small shallow-water waves in areas of uniform depth (applying linear wave theory) has been given by Penney and Price (1952)[1]. The analytical solution for diffraction behind a semi-infinite breakwater is shown in Fig. 1. A satellite of wave diffraction at a harbor jetty is shown in Fig. 2 for comparison.
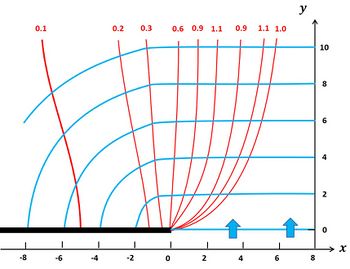 Fig. 1. Analytical solution of the diffraction of a linear water wave propagating over uniform depth in [math]y[/math]-direction behind a rigid breakwater extending from [math]x=-\infty[/math] to [math]0[/math]. Blue curves are wavefronts and red curves are lines of equal wave height. Adapted after [1]. |
See also
