Stability models

Stability: concepts.

The concepts of equilibrium and stability come from Classical Mechanics. A state where a system is in balance with the external forcing so that it does not change in time is called an equilibrium position. However, any equilibrium position may be either stable or unstable. If released near a stable equilibrium position, the system will evolve towards such a position. On the contrary, if released near an unstable equilibrium position, it will go far away from this position. For instance, a pendulum has two equilibrium positions, one up (A), another down (B). If released at rest at any position (except at A) the pendulum will start to oscillate (if it is not already in B) and due to friction it will end up at rest at B. Thus, the pendulum will move spontaneously towards the stable equilibrium and far away from the unstable equilibrium.

Similarly, a beach under constant wave forcing is commonly assumed to reach after some time certain equilibrium profile. However, two main assumptions are here involved: i) an equilibrium state exists and ii) the equilibrium is stable. The existence of an equilibrium profile seems to be granted in the books on coastal sciences and the stability of such an equilibrium is implicitly assumed. However, even if an equilibrium profile exists, it is not necessarily stable. This means that the system would ignore such an equilibrium, it would never tend spontaneously to it. Furthermore, several equilibria may exist, some of them stable, some others unstable.

Example:

Let us assume a system which is described by only one variable as a function of time, [math]x(t)[/math], and two constant parameters [math] \alpha [/math] and [math] x_c \gt 0 [/math] which are representative of both the characteristics of the system and the external forcing. Assume that this variable is governed by the ordinary differential equation:

[math] \frac{dx}{dt} = \alpha (x-x_c)x [/math]

For instance, in a coastal system, [math] \alpha [/math] could represent sediment grain size or wave height, and [math]x(t)[/math] the shoreline displacement at an alongshore location. Given an initial position [math] x(0)=x_0 [/math], the subsequent evolution of the system is described by the solution of the differential equation

[math] x(t) = \frac{x_0 x_c}{x_0 +(x_c-x_0)exp(x_c \alpha t)}[/math]

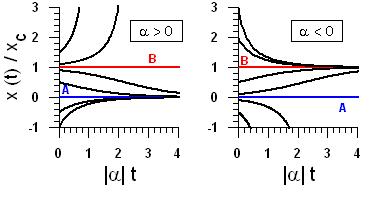
It becomes clear that the system has two equilibrium positions, (A): [math]x=0[/math], and (B): [math]x=x_c[/math]. Moreover, for [math] \alpha \gt 0[/math], (A) is stable while (B) is unstable. In contrast, (A) is unstble and (B) is stable for [math] \alpha \lt 0 [/math]. This is ilustrated by Fig. 1 where typical [math]x(t)[/math] solutions are plotted for various initial conditions.

Fig.1: Left ([math]\alpha\gt 0[/math]), all the solutions starting in a neighborhood of [math]x=0[/math] tend to [math]x=0[/math] for [math]t \to \infty[/math] while there are solutions starting arbitrarily near [math]x=x_c[/math] that do not tend to [math]x=x_c[/math]. Therefore, the equilibrium solution [math]x=0[/math] is stable whereas [math]x=x_c[/math] is unstable. Right ([math]\alpha\lt 0[/math]), all the solutions starting in a neighborhood of [math]x=x_c[/math] tend to [math]x=x_c[/math] for [math]t \to \infty[/math] while there are solutions starting arbitrarily near [math]x=x_c[/math] that do not tend to [math]x=x_c[/math]. Therefore, the equilibrium solution [math]x=x_c[/math] is now stable whereas [math]x=0[/math] has become unstable.

Stability methods: use in coastal sciences.

Coastal and Geomorphic systems exhibit patterns both in space and time. Some of these patterns directly obey similar patterns in the external forcing. For example, a beach profile may erode and subsequently recover directly in response to the cicle storm/calm weather in the external wave forcing with the same time scale. This is known as forced behaviour. Other patterns, even if they are driven by some external forcing, do not resemble similar patterns in the forcing. For instance, although bed ripples may be originated by a unidirectional current over a sandy bed, there is nothing in the current itself which dictates the shape, the lengthscale or the characteristic growth time of the ripples. The ripples constitute a new pattern which is not present in the forcing. This is called free behaviour or self-organized behaviour. The forced behaviour is much simpler to predict once the forcing is known. In contrast, predicting the free behaviour is typically much more complicated as it involves the complex internal dynamics of the system itself.

Stability methods are the genuine tool to describe, understand and model pattern formation by self-organization. The typical procedure is to start considering an equilibrium of the system where the pattern is absent (for instance, flat bed, in case of ripples). The key point is that small fluctuations or irregularities are always present (a perfect flat bed or an exact unidirectional, uniform and steady current do not exist). Then, if the equilibrium is stable, any initial small perturbation of the equilibrium will dye away in time. Thus, those small fluctuations will not succeed in driving the system far from the equilibrium (the bed will keep approximately flat). However, if the equilibrium is unstable, there will exist initial perturbations that will tend to grow. Among all of them, some will grow faster than others and their characteristics will prevail in the state of the system. In other words, the patterns corresponding to these initially dominant perturbations of the equilibrium will emerge and will explain the occurrence of the observed patterns (the ripples). However, different patterns may emerge during the instability process and the finally dominant one (the one which is observed) may not correspond to the initially dominant.