Testpage3

Tidal Bore dynamics

A tidal bore is the ultimate stage of distortion of a tidal wave that propagates upstream a river. This article describes the processes involved in this ultimate stage of tidal wave deformation and the modelling of these processes. For an introduction to the topic of tidal wave deformation the reader is referred to the article Tidal distortion and tidal basin morphodynamics.

Introduction

Table 1. Estuaries and rivers with substantial tidal bores (bore height of half a meter up to several meters).

Estuary/river name	Maximum tidal range [m]	Tide gauge location	Country
Shannon River	5.6	Shannon	Ireland
Humber,Trent	8.3	Hull	UK
Great Ouse	7.4	King's Lynn
Severn	12	Portishead
Dee	9.8	Flint
Mersey	10	Liverpool
Ribble	10.2	Lytham
Morecambe bay, Nith River, River Kent	10.9	Morecambe
River Eden	10.3	Silloth
Seine	8.5	Honfleur	France
Canal de Carentan	7	Carentan
Baie du Mont Saint Michel – Sélune River	14	Granville
Garonne, Dordogne	6	Bordeaux
Pungue	7	Beira	Mozambique
Qiantang	5	Ganpu	China
Indus	4	Port Muhammad Bin Qasim	Pakistan
Hooghly	5.7	Sagar Island	India
Brahmaputra	5.7	Chittagong	Bangladesh
Sittaung	6.3	Moulmein	Myanmar
Batang Lupar River	5.6	Kuching	Sarawak
Kampar River	5.3	Pulo Muda	Sumatra
Hooghly	5.7	Sagar Island	India
Fly , Bamu, Turamu Rivers	4.2	estuary	West Papua
Styx	6.4	Mackay, Queensland	Australia
Daly River	7.9	estuary
Turnagain Arm, Knick Arm	7.9	Anchorage	Alaska
Bay of Fundy, Petitcodiac and Salmon rivers	16	Truro	Canada
Colorado River	7.7	San Filipe	Mexico
Amazon, Araguira, Guama, Capim and Mearim Rivers	3.4	Macapa	Brazil

When a tidal wave propagates upstream into an estuary its shape is progressively distorted. If the mean channel depth [math]D_0[/math] is not much greater than the spring tidal range a (same order of magnitude or a few times larger) and if the intertidal area is smaller than the tidal channel surface area, the high-water (HW) wave crest will propagate faster into the estuary than the low-water (LW) wave trough. The tidal rise period is shortened and the tidal wave is becoming steeper. If the tidal wave can propagate sufficiently far upstream the river without strong damping, the tidal wave front may become so steep that tidal rise corresponds to a water level jump – a so-called tidal bore.

Table 1 gives an overview of estuaries and tidal rivers in which significant tidal bores have been observed. It can be concluded from the table that tidal bores often occur in megatidal zones - areas where the maximum tidal range is greater than 6 m. However, it appears that substantial tidal bores can also occur in areas where the tidal range is smaller, although this is the exception rather than the rule. This exception seems to be limited to tropical and subtropical countries. Rivers are generally shallower in these regions due to abundant supply of fine sediments. Another possible reason is the relative importance of K1 and O2 diurnal tidal components, which can combine with the semidiurnal M2 tide to yield persistent tidal asymmetry (see also the article Ocean and shelf tides). However, for the rivers listed in Table 1 this does not seem to play an important role .

Engineering works (weirs, dredging) during the past century have weakened or even completely suppressed tidal bores in many rivers, for example in the rivers Seine, Loire, Charente and Petitcodiac.

Illustrations of tidal bores are shown in Fig. 1.

Tidal bore formation

The analysis of nonlinear tidal wave transformation in estuaries, in terms of tidal forcing at the estuary mouth and large-scale geometrical properties of the channel, has received considerable attention (see Tidal distortion and tidal basin morphodynamics). By contrast, the extreme nonlinear tidal-wave case where tidal bores form is much less studied.

The formation of tidal bores is mainly governed by the progressive distortion of the tidal wave as it propagates up the estuary. This extreme nonlinear deformation of the tidal wave occurs under special conditions, in particular :

• a large tidal amplitude [math]a[/math],
• a long, shallow and convergent channel.

River flow and river-bed slope also influence tidal bore formation. River flow contributes to tidal wave deformation by enhancing the longitudinal velocity gradient and river-bed slope by upstream reduction of the water depth. However, river flow and river-bed slope also contribute to tidal wave damping and thus oppose tidal bore formation . The latter effect usually dominates. Observations show that the tidal bore in the Garonne and Dordogne (France) is suppressed at high river runoff. A similar effect is observed in the Daly estuary by Wolanski et al. (2006), who relate the occurrence of the tidal bore at low river discharge to the small water depth during such conditions. The opposite effect is reported for the Guamá-Capim river system near the mouth of the Amazon River, where tidal bores are observed only at high river discharges, in conjunction with high equinoctial tides.

Figure 1. Many natural estuaries have large shoals in the mouth zone. These so-called mouth bars strongly enhance distortion of the tidal wave entering the estuary. Left image: Tidal bore in the Seine River around 1960, before the mouth bar was dredged. Right image: Tidal bore in the Qiangtang estuary, where a large mouth bar is still present (https://en.wikipedia.org/wiki/Qiantang_River ).

Although most studies of tidal bore formation have focused on estuary-river systems with gradual bed slopes, there is strong evidence that steep gradients in the mean depth may induce tidal bore formation. This phenomenon is well known for tsunami waves propagating onto the shoreface or for swell waves collapsing on the beach. Observations show that tidal bores often develop in shallow rivers that discharge from the higher upstream zone into a broad estuary. If the tidal wave has already acquired sufficient asymmetry when travelling through the estuary, a tidal bore develops when the tidal wave surges into the shallow river. The different stages of tidal bore formation are sketched in Fig. 2 . In this case river discharge is favorable to tidal bore development. Fig. 3 shows the sharp increase in the current velocity and suspended sediment concentration recorded in the megatidal Baie du Mont Saint Michel at spring tide when the tidal flood wave enters the tidal flat area of the landward inner basin.

Figure 2. Left panels, 1-4. Schematic representation of successive stages of tidal bore development when the tidal flood wave propagates from a tidal basin into a shallow upstream intertidal area. Adapted from Lynch(1982) . Right panel: Tidal bore spilling over the intertidal mudflats of the megatidal Morecambe bay. Photo credit Arnold Price.

Figure 3. Tide elevation [math]\small \zeta[/math] (above the dry bed), current velocity [math]\small u[/math] and suspended sediment concentration [math]\small c[/math] during springtide on a tidal flat in the Baie du Mont Saint Michel. The measurements started when the tidal flat at the measuring station was (almost) dry, just before the tidal bore spilled over the tidal flat. A rapid rise of the current velocity was recorded when the bore arrived. The suspended sediment concentration (mainly fine silty sand) peaked sharply at the passage of the bore front and quickly felt down afterwards. During the remaining flood period and during ebb the suspended sediment concentrations were much lower. The measurements illustrate the strong bottom stirring and sediment resuspension produced by the turbulent bore front, which significantly contributes to landward sediment transport and tidal basin infill . A video of the arrival of the tidal bore can be viewed by clicking here. The photo at the right is a still from the video.

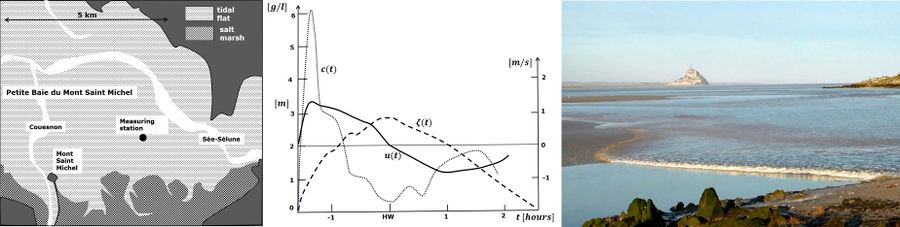
Propagation of tidal bores

Figure 4: Schematic representation of a hydraulic jump propagating with velocity [math]c[/math] in a moving frame. In this frame moving with velocity [math]c[/math] the hydraulic jump appears stationary; time derivatives are zero. The corresponding mass and momentum balance equations from which the propagation characteristics can be derived are indicated in the figure. The symbols used stand for: [math]u[/math]= flow velocity in a fixed frame, [math]v[/math]= flow velocity in the moving frame, [math]D[/math]= water depth, [math]g[/math]=gravitational acceleration; subscripts 1 and 2 indicate upstream and downstream conditions, respectively.

Nonlinear processes become increasingly important in the final stages of bore development. These processes can no longer be analyzed with analytical methods, but only with numerical simulation models. The hydrostatic long-wave equations no longer apply to describe the emergence of a breaking tidal wave. Non-hydrostatic effects must be taken into consideration. This will be discussed further in the next sections.

A bore is a propagating transition between two streams of water depths [math]D_1[/math] and [math]D_2[/math] with speed [math]c=(D_2u_2-D_1u_1)/ (D_2-D_1)[/math], where [math]D_1 \lt D_2[/math]. Once such a hydraulic jump has developed, its propagation characteristics can be derived from the mass and momentum balance equations, see Fig. 4. By eliminating [math]v_1=c-u_1[/math] or [math]v_2=c-u_2[/math] from these equations two equivalent expressions can be derived for the height of the tidal bore:

[math]\Delta D= \Large \frac{D_1}{2} [\normalsize -3 + \sqrt{1 + 8 F_1^2} \Large ] \normalsize = \Large \frac{D_2}{2} [\normalsize 3 - \sqrt{1 + 8 F_2^2} \Large ] \normalsize, \quad \quad (1)[/math]

where [math]\Delta D=D_1 -D_2[/math] is the bore height and the Froude numbers are given by

[math]F_1^2 = \Large \frac{v_1^2}{g D_1}\normalsize = \large \frac{D_2 (D_1+D_2)}{2 D_1^2} \normalsize , \quad F_2^2 = \Large \frac{v_2^2}{g D_2}\normalsize = \large \frac{D_1 (D_2+D_1)}{2 D_2^2} \normalsize . \quad \quad (2)[/math]

For [math]\Delta D\lt 0.4 h_2[/math] the tidal bore propagation speed [math]c[/math] can be fairly well represented by

[math]c \approx \Large \frac{1}{2} \normalsize (c_1 + c_2) , \quad \quad (3)[/math]

where [math] c_1 = u_1 + \sqrt{g D_1} , \quad c_2 = u_2 + \sqrt{g D_2}[/math].

If the bore velocity [math] c [/math] is equal to [math]c_2[/math] (i.e. [math]F_2 = 1[/math]) the bore height [math] \Delta D[/math] is zero. Another requirement for a tidal bore is therefore [math]c \lt c_2[/math] or [math]F_2 \lt 1[/math] and [math]F_1 \gt 1[/math]. Because [math]c_2[/math] is the propagation speed of long-wave disturbances upstream of the bore, these disturbances (undulations) will catch up to the bore. A slowly propagating bore ([math]F_2 \lt \lt 1[/math]) will thus grow faster and become higher than a fast propagating bore ([math]F_1, F_2 [/math] close to 1) .

Tidal bore characteristics

In the previous section the tidal bore is represented by a hydraulic jump separating upstream and downstream regions of constant water depth. This simplification ignores the fact that energy loss occurs in the transition zone. Conservation of mass and momentum at the transition does not imply conservation of energy; there is a positive energy head loss

[math]\Delta E = \rho g \Delta H = \rho g \Delta D + 0.5 \rho (v_2^2 -v_1^2) , \quad \quad (6)[/math]

where [math]\rho[/math] is the density of water.

Two forms of energy dissipation occur at the transition, leading to two different types of bores.

Undular bores

For [math]F_1[/math] smaller than approximately 1.3, the bore transition is smooth and followed by a wave train (Fig. 5). The bore then consists of a mean jump between two water depths on which secondary waves are superimposed. This type of bore is usually called an undular bore. Favre (1935) was the first to describe this phenomenon from laboratory experiments. That is why undular bores are sometimes referred to as Favre waves.

Figure 5. Left image: Undular tidal bore on the Garonne River (Bonneton et al. 2011 ). Right image: Tidal bore refraction around an island of the Garonne River. From Bonneton et al. 2011.

The propagation speed of short waves upstream of the bore is, according to linear shallow-water wave theory

[math] c_w = u_2 + \sqrt{\Large \frac{g}{k}\normalsize \tanh(kD_2)} \approx u_2 + \sqrt{gD_2 (1- \frac{k^2 D_2^2}{3})} , \quad \quad (4)[/math]

where [math]k=2 \pi / \lambda[/math] is the wave number and [math]\lambda[/math] the wavelength. The latter approximation holds only if [math]kD_2 \le 1[/math]. Such short waves are stationary in a frame moving with the bore front if [math]c_w – u_2 = v_2[/math]. This equality provides an estimate of the wavelength of these waves that follow the bore front,

[math]\lambda \approx \Large \frac{2 \pi }{\sqrt{3}}\normalsize D_2 (1-F_2^2)^{-1/2} . \quad \quad (5)[/math]

In undular bores energy, is dissipated by the wave train following the bore front. The energy flux per unit width radiated by the wave field can be approximated by [math]P=0.5 \rho g c_g a^2[/math], where [math]a[/math] is the wave amplitude and [math]c_g[/math] the wave group velocity in the moving frame following the bore front (see shallow-water wave theory). The wave group velocity [math]c_g[/math] is given by

[math]c_g = u_2 + n (c - u_2) - c = v_2 \; (1-n), \quad n=\large (\frac{1}{2}+ \frac{kD_2}{\sinh(2kD_2)}) \normalsize . \quad \quad (7)[/math]

Lemoine (1948) equated this energy flux with the flux of energy corresponding to the energy head loss (Eq. 6), [math]P= D_2 v_2 \Delta E[/math], to obtain an estimate for the wave amplitude [math]a[/math] as a function of [math]D_1[/math] and [math]D_2[/math]. As this approach ignores wave-induced mass transport it is valid only for very small bores ([math]F_1[/math] close to 1).

Figure 6. Tidal wave distortion and bore formation observed in the Gironde-Garonne estuary (Bonneton et al. 2015) at spring tide. Tidal bore illustrations at Podensac field site, located 126 km upstream the river mouth.

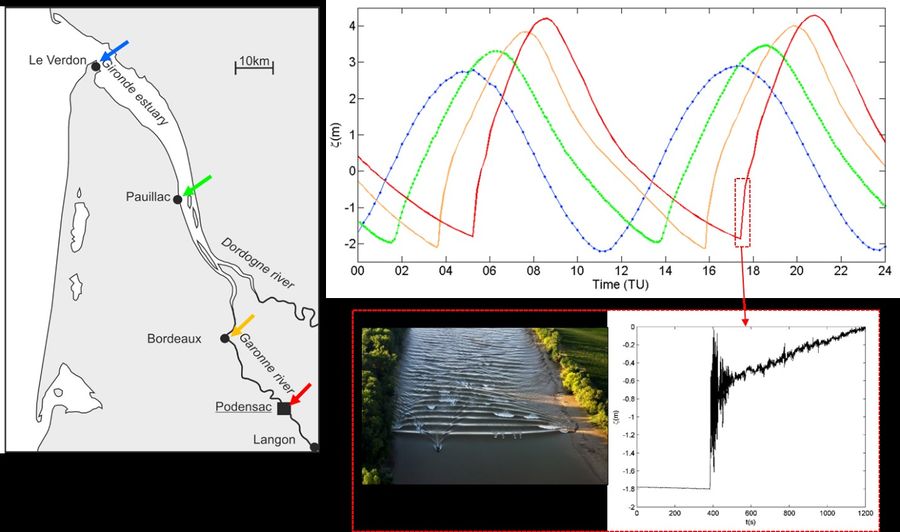
Breaking bores

For large [math]F_1[/math], bores correspond to turbulent breaking fronts (figures 1 and 2), where the energy head loss is dissipated by turbulent eddies. The transition between undular and turbulent bores is shown in figure 9. The turbulent eddies exert strong shear stresses on the channel bed, causing high concentrations of suspended sediment, see Fig. 3. Turbulent bores contribute significantly to upstream sediment transport.

Figure 7. Left image: Tidal bore in the Petitcodiac River, which is undular at the middle of the channel and breaking near the channel banks. Right image: Breaking tidal bore in the Kampar River, Sumatra.

In many estuaries and tidal rivers the bore propagation near the shallow channel banks differs from the bore propagation in the deeper middle part of the channel. The Froude number [math]F_1[/math] is relatively lower at the deeper parts of the channel, where the bore has often an undulating character, while a higher breaking bore occurs in the shallower parts. This phenomenon is illustrated in Fig. 7 for the tidal bore in the Petitcodiac River. In the next section the interaction between different propagation characteristics at the channel centre and the channel banks will be discussed more in detail.

Dispersive tidal bores

Even in the absence of strong bathymetric gradients cross-sectional depth variations can significantly influence tidal bore properties . Most laboratory, theoretical and numerical bore studies have not considered transverse variations of the channel bed. However, natural estuary and river channels are non-rectangular and present most of the time a variable cross-section with a nearly trapezoidal shape and gently sloping banks.

File:DispersiveOndularBores.jpg

Figure 8. Illustration of the transition between dispersive and dispersive-like undular bore regimes (Chassagne et al. 2019).

The propagation of undular bores over channels with variable cross-sections was studied by Treske (1994) in the lab and by Bonneton et al. (2015) in the field. Both studies identified a transition around [math] F_t=1.15[/math]. For [math]F_1 \gt F_t[/math] the secondary wave field in the mid channel is very similar to Favre waves. For [math]F_1 \lt F_t[/math], the secondary wave wavelength in the whole channel is at least two to three times larger than in a rectangular channel for the same Froude numbers. It was shown that this new undular bore regime (Fig. 8 c,d) differs significantly from classical dispersive undular bores in rectangular channels (i.e. Favre waves). Chassagne et al. (2019) recently showed that this undular bore regime (named “dispersive-like bore”) is controlled by hydrostatic non-dispersive wave properties, with a dynamics similar to edge-waves in the near-shore. The transition between dispersive and dispersive-like bores is illustrated on Fig. 8.

Modelling

Tidal bore formation involves a large range of temporal and spatial scales, from the estuary to the turbulence scale. For this reason it is difficult to model these processes as a whole, both from physical models (laboratory experiments) and numerical approaches.

Physical models

Figure 9. Experimental study of undular bores (Favre-waves) in open rectangular channels (Treske 1994<name=Tr></ref>). Undular bores, Fr=1.2 and 1.3; transition to a turbulent bore, Fr=1.35; turbulent bore, Fr=1.45.

Due to the large range of scales, it is impossible to design a tidal bore laboratory experiment in close similitude with natural tidal bores. However, leaving aside the tidal wave transformation and bore formation, the bore in itself (i.e. hydraulic jump in translation) can be studied in detail from flume experiments. The bore is commonly generated in a rectangular flume by using a fast-closing gate at the upstream end of the flume. This method allows the study of the different bore regimes (see Fig. 9) and provides valuable insights in secondary wave structure and vortical motions.

To avoid the abrupt bore generation of the above method, Rousseaux et al. (2016) proposed a novel approach. This method mimics the tidal asymmetry met in nature between the ebb and the flood. Fig. 10 shows an example of a tidal-like bore generated with this method.

Figure 10. Experimental study of tidal-like bore using a laser sheet and fluorescent dye (Rousseaux et al. 2016).

Numerical models

The secondary waves associated with undular bores have dispersive properties and thus cannot be described by the nonlinear shallow-water (NSW) equations, which hold for long-wave phenomena (such as tidal motion) and assume hydrostatic pressure. The basic theoretical approach for undular tidal bores is based on weakly dispersive Boussinesq-type equations . Weakly dispersive Boussinesq-type equations are an extension of the NSW equations by including terms that take into account vertical fluid accelerations, see Boussinesq equations.

The properties of breaking turbulent bores, on the contrary, are quite well described by the non-dispersive NSW equations with jump conditions .

Figure 11. Large Eddy Simulation of turbulence generated by a weak breaking bore. Streamlines indicate recirculation structures under the bore (Lubin et al. 2010).

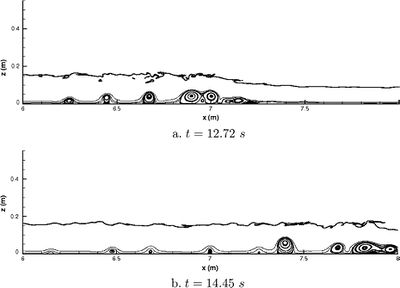
Recent approaches, based on the resolution of the general Navier Stokes equations in their multiphase form (water phase and air phase), allow a detailed description of bore structure, turbulence and air entrainment in a roller at the bore front. Figure 11 presents the simulation of recirculating structures under a breaking bore. Navier-Stokes approaches are dedicated to small scale bore processes that cannot be applied to tidal bores at the estuarine scales because of limited computation power. Such applications would require long-wave models, where small scale vorticity motions are parametrized and not directly resolved.

The most common long-wave description is the Saint Venant or Nonlinear Shallow Water (NLSW) model. This model gives a good description of the large-scale tidal wave transformation. However, the onset of a tidal bore and its evolution upstream is controlled by non-hydrostatic dispersive mechanisms. If the onset of the tidal bore can be well described by classical weakly dispersive weakly nonlinear Boussinesq-type equations, the subsequent nonlinear evolution, for high-intensity tidal bores, requires the use of the basic fully nonlinear Boussinesq equations, named Serre-Green Naghdi (SGN) equations. This modelling approach allows an accurate description of both, the tidal bore formation at the estuarine scale and the bore structure at the local scale (Fig. 12).

Figure 12. Left image: Computed tidal wave distortion and bore formation in a convergent estuary with uniform depth. The figures shows the spatial tidal wave structure at successive times of a Serre-Green Naghdi simulation. From Filippini et al. 2019. Right image: Serre-Green Naghdi simulation of an undular bore. Comparisons between experimental data (at 6 gauges, Fr=1.104) from Soares-Frazao and Zech (2002) and model prediction (Tissier et al. 2011).

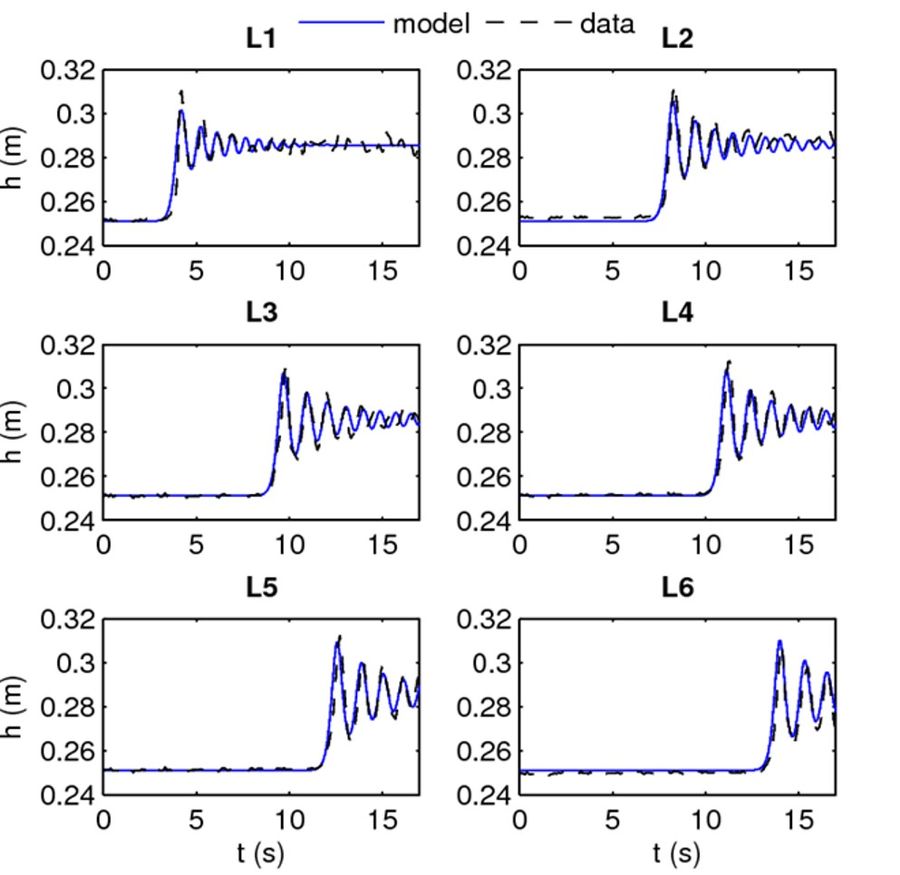
Further reading

Bartsch-Winkler, S., and Lynch, D. K. 1988. Catalog of worldwide tidal bore occurrences and characteristics. US Government Printing Office.

Colas, A. 2017. Mascaret, prodige de la marée. Atlantica Editions.

Dronkers, J.J. 1964. Tidal computations in rivers and coastal waters. North-Holland Publ. Co., 518 pp.

References

The main authors of this article are Philippe Bonneton and Job Dronkers Please note that others may also have edited the contents of this article. Citation: Philippe Bonneton; Job Dronkers; (2019): Testpage3. Available from http://www.coastalwiki.org/wiki/Testpage3 [accessed on 21-11-2024] For other articles by this author see Category:Articles by Philippe Bonneton For other articles by this author see Category:Articles by Job Dronkers For an overview of contributions by this author see Special:Contributions/Bonneton P For an overview of contributions by this author see Special:Contributions/Dronkers J