Modelling coastal hydrodynamics

Introduction

In the analysis of the coastal hydrodynamic processes, modelling (physical, numerical and composite) is often employed to simulate the main phenomena in the coastal region. Physical models (PM) refer to the use of laboratory models at an appropriate scale ( micro, small, medium and large scale models ) for investigating the relevant process, numerical models (NM) refer to the use of computer codes (commercial, open source, home-made software) and composite models (CM) refer to the integrated and balanced use of physical and numerical models. Hydrodynamic modelling forms the basis for many other modelling studies, whether sediment transport, morphology, waves, water quality and/or ecological changes are being investigated. Research is being carried out to improve the representation of tides, waves, currents, and surge in coastal waters.
In the following sections a general outline is given initially with the main characteristics of the coastal hydrodynamics and the associated physical, numerical and composite modelling of the main coastal processes. Phenomena, concepts and insights are presented briefly and modelling of coastal hydrodynamics using physical, numerical and composite models is described. Finally practical applications from the three methodologies are presented together with an extensive list of references.

General outline

Coastal Hydrodynamics and Modelling

Coastal Hydrodynamics

The dynamic processes that exist in the nearshore region are generated by a number of different drivers. Under the influence of these external forces, the fluid motion of the water manifests itself as coastal currents, tides and tidal currents, internal and surface waves, storm surges, tsunamis and others (Horikawa, 1988).
The main difference between coastal waters and deep ocean waters is the presence of two physical constraints (i.e., the sea bottom, at a relatively shallow depth, and the coastline) which somehow determine the motion of the sea water.
The nearshore zone is defined as the region extending from a landward limit associated with storm-wave phenomena (e.g., overwash), to a seaward limit beyond the point where incident waves break, but which depends on the specific context (Horikawa, 1988). Within this zone, several other regions may be distinguished, as shown in figure 1 (Horikawa, 1988). The most relevant of these are the breaker zone, the breaking point, and the surf zone. The former is the zone where incident irregular waves break; the breaking point is where breaking begins and the waves attain maximum height, and the surf zone is defined as the region between the seaward limit of the breaker zone and the area of high turbulence created by the collision of the backrushing water mass and the incoming waves (Horikawa, 1988).

Following Sánchez-Arcilla and Lemos (1990) , the relevant phenomena in the surf zone can be classified into four different types:

1. Sediment transport and corresponding changes in morphology, with a characteristic time scale of 1 day to 1 month, and a spatial scale between 100 m and 1000 m,
2. Currents (non-oscillatory flow), with time scales between 10 minutes and 1 hour, and spatial scales similar to those of sediment transport,
3. Organised oscillatory flows (i.e., wind waves, infra-gravity waves), with time scales ranging from 10^-1 sec to 10 min, and space scales from 1 to 100 m.
4. Random oscillatory flow (turbulence), whose length scales are between 10^-3 to 10¹ sec , and with small (10^-4 to 10^-1 m) spatial scales.

In a general overview, it can be said that the main features in coastal hydrodynamics are the wind waves, generated by the stress exerted on the ocean surface by the wind. As these waves travel from deep waters into shallower regions, they become more non-linear and dissipative, transferring energy from the peak of the spectrum to higher and lower frequencies. Eventually, the proximity of the sea bottom will induce the breaking of the waves, producing a severe increase in the marine turbulence level, and generating different types of currents, which may extend beyond the surf zone.
However, the study of nearshore hydrodynamics is not an easy task. Wave, current and turbulence scales tend to overlap, thus giving rise to the interaction (to some degree) of these three flow types; since the individual flows are non-linear in nature, their interaction becomes quite complex. The usual procedure followed to derive and understand the governing equations is to decompose all the state variables into contributions from currents, waves and turbulence, and then use time-averaging operators to isolate the desired phenomenon.

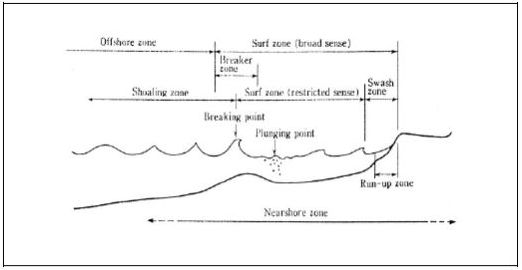
Figure 1: Zone division in the nearshore region (Horikawa 1988)

Physical Modelling

Physical models and laboratory experiments remain part and parcel of the research methodology because of their many strong points, such as:

1. Observability: experiments to investigate mechanisms that are difficult to observe in nature,
2. Measurability: experiments to isolate phenomena that are difficult to measure in nature,
3. Repeatability: repeated experiments, to investigate the range of inherent uncertainty of phenomena,
4. Input control: experiments with various realistic input time series, to assess the predictive capability of numerical models,
5. Process control: experiments for simple situations, in order to validate the results of theoretical behaviour analyses,
6. Overview: experiments concerning spatial pattern formation (wave fields, morphology, etc.) and requiring synoptic measurements,
7. Cost: filling in of field measurements, which are necessarily disperse,
8. Robustness: modelling of processes that cannot be modelled numerically, because (unlike numerical models) physical models are basically similar to prototype (especially in facilities that model processes at full scale).

Facilities of various sizes (from large to micro scale) are available for physical modelling of coastal processes. The size of the facility for use depends on the scale and scope of the phenomenon to be modelled. If the prime interest is in the detail of processes the size of the facility may not be critical but the range of the measuring equipment available may be. If the intention is to model flow-boundary interactions over a large area , a large facility is essential so that model scales of 1:10 or 1:100 can be used. Combining detailed process and scale modelling in different facilities can prove very valuable, nesting the results of process studies of critical zones within those from a less detailed, broader scale model.
Large scale models are desirable since model laws other than Froude scaling (Reynolds, Weber etc) can be considered and the main characteristic parameters can be measured accurately. The scale selection should assure that the dominant forces are well represented. For wave reproduction the capillary forcesshould play an insignificant role only. Consequently, the wave lengths must not be too sort. A practical lower limit is 0.3 m corresponding to a wave period of 0.4 s. Very small scales also affect the repeatability by which the small-scale waves can be reproduced in the laboratory. In tests where viscous effects are important, attention has to be paid to the Reynolds number. This is related primarily to the coastal structure being tested rather than to the ability to reproduce the waves. However, micro-models can be an inexpensive alternative for the hydraulic laboratories of Universities and even medium consultancy firms. They are envisaged as a tool for: the preliminary research of wave-related coastal processes, the development and initial testing of novel ideas, the preliminary design of wave related coastal protection schemes and the testing of alternative design options, the provision of immediate answers and insights to simple coastal engineering problems, the pre-design of large scale physical models.

Physical modelling is more an art than a science when scale and model effects are not taken into account in a physical model . Scale effects are related to the inability to scale all relevant forces from prototype to model scale. Model or laboratory effects are related to the inappropriate set-up of the model and the incorrect reproduction of the governing forces, the boundary conditions, the measurement system and the data analysis. Facilities vary widely and are expensive to install and maintain. The correct facility for the application may not be available.

Numerical Modelling

The rapid development of computing technology has furnished a large number of models to be employed in coastal hydrodynamic problems. A variety of coastal models are available and the modelling techniques have become quite mature . The numerical technique can be based on the finite element method, finite difference method , boundary element method, finite volume method and Eulerian-Lagrangian method. The time-stepping algorithm can be implicit, semi-implicit, explicit, or characteristic-based. The shape function can be of the first order, second order, or a higher order. The modelling can be simplified into different spatial dimensions, i.e., a one-dimensional (1D) model, two-dimensional (2D) depth-integrated model, 2D lateral-integrated model, 2D layered model and 3D model.

An analysis of coastal hydraulics and water quality often demands the application of heuristics and empirical experience, and is accomplished through some simplifications and modelling techniques according to the experience of specialists. However, the accuracy of the prediction is to a great extent dependent on open boundary conditions, model parameters, and the numerical scheme. The adoption of a proper numerical model for a practical coastal problem is a highly specialized task. These predictive tools inevitably involve certain assumptions and/or limitations, and can be applied only by experienced engineers who possess a comprehensive understanding of the problem domain. This leads to severe constraints on the use of models and large gaps in understanding and expectations between the developers and practitioners of a model.

Composite Modelling

Composite Modelling (CM) is defined as the integrated and balanced use of physical and numerical models . Combining physical modelling and numerical modelling, or Composite modelling may open up new opportunities for physical modelling, c.q. lead to a new generation of physical modelling infrastructure.
Several ideas and expectations are associated with CM. Firstly, CM allows to get the best out of both Physical Models (PM) and Numerical Models (NM) for a given problem – apply each for that geographical area or for those scales where it performs best, and so lead to an overall better simulation of the relevant processes. Also it may provide more quality (higher accuracy, reduced uncertainty) against the same cost or it may provide the capabilities to model more complex problems which individual PM or NM cannot.

References

The main author of this article is Prinos, Panayotis Please note that others may also have edited the contents of this article. Citation: Prinos, Panayotis (2012): Modelling coastal hydrodynamics. Available from http://www.coastalwiki.org/wiki/Modelling_coastal_hydrodynamics [accessed on 21-11-2024] For other articles by this author see Category:Articles by Prinos, Panayotis