Modelling coastal hydrodynamics

From Coastal Wiki
Revision as of 11:26, 5 September 2012 by Laura A (talk | contribs)
Jump to: navigation, search

Introduction

In the analysis of the coastal hydrodynamic processes, modelling (physical, numerical and composite) is often employed to simulate the main phenomena in the coastal region. Physical models (PM) refer to the use of laboratory models at an appropriate scale ( micro, small, medium and large scale models ) for investigating the relevant process, numerical models (NM) refer to the use of computer codes (commercial, open source, home-made software) and composite models (CM) refer to the integrated and balanced use of physical and numerical models. Hydrodynamic modelling forms the basis for many other modelling studies, whether sediment transport, morphology, waves, water quality and/or ecological changes are being investigated. Research is being carried out to improve the representation of tides, waves, currents, and surge in coastal waters.
In the following sections a general outline is given initially with the main characteristics of the coastal hydrodynamics and the associated physical, numerical and composite modelling of the main coastal processes. Phenomena, concepts and insights are presented briefly and modelling of coastal hydrodynamics using physical, numerical and composite models is described. Finally practical applications from the three methodologies are presented together with an extensive list of references.


General outline

Coastal Hydrodynamics and Modelling

Coastal Hydrodynamics

The dynamic processes that exist in the nearshore region are generated by a number of different drivers. Under the influence of these external forces, the fluid motion of the water manifests itself as coastal currents, tides and tidal currents, internal and surface waves, storm surges, tsunamis and others (Horikawa, 1988).
The main difference between coastal waters and deep ocean waters is the presence of two physical constraints (i.e., the sea bottom, at a relatively shallow depth, and the coastline) which somehow determine the motion of the sea water.
The nearshore zone is defined as the region extending from a landward limit associated with storm-wave phenomena (e.g., overwash), to a seaward limit beyond the point where incident waves break, but which depends on the specific context (Horikawa, 1988). Within this zone, several other regions may be distinguished, as shown in figure 1 (Horikawa, 1988). The most relevant of these are the breaker zone, the breaking point, and the surf zone. The former is the zone where incident irregular waves break; the breaking point is where breaking begins and the waves attain maximum height, and the surf zone is defined as the region between the seaward limit of the breaker zone and the area of high turbulence created by the collision of the backrushing water mass and the incoming waves (Horikawa, 1988).

Following Sánchez-Arcilla and Lemos (1990) [1], the relevant phenomena in the surf zone can be classified into four different types:

  1. Sediment transport and corresponding changes in morphology, with a characteristic time scale of 1 day to 1 month, and a spatial scale between 100 m and 1000 m,
  2. Currents (non-oscillatory flow), with time scales between 10 minutes and 1 hour, and spatial scales similar to those of sediment transport,
  3. Organised oscillatory flows (i.e., wind waves, infra-gravity waves), with time scales ranging from 10-1 sec to 10 min, and space scales from 1 to 100 m.
  4. Random oscillatory flow (turbulence), whose length scales are between 10-3 to 101 sec , and with small (10-4 to 10-1 m) spatial scales.

In a general overview, it can be said that the main features in coastal hydrodynamics are the wind waves, generated by the stress exerted on the ocean surface by the wind. As these waves travel from deep waters into shallower regions, they become more non-linear and dissipative, transferring energy from the peak of the spectrum to higher and lower frequencies. Eventually, the proximity of the sea bottom will induce the breaking of the waves, producing a severe increase in the marine turbulence level, and generating different types of currents, which may extend beyond the surf zone.
However, the study of nearshore hydrodynamics is not an easy task. Wave, current and turbulence scales tend to overlap, thus giving rise to the interaction (to some degree) of these three flow types; since the individual flows are non-linear in nature, their interaction becomes quite complex. The usual procedure followed to derive and understand the governing equations is to decompose all the state variables into contributions from currents, waves and turbulence, and then use time-averaging operators to isolate the desired phenomenon.


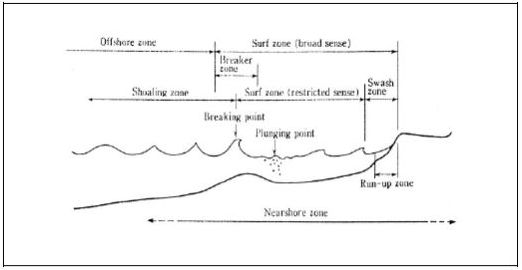
Zone division in the nearshore region .jpg
Figure 1: Zone division in the nearshore region (Horikawa 1988)


Physical Modelling

Physical models and laboratory experiments remain part and parcel of the research methodology because of their many strong points, such as:

  1. Observability: experiments to investigate mechanisms that are difficult to observe in nature,
  2. Measurability: experiments to isolate phenomena that are difficult to measure in nature,
  3. Repeatability: repeated experiments, to investigate the range of inherent uncertainty of phenomena,
  4. Input control: experiments with various realistic input time series, to assess the predictive capability of numerical models,
  5. Process control: experiments for simple situations, in order to validate the results of theoretical behaviour analyses,
  6. Overview: experiments concerning spatial pattern formation (wave fields, morphology, etc.) and requiring synoptic measurements,
  7. Cost: filling in of field measurements, which are necessarily disperse,
  8. Robustness: modelling of processes that cannot be modelled numerically, because (unlike numerical models) physical models are basically similar to prototype (especially in facilities that model processes at full scale).

Facilities of various sizes (from large to micro scale) are available for physical modelling of coastal processes. The size of the facility for use depends on the scale and scope of the phenomenon to be modelled. If the prime interest is in the detail of processes the size of the facility may not be critical but the range of the measuring equipment available may be. If the intention is to model flow-boundary interactions over a large area , a large facility is essential so that model scales of 1:10 or 1:100 can be used. Combining detailed process and scale modelling in different facilities can prove very valuable, nesting the results of process studies of critical zones within those from a less detailed, broader scale model.
Large scale models are desirable since model laws other than Froude scaling (Reynolds, Weber etc) can be considered and the main characteristic parameters can be measured accurately. The scale selection should assure that the dominant forces are well represented. For wave reproduction the capillary forcesshould play an insignificant role only. Consequently, the wave lengths must not be too sort. A practical lower limit is 0.3 m corresponding to a wave period of 0.4 s. Very small scales also affect the repeatability by which the small-scale waves can be reproduced in the laboratory. In tests where viscous effects are important, attention has to be paid to the Reynolds number. This is related primarily to the coastal structure being tested rather than to the ability to reproduce the waves. However, micro-models can be an inexpensive alternative for the hydraulic laboratories of Universities and even medium consultancy firms. They are envisaged as a tool for: the preliminary research of wave-related coastal processes, the development and initial testing of novel ideas, the preliminary design of wave related coastal protection schemes and the testing of alternative design options, the provision of immediate answers and insights to simple coastal engineering problems, the pre-design of large scale physical models.

Physical modelling is more an art than a science when scale and model effects are not taken into account in a physical model [2]. Scale effects are related to the inability to scale all relevant forces from prototype to model scale. Model or laboratory effects are related to the inappropriate set-up of the model and the incorrect reproduction of the governing forces, the boundary conditions, the measurement system and the data analysis. Facilities vary widely and are expensive to install and maintain. The correct facility for the application may not be available.

Numerical Modelling

The rapid development of computing technology has furnished a large number of models to be employed in coastal hydrodynamic problems. A variety of coastal models are available and the modelling techniques have become quite mature [3]. The numerical technique can be based on the finite element method, finite difference method , boundary element method, finite volume method and Eulerian-Lagrangian method. The time-stepping algorithm can be implicit, semi-implicit, explicit, or characteristic-based. The shape function can be of the first order, second order, or a higher order. The modelling can be simplified into different spatial dimensions, i.e., a one-dimensional (1D) model, two-dimensional (2D) depth-integrated model, 2D lateral-integrated model, 2D layered model and 3D model.

An analysis of coastal hydraulics and water quality often demands the application of heuristics and empirical experience, and is accomplished through some simplifications and modelling techniques according to the experience of specialists. However, the accuracy of the prediction is to a great extent dependent on open boundary conditions, model parameters, and the numerical scheme. The adoption of a proper numerical model for a practical coastal problem is a highly specialized task. These predictive tools inevitably involve certain assumptions and/or limitations, and can be applied only by experienced engineers who possess a comprehensive understanding of the problem domain. This leads to severe constraints on the use of models and large gaps in understanding and expectations between the developers and practitioners of a model.

Composite Modelling

Composite Modelling (CM) is defined as the integrated and balanced use of physical and numerical models [4]. Combining physical modelling and numerical modelling, or Composite modelling may open up new opportunities for physical modelling, c.q. lead to a new generation of physical modelling infrastructure.
Several ideas and expectations are associated with CM. Firstly, CM allows to get the best out of both Physical Models (PM) and Numerical Models (NM) for a given problem – apply each for that geographical area or for those scales where it performs best, and so lead to an overall better simulation of the relevant processes. Also it may provide more quality (higher accuracy, reduced uncertainty) against the same cost or it may provide the capabilities to model more complex problems which individual PM or NM cannot.
Several authors have discussed CM, though often with slightly different definitions. Barthel and Funke (1989)[5] referred to it as “hybrid modelling” while Oumeraci (1999)[2] proposes a move towards CM, by combining the main strengths of physical and numerical models within a hydro-informatics style of framework. As part of a CM, physical model tests would be conducted at a large enough scale to minimise the scale effects, and concentrating on important processes that are not well enough understood to be modelled accurately in a numerical model (i.e. interactions of short-scale and long-scale processes). The results are analysed to increase process understanding of the behavior of the system but are also parameterised so that they can be incorporated into a numerical model that covers a wider area. Kamphuis (2000)[6] discusses the use of various types of modelling and the need to provide well-based quantified results in coastal engineering design. He advocates integration of prototype data, physical and numerical modelling as a further element to improve modelling and design. These elements can essentially complement each other – model simulations provide the continuum information to bridge the gaps in field data, etc.

A key element in integrated models is the Computational module (“information manager”) as shown in the following figure.


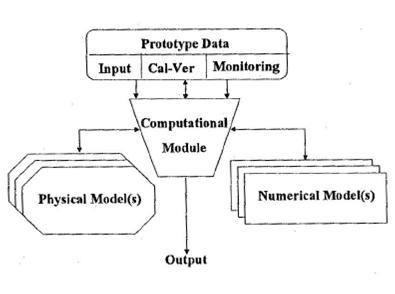
Fig 2.JPG
Figure 2: Model integration leading to an integrated model [4]


The integration of numerical modelling systems, field measurements, experimental laboratory research and theoretical analysis, combined through “calculation or integration modules” will lead to what is called “hybrid modelling” or “composite modelling”. For a problem with different spatial scales, modelling the far field by NM, and the near-field with PM, with proper exchange of information between the two, information exchange and results can be tied together computationally. An extensive range of topics have been identified as well as suited for a composite approach in hydraulic modeling [4]
A decision to apply CM is necessarily preceded by a problem analysis, in the form of the question and answers, in order to estimate a priori the potential benefits of using CM.
The state of the art of the tools for analysing the problem needs to be critically determined first. In different words and for obvious reasons somewhat aggregated we can rephrase that in the questions: Which individual approaches and models are available? Which level of sophistications is required / which model or set of models? Are their strengths and weakness such that they can be satisfactorily applied to analyse the problem given the type of answer required?
The answers to these questions will or should give the information whether it makes sense to use CM: Is one type of model not adequate for analysing and solving the problems? Do physical and numerical models complement each other for this problem? Can different scales be separated in time and / or in space? Can the interfacing of the models and the exchange of data be defined uniquely, in terms of quantified parameters? Can an estimate be given of the uncertainty of the transferred data, so the transfer and effect of uncertainties from model to model can be estimated? Oumeraci (1999)[2], Kamphuis (2000)[6] and Van Os et al. (2004)[7] point out the importance of this interfacing, which needs to be quantified, taking into account uncertainties involved. The above provides the material to formulate a hypothesis on what we expect to gain by CM for this problem, for example in terms of: increased cost effectiveness; improved accuracy; reducing uncertainties; tackling problems that could not reasonably be solved by a single model approach; etc. The outcome of this process is an argued decision on whether or not CM is needed, or whether it is beneficial for modeling the problem at hand.

The advantage of approaching this conscientiously lies in the fact that we systematically build up the various elements into, for instance, an exchangeable and easily accessible library of physical and numerical models and their descriptions or metadata. This will provide updates on their capabilities, usefulness, and track records which is part of Good Modelling Practice.

Phenomena and Concepts

The basic theory of the generation of storm surges and waves by wind is understood in principle [8] , although some details still need elucidation. For example, the wind stress is modelled empirically very successfully although the actual process of transfer of momentum and energy from the atmosphere to the sea via wind waves is very complex and not fully understood (Janssen 2004). There are also several interactions between the mean circulation and wind-waves (Peregrine and Jonsson 1983). The propagation of waves in shallow water is dependent on water depth and this means that the total water depth, which includes tide and surge, will affect wave propagation. In fact, the tidal propagation is also modified in the presence of a surge, leading to tide-surge interaction (Wolf 1981) [9]. Waves are modified by the presence of currents generated by tide and surge. They contribute to water level and mean circulation through wave setup and longshore currents, due to radiation stresses in shallow water (Longuet-Higgins and Stewart 1962).

Tides, caused by the gravitational effect of sun and moon, are periodic and very predictable. Surges, on the other hand, are quasi-periodic and caused by meteorological forcing. The most important mechanism for surge generation is wind-stress acting over shallow water. Surges at the coast are produced by Ekman dynamics, behaving as forced Kelvin waves [8]. The size of the surge is proportional to the wind-stress divided by the water depth. The wind-stress is usually taken to be proportional to the square of the wind-speed with a drag coefficient which increases with wind speed accounting for some effect of surface roughness due to waves [10].

Due to transient effects there is also an increase in surge height with wind duration. Surges are, therefore, largest where storms impact on large areas of shallow continental shelves. In deep water, surge elevations are approximately hydrostatic with a 1 hPa decrease in atmospheric pressure giving about 1 cm increase in surge elevation [11]. Surges in the Mediterranean as a whole are likely to be much lower due to the much deeper water. However, they are important in local areas of shallow water, e.g. the Northern Adriatic, where Venice is susceptible to flooding. Some modification is caused by seiching, when winds trigger oscillations at the natural periods of enclosed sea areas, e.g. in the Adriatic the wind tends to trigger the 22-h seiche [8]and its harmonics (11 and 7-h oscillations).
It has long been recognized that in shallow water areas with a large tidal range, the nonlinear effects of tide–surge interaction are important. The peak of the surge in the southern North Sea tends to ‘avoid’ predicted tidal high water, due to the speeding up of the tidal wave propagation in the presence of the deeper water caused by the surge level and other subtle changes are caused by bottom friction. Jones and Davies (1998)[12] and Horsburgh and Wilson (2007)[9], among others, have described work on the effects of tide–surge interaction.
Figure 3 illustrates the mechanism by which tide-surge interaction leads to a surge peak on the rising tide. The tidal phase is advanced due to the deeper water caused by the presence of a positive surge level. The difference between the phase-shifted (T0) and undisturbed tide (T) is added to the surge to give the net tidal residual (red line), which has a peak 3 h before predicted high water.


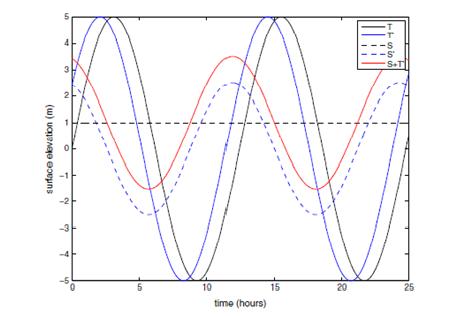
Fig 3.JPG
Figure 3: Illustration of tide-surge interaction. Undisturbed tide (predicted tide, T) is solid black line, phase advanced tide (T’) is solid blue line, meteorological surge (S) is dashed black line, tide-surge interaction (S’) is dashed blue line, net residual is solid red line ( Wolf, 2009)[13]


There are several mechanisms by which waves and the currents and water level associated with tide and surge interact, each component of the combined motion affecting the others [14].
These may be summarized as:

  1. the effects of water levels and currents on waves and
  2. the effect of waves on tides and surges.

First, the effect of water levels on nearshore wave transformation are considered. As waves enter shallow water, when the depth is less than half the wavelength, the processes of shoaling and refraction change the wavelength and phase speed but the wave period remains constant (in the absence of currents). As energy propagates at the group velocity, by energy conservation the wave height first decreases then increases (this is because of the group velocity property that it increases first with intermediate depth, only to decrease when the depth becomes shallower [15].
Finally, the energy dissipation processes of breaking and bottom friction start to limit the wave height. If the water depth is modified, by mean sea level changes or tide and/or surge, this will have corresponding effects on wave height. At the coast an increase in water depth will increase the wave height and also the distance to which waves can penetrate inland. Tide and surge currents can affect wave generation, propagation and dissipation. The effect on surface stress is to change the apparent wind and effective fetch. There may also be an enhancement of the wave friction in the bottom stress[16] although Soulsby and Clarke (2005)[17] state this is negligible. Current gradients in the horizontal also cause wave refraction and currents produce a Doppler shift of frequency.

References

  1. ↑ Sánchez-Arcilla, A. and Lemos, C.M. (1990). “Surf-zone Hydrodynamics”. Centro Internacional de Métodos Numéricos de Ingeniería, 310 p.
  2. ↑ 2.0 2.1 2.2 Oumeraci, H. (1999). Strengths and Limitations of Physical Modelling in Coastal Engineering - Synergy Effects with Numerical Modelling and Field Measurements. Proc. of the Hydralab -Workshop on Experimental Research and Synergy Effects with Mathematical Models, Eds.: K.-U. Evers, J. Grune, A. van Os, Coastal Research Centre, Hannover
  3. ↑ Chau, KW (2010) Modelling for coastal hydraulics and engineering, Taylor and Francis Ltd., 231 pp.
  4. ↑ 4.0 4.1 4.2 Gerritsen, H., Sutherland, J., Deigaard, R., Sumer, B.M., Fortes, J, Sierra, J-P and Prepernau, U, (2009). Guidelines for Composite Modelling of the Interactions Between Beaches and Structures. Final Report, September, 66 pages, (HYDRALAB-III Deliverable JRA1.4).
  5. ↑ Barthel, V and E.R. Funke (1989). Hybrid modelling as applied to hydrodynamic research and testing. In: Recent Advances in Hydraulic Physical Modelling, R. Martins (Ed), NATO ASI Series E: Applied Sciences – vol. 165, Kluwer Academic Publishers.
  6. ↑ 6.0 6.1 Kamphuis, J.W. (2000). Designing with models. Proceedings of 27th International Conference on Coastal Engineering. Edge, B.L. (Ed) ASCE. pp 19 – 32.
  7. ↑ Van Os, A.G., Soulsby, R.S. and J. Kirkegaard (2004). The future role of experimental methods in European hydraulic research: towards a balanced methodology. Journal of Hydraulic Research, Vol. 42, No. 4, pp. 341-356.
  8. ↑ 8.0 8.1 8.2 Gill AE (1982) Atmosphere-ocean dynamics. Academic Press, London, 662 pp. Goring, D. G. (1978) Tsunamis - the propagation of long waves onto a shelf, Ph.D. dissertation, California Institute of Technology, Pasadena, CA.
  9. ↑ 9.0 9.1 Horsburgh KJ, Wilson C (2007) Tide–surge interaction and its role in the distribution of surge residuals inthe North Sea. J Geophys Res 112:C08003.
  10. ↑ Brown J, Wolf J (2009) Coupled wave and surge modelling for the eastern Irish Sea and implications for model wind-stress. Continental Shelf Research, 29, 1329-1342.
  11. ↑ Flather RA (2000) Existing operational oceanography. Coast Eng 41(1–3):13–40.
  12. ↑ Jones JE, Davies AM (1998) Storm surge computations for the Irish Sea using a three-dimensional numerical model with wave–current interaction. Cont Shelf Res 18:201–251.
  13. ↑ Wolf, J., 2009. Coastal Flooding – Impacts of coupled wave-surge-tide models. Natural Hazards, 9 (2), 241-260.
  14. ↑ Wolf J, Hubbert KP, Flather RA (1988) A feasibility study for the development of a joint surge and wave model. P.O.L. report, no 1, 109 pp.
  15. ↑ Wiegel RL (1964) Oceanographical engineering. Prentice Hall, Englewood Cliffs, New Jersey Williams JA.
  16. ↑ Grant WD, Madsen OS (1979) Combined wave and current interaction with a rough bottom. J Geophys Res 84(C4):1797–1808.
  17. ↑ Soulsby RL, Clarke S (2005) Bed shear-stresses under combined waves and currents on smooth and rough beds. Hydraulics research report TR 137.


The main author of this article is Prinos, Panayotis
Please note that others may also have edited the contents of this article.
Citation: Prinos, Panayotis (2012): Modelling coastal hydrodynamics. Available from http://www.coastalwiki.org/wiki/Modelling_coastal_hydrodynamics [accessed on 22-11-2024]
Retrieved from "https://www.coastalwiki.org/w/index.php?title=Modelling_coastal_hydrodynamics&oldid=53390"