Overtopping resistant dikes

Introduction

In 1953 the Netherlands experienced a major flooding. Studies determined that a lot of the breaches of the dikes were caused by overtopping (and even overflowing) of the dikes. The failure mostly started on the landward part of the structures. All dikes back then were constructed with a relative low crest and a steep landward slope. Since then all major water defences were raised and the landward slopes were made more gentle. The heightening of the dikes was done in such a manner that statistically only once in 10.000 years (in the western part of the Netherlands) 0.1 l/s per m of overtopping would occur. In the 1990ties by law it was decided that all major water defences should be assessed for safety. In these safety assessments it was found that al lot of dikes again should be raised in order to comply with the safety standards. This raised the question if the method to determine the rate of wave overtopping was correct or not. Also the question was put if the safety standard of 0.1 l/s per m once in 10.000 years was adequate. It turned out that that flooding the mechanisms not enough understood and therefore the safety standard was wrongfully determined on basis of testing with overflow instead of overtopping. Additionally, failure mechanisms were not adequate described. This lead to a Dutch national research program on loads on and strength of flood defences. To assess the erosion strength of grass covers on inner slopes and transition zones between slope to horizontal flats, destructive tests using a Wave Overtopping Simulator were performed at several dikes in the Netherlands.

A Wave Overtopping Simulator performs destructive tests on inner slopes of real dikes in order to establish the erosion resistance against overtopping waves from severe storms. The most relevant hydraulic processes to be considered at wave-structure interaction encompass wave reflection, wave dissipation, wave transmission resulting from wave overtopping and wave penetration through the porous structures, wave diffraction, run-up and wave breaking. Focusing on overtopping, additional processes such as trapped air on broken waves and turbulence, induced by local effects at the armour stones and breakwater cover layers, play an important role in order to determine wave induced dynamics. Formulations derived from these experimentations, are, in most of the cases, semiempirical in nature with their form based on physical considerations but empirical constants determined by fitting to experimental data. The role of scaling factors for dissipation mechanisms due to wave breaking, turbulence and generation of eddies in the fluid region as well as turbulence and friction within the porous material, is also not well established in the physical test. Besides the problem of the scaling technique, other features related with the duration of the experiment programs, wave flume dimensions or economical cost have to be considered. Due to poor repeatability, a large number of experiments have to be carried out in order to define confidence intervals. Moreover, experimental investigation on large-scale models is expensive and measurements within breaking waves can be very complex, due to the aerated and transient nature of the water surface. As a consequence, formulations extracted from the experimental tests present several restrictions. They can only be applied to a structure with a geometry similar or almost identical to the one tested and under identical wave characteristics. An analytical approach is not possible because of the complexity of the problem. A great effort has therefore been made over the last decades in the numerical modelling of wave interaction with coastal structures to overcome these limitations. Nonlinear Shallow Water (NSW), Boussinesq-type and Navier-Stokes equations models have traditionally been used. SPH models have also appeared in the last years as an alternative. However, they are in an early stage to be used as predictive tool.

Definition, design and function

Dikes and levees are applied everywhere there is a hinterland which needs protection against flooding. These protection measures prevent an area from flooding thus enabling economic and sociologic activities also at high water levels. The dikes are designed in such a way that they are geotechnical stable under normal and extreme conditions. Dutch dikes are designed permitting no overtopping. Of course no overtopping cannot be guaranteed. The structures which are described here are mainly grass covered inner or landward slopes of these dikes and levees such as the ones found in the Netherlands. They are mostly made with a sand core covered by a clay layer on the slopes and the crest.

Figure 1: Cross section of a Dutch dike

The typical geometry of dikes and levees is an outer or seaward slope then a crest and then a landward slope (right-hand side of Figure 1). The function of the landward slopes is stability of the dike structure and for guidance of overtopping waves or water flowing over the crest to the inlands. The landward slopes must be able to resist loads induced by design conditions. The slope angles as well as the width of the crest vary. In the Dutch case, sea dikes have a typical landward slope 1v:3h. River dikes are mostly steeper, up to 1v:2h. The height of the dikes also varies a lot. This depends on the local hydraulic conditions and on the norm frequency of water level for which the dike is designed. This varies from 1/10,000 per year for sea defences in the western part of the Netherlands to 1:1,250 years for dikes along rivers.

Dikes and levees protect up to a certain level. Absolute safety is impossible. The level to which a dike or a levee protects from flooding depends on the hydraulic regime, the physics of the structure (geometric and geotechnical) and the intended risk reduction or allowable risk to which it is designed. This implies that an economic optimum or in most cases the availability of funds defines the achievable level of risk reduction. Almost two third of the the Netherlands lays below sealevel and therefore has to be protected by dikes or other flood protection structures (including dunes). The dikes in the Netherlands are currently designed based on exceedance of a certain water level that is extrapolated from a long time series (over 200 years) and scientific hind casting. From these water levels, corresponding wave action is calculated. The combination of water level and hydraulic conditions determines the design conditions. Back in 1956, the first Delta Committee already did some early calculations and concluded that the level of protection of the western part of the Netherlands should be higher than in other parts (highest economic value). They found that this part should have a protection level (based on exceedance of water level) of once in a hundred thousand years. They knew dikes to have a large residual strength in the designs. They assumed this to be a factor 10 resulting in lowering the norm to once in ten thousand years. In 1996 the safety levels in the Netherlands were registered in the Water Defence Act. In 2009 this Act was replaced by the Water Act. In the Act of 1996 it was stated that the basis for the safety standards should be altered from exceedance of a certain water level to a risk based approach. This is now developing within the Dutch Floris project.

Experimental experience with function and performance

Onset

The landward slope of dikes proved a weak spot during the flooding of 1953 in the Netherlands (over 1,800 people drowned). Back then the dikes were much lower than today. This event led to the Delta Plan recommended heightening the dikes and to milden the landward slopes to 1:3 or even milder to reduce erosive impact of overtopping waves. Before 1953 the angels of the landward slopes were very steep 1:2 or even steeper. Another example is the impact of hurricane Katrina on New Orleans where a lot of landward slopes failed before the water level reached the crest of the levees. Water coming over the dikes or levees does not necessarily mean danger. If the area can cope with a certain amount of water without causing any or just minor socio-economic damage it may be allowable. To optimize costs and competition for space, the dimensions needed for flood protection is preferably limited. Allowing some water passing the crest of the dike by overtopping waves means the need to heighten (and widen) the dikes decreases. If the dikes are strong enough and the passing amount of water can be handled, the design level of the structure can be lowered. However the effect of overtopping water passing the crest of dikes is not known.

From 2006 and onward, Wave Overtopping Simulators were developed at 19 sections of dikes at 6 different locations in the Netherlands. Destructive tests have shown the behaviour of various inner slopes of dikes, embankments or levees under simulated of wave overtopping, up to a mean overtopping discharge of 125 l/s per m. The following will give a mid-term review, based on four years of destructive testing. Until 2009 overtopping tests with the overtopping simulator have been performed on real dutch dikes, with hydraulic loads consistent with more or less general extreme sea conditions along the Dutch coast (H_s = 2 m). The tests performed in 2010 were located along a river dike but the hydraulic loads induced were from a sea dike (H_s = 1-3 m). The main reason for the 2010 allocation was the fact that this sand dike had a very high sand content (85 and 95%) compared to clay covered dikes more commonly found along the dutch sea coast. The core of the dikes is usually sand although in some cases the core of the dike is bolder clay. The cover layer on the landward slopes of sand dikes is typically 0.6 m thick. The thickness of the cover on the sea side is mostly 1 m. In the test locations we indeed found clay covers on the landward slope mainly in the range of 0.6 m but also a location where the thickness of the clay cover only was 0.4 m was found. In the Netherlands dikes exist with a bolder clay core but these have not been tested yet.

Test results

Figure 3: Principle of Wave Overtopping Simulators

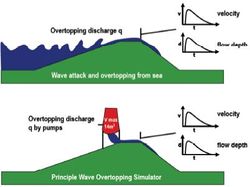
The process of wave overtopping on a dikes and levees is well known (Overtopping Manual, 2007). In contrast, the erosive impact of wave overtopping is not known well, mainly due to the fact that research on this topic cannot be performed on a small scale, as it is practically impossible to scale clay and grass down properly. Only some tests have been performed in large wave flumes, like the Delta flume in the Netherlands and the GWK in Germany, see Smith (1994) and Oumeraci et al. (2000). Therefore, the Wave Overtopping Simulator has been developed; see Van der Meer et al. (2006, 2007 and 2008) for more details. The Simulator consists of a high-level mobile box to store water (see Fig. 3). The maximum capacity is 5.5 m³ per m width (22 m³ for a 4 m wide Simulator). This box is continuously filled with a predefined discharge and emptied at specific times in such a way that it simulates the overtopping tongue of a wave at the crest and inner slope of a dike. The discharge of water is released in such a way that for each overtopping volume of water the flow velocity and thickness of the water tongue at the crest corresponds with the characteristics that can be expected.

Figure 4: Distribution of overtopping volumes of waves for sea dikes and various mean overtopping discharges, as simulated by the Wave Overtopping Simulator, based on Hs = 2 m and wave steepness 0.04 (peak period).

Field tests have been carried out at the end of the winter when grass roots are in their worst condition. The design and calibration of the Wave Overtopping Simulator has been described by Van der Meer (2007) and the test results of the first tested dike have been described by Akkerman et al. (2007a and 2007b). Part of the tests in 2008 have been described by Steendam et al. (2008). A summary report on all the testing in 2007 and 2008 has been described by Van der Meer (2008). Each test condition was given by a mean discharge and lasted for 6 hours. Test conditions increased from 0.1 l/s per m to 1; 5; 10; 30; 50 and 75 l/s per m. A full test on a dike section took about one week and often more than 14,000,000 litres of water flowed over the inner slope of 4 m width. Each test condition consisted of simulation of the required distribution of overtopping volumes (Overtopping Manual, 2007). Such a distribution depends on expected conditions at sea: a larger significant wave height (as at sea dikes) will show fewer overtopping waves, but the volume in the overtopping waves will be bigger than for a smaller wave height (as for example at river dikes). All tests until 2009 have assumed a significant wave height of 2 m with a wave steepness of 0.04 (using the peak period). In 2010 also tests have been performed with a significant wave height of 3 m and 1 m. Distributions of overtopping volumes for this condition and for various mean discharges are given in Figure 4.

Figure 4 clearly shows that for each mean discharge there are only a small number of waves that give large overtopping volumes. The general behaviour of wave overtopping can be described by a large number of fairly small overtopping waves and a few which are much bigger. These few but bigger waves often cause the damage to the inner slope. In the first years of testing it appeared to be very difficult to measure any hydraulic parameter on the inner slope, like flow velocity or flow depth. The velocities can approach 8 m/s and the water is very turbulent with a lot of air entrainment (estimated to be about 10%). The maximum flow depth is about 0.25 m. It is assumed that the front velocity is similar to the maximum depth averaged velocity and that flow velocity and flow depth have the same shape of record in time. Wave overtopping may lead to failure of the crest and inner slope of a dike. In principle there are two different failure mechanisms. Fast overtopping water may damage the surface of the crest and inner slope and, if initial damage or erosion has occurred, this may continue to the layer underneath the grass cover and may lead to an initial breach. This is actually the process which is simulated by the Wave Overtopping Simulator: erosion of the slope. A major failure mechanism on steep inner faces (typically 1:1.5 and 1:2) in the past was slip failure of the (rear) slope. Such slip failures may lead directly to a breach. For this reason most dike designs in the Netherlands in the past fifty years have used a 1:3 inner slope, where it is unlikely that slip failures will occur due to overtopping. This mechanism might however occur for inner slopes steeper than 1:3 and should then be taken into account in safety analysis. This failure mechanism is not simulated by the overtopping tests, as a slip failure needs more width to develop than the 4 m wide test section.

Figure 5: Example of damage by the wave overtopping simulations at Saint Philips

Inner slopes of a dike, covered with grass on clay, never failed by overtopping wave erosion for a mean overtopping discharge of 30 l/s per m or less. Only one section failed at 50 l/s per m; some although not all at 75 l/s per m. Large erosion resistance of the inner slope of a dike is determined by the combination of grass and clay. The grass cover seems stronger if it grows on sandy clay and may even resist up to 75 l/s per m. But if significant damage occurs, the clay layer is not very erosion resistant. Since grass roots can barely penetrate good quality clay, no strong grass cover could be found. Here grass may rip off for overtopping discharges around 30 l/s per m although the remaining good quality clay layer, still reinforced with some roots, has a large erosion resistance against overtopping waves. Therefore a good grass cover on a sandy clay and a worse grass cover on good clay show different failure mechanisms but similar strength against wave overtopping. Thus the grass sod and its way of maintenance may have less influence on the total strength than previously anticipated. Bad grass coverage (small open areas without grass) on sandy clay may show less resistance (Fig. 5). Transitions from slope to horizontal such as the transition from the inner slope to the toe of the dike are probably the most critical locations for initial and increasing damage. Damage here was initiated by a mean discharge of 10 l/s per m or more. As the damage occurred at the lowest part of the inner slope it will take time for damage to extend to the crest level and subsequently cause a dike breach. Transitions higher on the inner slope might be more critical. A hole in the layer of clay created at a large mean overtopping discharge of 50 l/s per m or more which reaches the under laying sand core, will give a very quick ongoing erosion. Although a test with a parking place of bricks showed that sand erosion at 10 l/s per m or more, goes fairly quickly (was even stopped at 30 l/s per m due to fast ongoing damage to the parking area) the dike itself was not in danger at all. Small obstacles like poles and fences did not show any erosion. Small holes from mice and moles did not initiate damage to the grass cover layer. An obstacle like a concrete staircase on the inner slope was totally destroyed at a stage with 75 l/s per m overtopping but the dike itself was not in danger.

Numerical Modelling efforts

Nonlinear Shallow Water (NSW) models

The use of NSW models to simulate surf zone hydrodynamics and wave structure interaction has been subjected to two approaches, wave averaged models and the more commonly used time domain models. However these fail to generate a valid wave theory for the wave breaking process by their basic assumptions i.e. the wave height is not small in comparison to water depth, and the change in depth is not small over a characteristic horizontal length for motion (Svendsen, 2005). This problem has been partially solved by assuming a hydrostatic pressure distribution, a depth-uniform velocity profile, negligible vertical accelerations, and simple parameterization of the turbulent terms in the equations of motion and the flow within porous media. All these assumptions allow the use of depth-integrated nonlinear shallow water equations models near coastal structures. Despite assumptions and limitations, models based on NSL equations are very efficient and cheap. Simulations containing many waves can be calculated rapidly being a valid alternative under certain conditions. The capability of the one-dimensional depth-averaged nonlinear shallow water equations model with bore-like dissipation and quadratic bottom friction model for the study of wave overtopping was first tested by Kobayashi and Raichle (1994). The model, called RBREAK, was essentially based on the previous work of Kobayashi and Wurjanto (1989), in which a system of conservation equations of mass, momentum and energy was derived from the two dimensional Reynolds equations. Wave breaking was assumed to occur numerically in the flow field triggered artificially. The model under predicted overtopping thickness by a factor of 5. However, the mean overtopping rate was at large under predicted by the model. Kobayashi and Wurjanto (1989) and subsequently Dodd (1998) validated their NLSW models against a data set of monochromatic wave overtopping of a sloping sea wall by Saville (1955). The seawall was situated on a shallow foreshore, which accommodated the conditions for wave breaking. Again, the average discharge was considerably under predicted by both models, particularly for tests of high wave steepness. The failure in reproducing the mean water level by the model was attributed to the inability of the NLSW model in describing the complex wave interactions in the surf zone, in which wave setup results. More recently Kobayashi et al. (2010), has improved the model introducing a probabilistic model to the NSW equations. Another example of a well known model based on the NSW equations is AMAZON presented by Hu et al. (2000). The AMAZON model solutions were compared with analytical solutions and laboratory data for wave overtopping at sloping and vertical seawalls and good agreement was found. The model is still under development and requires more verification tests for irregular waves before its application as a generic design tool. Modeling of wave transformation over reefs involves energetic wave breaking and transition between sub and supercritical flows. The conservative form of the nonlinear shallow-water equations and the associated numerical schemes are uniquely suitable to describe these processes (e.g., Toro, 2001; LeVeque, 2002). Godunov-type schemes based on a Riemann solver have remarkable shock-capturing capabilities to describe breaking waves as bores and conserve flow volume and momentum across discontinuities. Researchers have applied shock-capturing finite volume schemes in coastal and riverine flood hazard modeling (e.g., Dodd, 1998; Pan et al., 2007; Begnudelli et al., 2008). Although these applications are relevant in some aspects to surf-zone processes, the lack of dispersion in the nonlinear shallow-water equations hampers their application to near shore wave modeling.

Smoothed Particle Hydrodynamics (SPH) models

SPH (Smoothed Particle Hydrodynamics) models have recently been applied to coastal engineering. This approach solves the flow from the Lagrangian point of view, calculating the kinematics of each particle and its interaction with neighbour particles. The Lagrangian nature of SPH makes it well suited to simulate free surface flows with rapid changes of the flow field. However, SPH models are very expensive from the computational point of view and they cannot be applied to solve the large domains requested by wave-structure interaction. They cannot be used to simulate many waves to provide a statistical representation of wave overtopping. A detailed explanation of the SPH theories and formulations can be found in Monaghan, (1992) although the method was first applied to coastal engineering by Dalrymple et al. (2001). Several works have been published in the last decade such as Gotoh et al. (2004), Shao et al. (2006) or Dalrymple et al. (2006) among others, showing an ongoing progress on the definition of the boundary conditions and the improvement of the numerical prediction. More recently, Shao (2010) has published the first work describing wave interaction with a porous coastal structure. Model comparisons have been proved to describe the wave induced hydrodynamics. However, due to the high computational cost, the model cannot be used as predictive tool for overtopping.

Navier-Stokes models

Having less simplifying assumptions, Navier-Stokes equations (NSE) are free of some of the limitations mentioned above, allowing the calculation of the velocity field in the whole computational domain for either rotational or irrotational flows. These models are able to calculate flows in complex geometries and provide very refined information on the velocity, pressure and turbulence field. Moreover, Multi-layered structures and wave flow within the porous media can be simulated. One of the first numerical models of wave interaction with a permeable breakwater based on the bidimensional NSE is the one developed by Van Gent et al. (1994). The model, named SKYLLA, was able to simulate wave motions inside and outside porous structures, including breaking conditions. For free surface updating, the SKYLLA model uses the Volume Of Fluid (VOF) method introduced by Hirt and Nichols (1981) which consists of tracking the density change within each computational cell instead of the free surface location. Other models based on Navier-Stokes equations using the VOF method have been presented more recently. Iwata et al. (1996) investigated experimentally and numerically the breaking limit, breaking and post-breaking wave deformation due to three different types of submerged structures(i.e. bottom-seated, non-bottom-seated fixed and tautly moored) using a VOF-type model. The numerical model cannot simulate the porous flow in rubble-type breakwaters. In order to improve the knowledge of the wave breaking mechanisms, Lin and Liu (1998) developed a 2DV RANS-type numerical model named COBRAS (Cornell BReaking Waves And Structures). The model was a modified version of RIPPLE with a nonlinear k-e model for the closure of Reynolds stresses and a new set of boundary conditions to generate waves and VOF to track the free surface movements. Propagation, shoaling and breaking of a wave train in the surf zone was investigated, focusing on the turbulence transport mechanisms. Liu et al. (1999) improved the capability of the model including wave interaction with porous structures by spatially averaged Navier-Stokes equations. The internal drag forces were modelled by the empirical linear and nonlinear frictional forms. The authors assumed that turbulence inside the porous media is negligible, which is the case when the permeability of the medium is very small, i.e. for fine sands, but not in the breakwaters armour layer under pre-breaking waves as experimentally checked by Losada (2001) and Sakakiyama and Liu (2001). The numerical model was calibrated by simple experiments of flow passing through a porous dam. Hsu et al. (2002) extended the previous work introducing the effects of the small-scale turbulence in the porous media by a volume-averaging process of the governing equations. In their model based on the Volume-Averaged/Reynolds Averaged Navier-Stokes (VARANS) equations, the volume-averaged Reynolds stresses term was modelled by adopting the nonlinear eddy viscosity assumption. The model equations for the volume-averaged turbulent kinetic energy and its dissipation rate were derived by taking the volume-average of the standard k-e equations. The performance of the numerical model was checked by comparing numerical solutions with the experimental data related to a composite breakwater reported by Sakakiyama and Liu (2001), although detailed comparisons for turbulent magnitudes were not performed. The model was validated only for regular waves and for a limited number of experiments. In the last years, a great effort has been made in improving numerical models to study wave-structure interaction problems, especially for wave overtopping. A two-dimensional Reynolds Averaged Navier-Stokes (RANS) models (Losada et al., 2008; Lara et al., 2008; Guanche et al., 2009), called IH-2VOF have revealed that structural functionality and stability can be studied with a high degree of accuracy, even in the presence of granular material layers. VARANS have been solved to characterize wave induced flow within the porous structures. VARANS models, in a two dimensional form proved to overcome the inherent limitations presented by Nonlinear Shallow Water (NSW) and Boussinesq equations models related mainly with wave dispersion and breaking, vertical flow characterization, non-hydrostatic pressure field and flow inside porous coastal structures. Several approaches based on the use of Eulerian three dimensional Navier-Stokes sets of equations can be found in the literature, for example Li et al. (2004), Liu et al., (2009), Wang et al., (2009) or Christensen (2009), among others. However, none of them solved porous media flow and coastal structures are considered as impermeable. Hur et al. (2003) and more recently Hur et al. (2008) presented wave interaction with permeable structures using a three dimensional approach. Porous flow equations used in the simulations follow a different approach than presented by the VARANS equations. Although resistance forces due to the presence of porous material flow are represented in the same form, by drag and inertia terms, Navier-Stokes (NS) equations are not volume averaged. Aerial and volume porosities are defined and applied to the different terms of the NS equations, as aperture coefficients. More recently, Lara et al. (2010) has presented a new set of volume averaged set of equations for porous media flow. A k-e model was also integrated in the model. Validations were shown, obtaining a high degree of accuracy in the numerical predictions.

See also

Theseus Official Deliverable 2.1 - Integrated inventory of data and prototype experience on coastal defences and technologies

References

The main author of this article is De Rijcke, Maarten Please note that others may also have edited the contents of this article. Citation: De Rijcke, Maarten (2011): Overtopping resistant dikes. Available from http://www.coastalwiki.org/wiki/Overtopping_resistant_dikes [accessed on 21-11-2024] For other articles by this author see Category:Articles by De Rijcke, Maarten For an overview of contributions by this author see Special:Contributions/MaartenDeRijcke