Difference between revisions of "Salinity sensors"
Dronkers J (talk | contribs) |
Dronkers J (talk | contribs) |
||
| Line 15: | Line 15: | ||
</div> | </div> | ||
| − | "Salinity is the total amount of solid materials, in grams, dissolved in one kilogram of sea water when all the carbonate has been converted to oxide, the bromine and iodine replaced by chlorine and all organic matter completely oxidized | + | '''Definition of Salinity, [[International Council for the Exploration of the Sea (ICES)| ICES]], 1902''' |
| + | |||
| + | "Salinity is the total amount of solid materials, in grams, dissolved in one kilogram of sea water when all the carbonate has been converted to oxide, the bromine and iodine replaced by chlorine and all organic matter completely oxidized <ref>KNUDSEN, M. 1901. Hydrographical tables. G.E.C. Gad, Copenhagen, 63p </ref>. | ||
Although this definition is correct and served oceanographers for the next 65 years, the methodology is impractical and difficult to carryout with precision. Knowing that the seawater composition was constant and chlorine could be accurately measured by silver volumetric titration, the commission defined "chlorinity" as a measure of salinity. After analyzing several samples from nine locations, Knudsen and his colleagues developed an equation to calculate salinity based on chlorine content: | Although this definition is correct and served oceanographers for the next 65 years, the methodology is impractical and difficult to carryout with precision. Knowing that the seawater composition was constant and chlorine could be accurately measured by silver volumetric titration, the commission defined "chlorinity" as a measure of salinity. After analyzing several samples from nine locations, Knudsen and his colleagues developed an equation to calculate salinity based on chlorine content: | ||
<br> | <br> | ||
| − | <math>S=1.805\ Cl +0.03\quad </math> | + | <math>S=1.805\ Cl +0.03 \quad </math>‰ |
| − | |||
where chlorinity <math>Cl</math> is defined as the mass of silver required to precipitate completely the halogens in 0.3285234kg of the sea-water sample: | where chlorinity <math>Cl</math> is defined as the mass of silver required to precipitate completely the halogens in 0.3285234kg of the sea-water sample: | ||
| − | |||
| − | <math>Cl = 328.5234\ Ag \quad</math> | + | <math>Cl = 328.5234\ Ag \quad</math>‰ |
| − | + | ||
===JPOTS - 1966=== | ===JPOTS - 1966=== | ||
| − | As seen from the formula above, this method has its limitations and is not entirely correct: when chlorinity is 0, salinity is 0.03. Furthermore, Carritt and Carpenter (1959) have estimated that the uncertainty of a computed value of salinity from a measured value of chlorinity using this relation can be as much as 0.04‰. This is due to variations in the chemical composition in some seawater samples (Baltic) and the fact that only 9 different locations were sampled to define chlorinity. | + | As seen from the formula above, this method has its limitations and is not entirely correct: when chlorinity is 0, salinity is 0.03. Furthermore, Carritt and Carpenter (1959<ref>Carritt, D. E. and Carpenter, J . H. 1959.. The composition of sea water and the salinity-chlorinity-density problems. In Physical and Chemical Properties of Sea Water, pp. 67-86. Nat. Acad. Sci. Pub. 600; 202 pp.</ref>) have estimated that the uncertainty of a computed value of salinity from a measured value of chlorinity using this relation can be as much as 0.04‰. This is due to variations in the chemical composition in some seawater samples (Baltic) and the fact that only 9 different locations were sampled to define chlorinity. |
In the beginning of the 60's, with the development of conductivity bridges, it became possible to measure salinity with great precision (± 0.003‰) . Bridges gave conductivity ratios between the sample and standard seawater used to calibrate the bridges. However the standard seawater had been developed for chlorinity measurements and not for conductivity, so a new conductivity standard was commissioned to the Joint Panel for Oceanographic Tables and Standards (JPOTS) and based on new measurements of salinity, temperature and conductivity from samples around the world, the standing formula of chlorinity was revised to: | In the beginning of the 60's, with the development of conductivity bridges, it became possible to measure salinity with great precision (± 0.003‰) . Bridges gave conductivity ratios between the sample and standard seawater used to calibrate the bridges. However the standard seawater had been developed for chlorinity measurements and not for conductivity, so a new conductivity standard was commissioned to the Joint Panel for Oceanographic Tables and Standards (JPOTS) and based on new measurements of salinity, temperature and conductivity from samples around the world, the standing formula of chlorinity was revised to: | ||
| − | + | ||
| − | <math>S = 1.80655\ Cl</math> | + | <math>S = 1.80655\ Cl \quad</math>‰ |
| − | + | ||
===Practical Salinity Scale-1978 / EOS-80=== | ===Practical Salinity Scale-1978 / EOS-80=== | ||
The relation between salinity and conductivity ratio was based on precise determinations of chlorinity and [[Conductivity ratio|''R<sub>15</sub>'']] on 135 natural seawater samples, all collected within 100 m of the surface, and including samples from all oceans and the Baltic, Black, Mediterranean, and Red Seas. After chlorinity was converted to salinity, using the formula shown previously, the following polynomial was computed by least squares: | The relation between salinity and conductivity ratio was based on precise determinations of chlorinity and [[Conductivity ratio|''R<sub>15</sub>'']] on 135 natural seawater samples, all collected within 100 m of the surface, and including samples from all oceans and the Baltic, Black, Mediterranean, and Red Seas. After chlorinity was converted to salinity, using the formula shown previously, the following polynomial was computed by least squares: | ||
| − | |||
<math> S = 0.0080-0.1692{R_T}^{\frac {1} {2}} + 25.3853 {R_T} + 14.0941 {R_T}^{\frac {3}{2}}- 7.0261{R_T} ^2 + 2.7081{R_T}^{\frac {5}{2}}+ \Delta S</math> | <math> S = 0.0080-0.1692{R_T}^{\frac {1} {2}} + 25.3853 {R_T} + 14.0941 {R_T}^{\frac {3}{2}}- 7.0261{R_T} ^2 + 2.7081{R_T}^{\frac {5}{2}}+ \Delta S</math> | ||
| − | + | <math> R_T = \large\frac {C (S, T, 0)} {C (KCl, T, 0)}</math> | |
| − | |||
| − | <math> R_T = \frac {C (S, T, 0)} {C (KCl, T, 0) | ||
| − | |||
| − | |||
| − | |||
| + | <math>\Delta S = \Large\frac {(T - 15)} {(1 + 0.0162(T - 15))}\normalsize + 0.005 - 0.0056 {R_T}^{\frac{1}{2}} - 0.0066 {R_T} -</math><math>- 0.0375 {R_T}^{\frac{3} {2}} + 0.636 {R_T}^{2} - 0.0144 {R_T}^{\frac{5} {2}}</math> | ||
| + | for <math> 2 \, \le S \le \, 42 </math>, | ||
| − | |||
| − | |||
| − | |||
| − | |||
where C (S, T, 0) is the conductivity of the sea-water sample at temperature T and standard atmospheric pressure, and C (KCl, T, 0) is the conductivity of the standard potassium chloride (KCl) solution at temperature T and standard atmospheric pressure. The standard KCl solution contains a mass of 32.4356 grams of KCl in a mass of 1 kg of solution, and the conductivity of this solution at 15°C and 1 atmosphere is exactly 35. | where C (S, T, 0) is the conductivity of the sea-water sample at temperature T and standard atmospheric pressure, and C (KCl, T, 0) is the conductivity of the standard potassium chloride (KCl) solution at temperature T and standard atmospheric pressure. The standard KCl solution contains a mass of 32.4356 grams of KCl in a mass of 1 kg of solution, and the conductivity of this solution at 15°C and 1 atmosphere is exactly 35. | ||
| Line 61: | Line 53: | ||
===TEOS-10=== | ===TEOS-10=== | ||
| − | Quite recently adopted by UNESCO's IOC and still under scrutiny by both sensor manufacturers and oceanographers, the new thermodynamic equation of state was based on the fact that seawater composition changes with depth (see box bellow). The points that motivated an updated thermodynamic description of seawater are shown bellow as stated by Mcdougall | + | Quite recently adopted by UNESCO's IOC and still under scrutiny by both sensor manufacturers and oceanographers, the new thermodynamic equation of state was based on the fact that seawater composition changes with depth (see box bellow). The points that motivated an updated thermodynamic description of seawater are shown bellow as stated by Mcdougall et al., 2009<ref>McDougall, T.J., R. Feistel, F. J. Millero, D. R. Jackett, D. G. Wright, B. A. King, G. M. Marion, C. T. A. Chen and P. Spitzer, 2009: Calculation of the Thermophysical Properties of Seawater, Global Shipbased Repeat Hydrography Manual, IOCCP Report No. 14, ICPO Publication Series no. 134</ref> and Feistel et al., 2016<ref>Feistel, R., Wielgosz, R., Bell, S.A., Camoes, M.F., Cooper, J.R., Dexter, P., Dickson, A.G., Fisicaro, P., Harvey, A.H., Heinonen, M., Hellmuth, O., Kretzschmar, H-J., Lovell-Smith, J.W., McDougall, T.J., Pawlowicz, R., Ridout, P., Seitz, S., Spitzer, P., Stoica, D. and Wolf, H. 2016. Metrological challenges for measurements of key climatological observables: Oceanic salinity and pH, and atmospheric humidity. Part 1: Overview. Metrologia 53(1): R1–R11</ref>. |
| + | |||
{|style="margin: 1em 2em 1em 1em;border: 1px solid #00787A; float:right" cellspacing="1" cellpadding="5" width="460" | {|style="margin: 1em 2em 1em 1em;border: 1px solid #00787A; float:right" cellspacing="1" cellpadding="5" width="460" | ||
| | | | ||
| Line 74: | Line 67: | ||
*The impact on seawater density of the variation of the composition of seawater in the different ocean basins has become better understood. | *The impact on seawater density of the variation of the composition of seawater in the different ocean basins has become better understood. | ||
*The increasing emphasis on the ocean as being an integral part of the global heat engine points to the need for accurate expressions for the enthalpy and internal energy of seawater so that heat fluxes can be more accurately determined in the ocean (enthalpy and internal energy were not available from EOS-80). | *The increasing emphasis on the ocean as being an integral part of the global heat engine points to the need for accurate expressions for the enthalpy and internal energy of seawater so that heat fluxes can be more accurately determined in the ocean (enthalpy and internal energy were not available from EOS-80). | ||
| − | *The temperature scale has been revised from ITS-68 to ITS-90 and the atomic weights of the elements have been revised | + | *The temperature scale has been revised from ITS-68 to ITS-90 and the atomic weights of the elements have been revised. |
==Sensors== | ==Sensors== | ||
| Line 85: | Line 78: | ||
Conductivity, C, is found using the following formula: | Conductivity, C, is found using the following formula: | ||
[[Image: conductivity cell.JPG | 400px| thumb| right| A conductivity cell. Current flows through the seawater between platinum electrodes in a cylinder of borosilicate glass 191 mm long with an inside diameter between the electrodes of 4 mm. The electric field lines (solid lines) are confined to the interior of the cell in this design making the measured conductivity (and instrument calibration) independent of objects near the cell. ''From Sea-Bird Electronics'']] | [[Image: conductivity cell.JPG | 400px| thumb| right| A conductivity cell. Current flows through the seawater between platinum electrodes in a cylinder of borosilicate glass 191 mm long with an inside diameter between the electrodes of 4 mm. The electric field lines (solid lines) are confined to the interior of the cell in this design making the measured conductivity (and instrument calibration) independent of objects near the cell. ''From Sea-Bird Electronics'']] | ||
| − | + | ||
<math>C=G\cdot kc </math> | <math>C=G\cdot kc </math> | ||
| − | + | ||
where | where | ||
| − | + | ||
| − | <math>G</math> is the conductance, and kc is the cell constant. The cell constant is determined for a probe using the following formula: | + | <math>G</math> is the conductance, and <math>kc</math> is the cell constant. The cell constant is determined for a probe using the following formula: |
| − | + | ||
| − | <math>kc = \frac{d}{A}</math> | + | <math>kc = \Large\frac{d}{A}</math> |
| − | + | ||
where <math> d </math> is the distance between the two electrodes, and <math>A</math> is the area of the electrode surface. For example, the Conductivity Sensor has a cell constant, for instance: | where <math> d </math> is the distance between the two electrodes, and <math>A</math> is the area of the electrode surface. For example, the Conductivity Sensor has a cell constant, for instance: | ||
| − | + | ||
| − | <math>kc = \frac{d}{A} = \frac{1.0 cm}{0.1 cm^2} = 10 cm^{-1}</math> | + | <math>kc = \Large \frac{d}{A}\normalsize = \Large\frac{1.0 cm}{0.1 cm^2}\normalsize = 10 \, cm^{-1}</math> |
| − | + | ||
The conductivity value is found by multiplying conductance and the cell constant. | The conductivity value is found by multiplying conductance and the cell constant. | ||
A potential difference is applied to the two probe electrodes in the Salinity Sensor. The resulting current is proportional to the conductivity of the solution. This current is converted into a voltage. | A potential difference is applied to the two probe electrodes in the Salinity Sensor. The resulting current is proportional to the conductivity of the solution. This current is converted into a voltage. | ||
Revision as of 16:07, 20 August 2020
Contents
Salinity measurements and definitions throughout history
Since as far as Ancient Greece times, attempts have been made to try to measure the "saltiness" of seawater. However, methods' efficiency was very incipient and their sensitivity and repeatability was very limited. During the Modern History more precise methodologies were developed: weighing after evaporation (Boyle,1693; Birch, 1965), solvent extraction (Lavoisier, 1772) and precipitation (Bergman, 1784). In 1865, Forchhammer introduced the term salinity and dedicated himself to measure individual components of seasalt rather than the total salinity. He found that the ratio of major salts in samples of seawater from various locations was constant. This constant ratio is known as Forchhammer's Principle, or the Principle of Constant Proportions. Towards the end of the nineteenth century, William Dittmar, following the work of Forchhammer, tested several methods to analyse the salinity and the chemical composition of seawater. The Dittmar methods for chemical analysis of the seawater were extremely precise. Dittmar analysed the chlorine content in seawater using silver nitrate precipitation of the chloride, and compared it with synthetically prepared seawater samples to vouch for the method's accuracy. He later analysed 77 samples from around the world, taken during the Challenger Expedition and noticed the same constancy of composition observed by Forchhammer: "although the concentration of the waters is very different, the percentage composition of the dissolved material is almost the same in all cases". [1]
ICES - 1902
With more accurate techniques to measure salinity, there was a need to have the same definition of salinity and measuring methods across the scientific community. In 1889, Martin Knudsen was named by ICES to preside a commission to address the salinity issues.
WHAT IS PSU? by Frank J. Millero in Oceanography Magazine, 1993
After receiving the latest issue of Oceanography, I was irritated by the Sea-Bird advertisement on the inside cover. It shows a TS diagram that is labeled with the term PSU. Although I have been unsuccessful in getting the company to discontinue the use of this term, I thought I should write this letter to express my concerns about its use my oceanographers in published articles. The term apparently is used to denote the use of the Practical Salinity Scale and is an abbreviation for Practical Salinity Unit. As a member of the Joint Panel on Oceanographic Tables and Standards that was instrumental in the development of the international equation of the state of seawater and the practical salinity scale, I am amazed that the practice that seems to have been adopted by oceanographers in using PSU. The practical salinity scale was defined as conductivity ratio with no units. A seawater sample with a conductivity ratio of 1.0 at 15ºC with a KCl solution containing a mass of 32.4356 g in a total mass of 1 kg of solution has a salinity of 35.000 (no units or ‰ are needed). The salinity and temperature dependence of this ratio for seawater weight evaporated or diluted with water led to the full definition of the practical salinity scale. This definition was adopted by all the National and International Oceanographic Organizations. It also was published in all the journal publishing oceanographic studies. Somewhere along the line oceanographers started to use the term PSU (practical salinity unit) to indicate that the practical salinity scale was used to determine conductivity salinity. This apparently resulted from the previous use ‰ to represent parts per thousand, which some oceanographers felt was a unit. The bottom line is that salinity has always been a ratio and does not have physical units. The use of the term PSU should not be permitted in the field and certainly not used in published papers. Whenever the practical salinity scale is used to determine salinity this should be stated somewhere in the paper. The use of the term PSS can be used to indicate that the Practical Salinity Scale is used. One certainly does not have to use to term PSU on all figures showing TS data. I should also point out that UNESCO (1985)[2] has published a SUN report that carefully outlines the use of units in the field of oceanography. This report was also adopted by all the International Oceanographic Societies but is not generally used by the oceanographers and the journals publishing oceanographic data. If the field of oceanography is to become a recognized science, it must adopt the units that are basic to the fields of chemistry and physics. It also should not adopt new units for variables that are unitless.
Definition of Salinity, ICES, 1902
"Salinity is the total amount of solid materials, in grams, dissolved in one kilogram of sea water when all the carbonate has been converted to oxide, the bromine and iodine replaced by chlorine and all organic matter completely oxidized [3].
Although this definition is correct and served oceanographers for the next 65 years, the methodology is impractical and difficult to carryout with precision. Knowing that the seawater composition was constant and chlorine could be accurately measured by silver volumetric titration, the commission defined "chlorinity" as a measure of salinity. After analyzing several samples from nine locations, Knudsen and his colleagues developed an equation to calculate salinity based on chlorine content:
[math]S=1.805\ Cl +0.03 \quad [/math]‰
where chlorinity [math]Cl[/math] is defined as the mass of silver required to precipitate completely the halogens in 0.3285234kg of the sea-water sample:
[math]Cl = 328.5234\ Ag \quad[/math]‰
JPOTS - 1966
As seen from the formula above, this method has its limitations and is not entirely correct: when chlorinity is 0, salinity is 0.03. Furthermore, Carritt and Carpenter (1959[4]) have estimated that the uncertainty of a computed value of salinity from a measured value of chlorinity using this relation can be as much as 0.04‰. This is due to variations in the chemical composition in some seawater samples (Baltic) and the fact that only 9 different locations were sampled to define chlorinity. In the beginning of the 60's, with the development of conductivity bridges, it became possible to measure salinity with great precision (± 0.003‰) . Bridges gave conductivity ratios between the sample and standard seawater used to calibrate the bridges. However the standard seawater had been developed for chlorinity measurements and not for conductivity, so a new conductivity standard was commissioned to the Joint Panel for Oceanographic Tables and Standards (JPOTS) and based on new measurements of salinity, temperature and conductivity from samples around the world, the standing formula of chlorinity was revised to:
[math]S = 1.80655\ Cl \quad[/math]‰
Practical Salinity Scale-1978 / EOS-80
The relation between salinity and conductivity ratio was based on precise determinations of chlorinity and R15 on 135 natural seawater samples, all collected within 100 m of the surface, and including samples from all oceans and the Baltic, Black, Mediterranean, and Red Seas. After chlorinity was converted to salinity, using the formula shown previously, the following polynomial was computed by least squares:
[math] S = 0.0080-0.1692{R_T}^{\frac {1} {2}} + 25.3853 {R_T} + 14.0941 {R_T}^{\frac {3}{2}}- 7.0261{R_T} ^2 + 2.7081{R_T}^{\frac {5}{2}}+ \Delta S[/math]
[math] R_T = \large\frac {C (S, T, 0)} {C (KCl, T, 0)}[/math]
[math]\Delta S = \Large\frac {(T - 15)} {(1 + 0.0162(T - 15))}\normalsize + 0.005 - 0.0056 {R_T}^{\frac{1}{2}} - 0.0066 {R_T} -[/math][math]- 0.0375 {R_T}^{\frac{3} {2}} + 0.636 {R_T}^{2} - 0.0144 {R_T}^{\frac{5} {2}}[/math]
for [math] 2 \, \le S \le \, 42 [/math],
where C (S, T, 0) is the conductivity of the sea-water sample at temperature T and standard atmospheric pressure, and C (KCl, T, 0) is the conductivity of the standard potassium chloride (KCl) solution at temperature T and standard atmospheric pressure. The standard KCl solution contains a mass of 32.4356 grams of KCl in a mass of 1 kg of solution, and the conductivity of this solution at 15°C and 1 atmosphere is exactly 35.
The present equation of seawater for seawater in use as the international standard for oceanography, is the 1980 International Equation of State of Seawater (EOS-80, released by the Joint Panel on Oceanographic Tables and Standards (JPOTS), and published by Millero et al. (1980). It is based on the temperature scale IPTS-68 and on the Practical Salinity Scale 1978, PSS-78 (Lewis and Perkin, 1981)
TEOS-10
Quite recently adopted by UNESCO's IOC and still under scrutiny by both sensor manufacturers and oceanographers, the new thermodynamic equation of state was based on the fact that seawater composition changes with depth (see box bellow). The points that motivated an updated thermodynamic description of seawater are shown bellow as stated by Mcdougall et al., 2009[5] and Feistel et al., 2016[6].
|
- Several of the polynomial expressions of the International Equation of State of Seawater (EOS-80) are not totally consistent with each other as they do not exactly obey the thermodynamic Maxwell cross-differentiation relations. The new approach eliminates this problem.
- Since the late 1970s a more accurate thermodynamic description of pure water has appeared (IAPWS-95). Also more and rather accurate measurements of the properties of seawater (such as for (i) heat capacity, (ii) sound speed and (iii) the temperature of maximum density) have been made and can be incorporated into a new thermodynamic description of seawater.
- The impact on seawater density of the variation of the composition of seawater in the different ocean basins has become better understood.
- The increasing emphasis on the ocean as being an integral part of the global heat engine points to the need for accurate expressions for the enthalpy and internal energy of seawater so that heat fluxes can be more accurately determined in the ocean (enthalpy and internal energy were not available from EOS-80).
- The temperature scale has been revised from ITS-68 to ITS-90 and the atomic weights of the elements have been revised.
Sensors
Platinum Electrode Conductivity Sensor
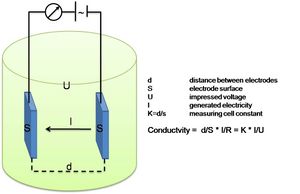
Salinity is a ratio and not a physical parameter that can be measured(under PSS-78, see box). Thus, “Salinity sensors” do not exist. What is commonly referred to as a salinity sensor is in fact a conductivity sensor.
This Conductivity Sensor measures the ability of a solution to conduct an electric current between two electrodes. In solution, the current flows by ion transport; therefore, an increasing concentration of ions in the solution will result in higher conductivity values. Conductance is defined as the reciprocal of resistance. When resistance is measured in ohms, conductance is measured using the SI unit, siemens (formerly known as a mho). Since the siemens is a very large unit, aqueous samples are commonly measured in microsiemens, or µS. Conductivity, C, is found using the following formula:

[math]C=G\cdot kc [/math]
where
[math]G[/math] is the conductance, and [math]kc[/math] is the cell constant. The cell constant is determined for a probe using the following formula:
[math]kc = \Large\frac{d}{A}[/math]
where [math] d [/math] is the distance between the two electrodes, and [math]A[/math] is the area of the electrode surface. For example, the Conductivity Sensor has a cell constant, for instance:
[math]kc = \Large \frac{d}{A}\normalsize = \Large\frac{1.0 cm}{0.1 cm^2}\normalsize = 10 \, cm^{-1}[/math]
The conductivity value is found by multiplying conductance and the cell constant. A potential difference is applied to the two probe electrodes in the Salinity Sensor. The resulting current is proportional to the conductivity of the solution. This current is converted into a voltage.
Electrodeless Conductivity Sensor (Inductive)
Electrodeless conductivity sensors use inductive coils. The inductive conductivity sensor consists of two coils which are incorporated next to one another in a polymer or ceramic body. These coils form current transformers. The sensor is designed so part of the liquid media forms a closed conductive current path passing through the coils. Current is applied to the primary coil (generating coil), which induces an alternating voltage in the liquid loop. In liquids which conduct electricity, this causes a current flow captured by the second coil (receiving coil), which is proportional to the conductivity of the sample solution.
Comparing the sensors
Electrode Sensors
- The main advantages of electrode sensors are:
- there is no proximity effect, the sensor can be mounted next to other sensors without interference
- easily calibrated in small baths
- The main disadvantages are:
- any changes in the cell constant will be reflected in the conductivity, and the cell cannot be cleaned in the field
- electrodes are subject to corrosion or damage (thought, most sensors used in oceanography are inside a cell that prevents this, as shown in the image above)
- electrodes inside a cell need seawater pumping which limits the measuring rate
Inductive Sensors
- The main advantages of inductive sensors are:
- robust construction
- they can be cleaned with soap or solvents and a brush.
- there are no electrodes, so there is no possibility of their damage.
- The main disadvantages are:
- a significant part of the measurement is external leading to major consequences result from this external field. The inductive sensors require a 3 inches radius from any other surface, from adjacent sensors. It is particularly difficult to address this problem in companion mounts such as ARGO floats or biological fouling.
- mounting and calibration of the sensor to companion packages (Argo floats, current meters, AUVs, etc.) must be undertaken to avoid intrusion into the external area. Because final package geometry influences the results, the calibration must be performed on the fully assembled package.
Calibration
- Zero Calibration Point: Simply perform this calibration point with the probe out of any liquid or solution (e.g., in the air). A very small voltage reading will be read. Call this value 0 ppt.
- Standard Solution Calibration Point: Place the Salinity Sensor into a standard solution (solution of known concentration). Wait for the displayed voltage to stabilize. Enter the value of the standard solution (e.g., 35 ppt).
See also
Historical overview of salinity measurements and definitions
Instruments and sensors to measure environmental parameters
References
- ↑ William J. Wallace (1974). The Development of the Chlorinity/Salinity Concept in Oceanography. Amsterdam: Elsevier. 239.
- ↑ UNESCO (1985) The international system of units (SI) in oceanography. UNESCO Technical Papers No.45, IAPSO Pub. Sci. No. 32, Paris, France.
- ↑ KNUDSEN, M. 1901. Hydrographical tables. G.E.C. Gad, Copenhagen, 63p
- ↑ Carritt, D. E. and Carpenter, J . H. 1959.. The composition of sea water and the salinity-chlorinity-density problems. In Physical and Chemical Properties of Sea Water, pp. 67-86. Nat. Acad. Sci. Pub. 600; 202 pp.
- ↑ McDougall, T.J., R. Feistel, F. J. Millero, D. R. Jackett, D. G. Wright, B. A. King, G. M. Marion, C. T. A. Chen and P. Spitzer, 2009: Calculation of the Thermophysical Properties of Seawater, Global Shipbased Repeat Hydrography Manual, IOCCP Report No. 14, ICPO Publication Series no. 134
- ↑ Feistel, R., Wielgosz, R., Bell, S.A., Camoes, M.F., Cooper, J.R., Dexter, P., Dickson, A.G., Fisicaro, P., Harvey, A.H., Heinonen, M., Hellmuth, O., Kretzschmar, H-J., Lovell-Smith, J.W., McDougall, T.J., Pawlowicz, R., Ridout, P., Seitz, S., Spitzer, P., Stoica, D. and Wolf, H. 2016. Metrological challenges for measurements of key climatological observables: Oceanic salinity and pH, and atmospheric humidity. Part 1: Overview. Metrologia 53(1): R1–R11
Please note that others may also have edited the contents of this article.
|