|
|
| (28 intermediate revisions by 4 users not shown) |
| Line 1: |
Line 1: |
| − | {{incomplete}}
| |
| − | {{revision}}
| |
| − | ''The authors below are planning to work on this article''
| |
| | | | |
| − | See also: [[Instruments and sensors to measure environmental parameters]]
| + | ==Practical Salinity== |
| | | | |
| | + | In the course of time, various methods have been developed to determine the salinity of seawater, see the article [[Salinity]]. The most practical method currently used is through electrical conductivity. Because this is an indirect method, an accurate relationship has been established between the conductivity <math>C</math> and the salinity <math>S</math> as a function of temperature <math>T</math> and pressure <math>p</math>. The salinity determined in this way is called the 'practical salinity'. The accuracy with which the conductivity of seawater can be measured is limited for reasons listed later in this article. Possible measurement errors can be eliminated, at least partly, by considering the relative conductivity <math>R</math>, the seawater conductivity <math>C(S,T)</math> relative to the conductivity <math>C(35,15)</math> of a standard saline solution at 15<sup>o</sup>C containing 32.4356 g KCl in a mass of 1 kg. The salinity of this standard solution is exactly 35. We omit pressure because it is only relevant for the deep ocean. The relationship between the salinity <math>S(T)</math> and the relative conductivity <math>R=R(S,T)</math> reads: |
| | | | |
| − | =='''Salinity measurements and definitions throughout history'''==
| + | <math>S(T) = S(15) + \Delta S(T) , \qquad R=\Large\frac{C(S,T)}{C(35,15)}\normalsize , \qquad (1)</math> |
| − | [[Image:DittmarTbl.PNG |thumb|400px|align:right| Constant composition of seawater (Dittmar, 1884)]] With more accurate techniques to measure salinity, there was a need to have the same definition of salinity and measuring methods across the scientific community. In 1889, Martin Knudsen was named by [[International Council for the Exploration of the Sea (ICES)| ICES]] to preside a commission to address the salinity issues.
| |
| − | '''Definition of Salinity, [[International Council for the Exploration of the Sea (ICES)| ICES]], 1902'''
| |
| − | Since as far as Ancient Greece times, attempts have been made to try to measure the "saltiness" of seawater. However, the low sensitivity and poor repeatability of the analytic methods at the time, meant that measurements were not sufficiently precise to be comparable. During the Modern History more precise methodologies were developed: weighing after evaporation (Boyle,1693; Birch, 1965), solvent extraction (Lavoisier, 1772) and precipitation (Bergman, 1784). In 1865, Forchhammer introduced the term salinity and dedicated himself to measure individual components of seasalt rather than the total salinity. He found that the ratio of major salts in samples of seawater from various locations was constant. This constant ratio is known as Forchhammer's Principle, or the Principle of Constant Proportions. Towards the end of the nineteenth century, William Dittmar, following the work of Forchhammer, tested several methods to analyse the salinity and the chemical composition of seawater. The Dittmar methods for chemical analysis of the seawater were extremely precise. Dittmar analysed the chlorine content in seawater using silver nitrate precipitation of the chloride, and compared it with synthetically prepared seawater samples to vouch for the method's accuracy. He later analysed 77 samples from around the world, taken during the Challenger Expedition and noticed the same constancy of composition observed by Forchhammer: "although the concentration of the waters is very different, the percentage composition of the dissolved material is ''almost'' the same in all cases". <ref> William J. Wallace (1974). The Development of the Chlorinity/Salinity Concept in Oceanography. Amsterdam: Elsevier. 239. </ref>
| |
| − | ===ICES - 1902===
| |
| − | <div style="border:1px solid #000000;float: right; background-color:#CEECF2;width: 250px;text-align: justify; padding:1em 1em 1em 1em; font-size:80%">
| |
| | | | |
| − | '''WHAT IS PSU? by Frank J. Millero ''in'' Oceanography Magazine, 1993'''
| + | <math>S(15)=0.008-0.1692\,R^{1/2}+25.3851\,R+14.0941\,R{3/2}-7.0261\,R^2+2.7081\,R^{5/2} , \qquad (2)</math> |
| | | | |
| − | After receiving the latest issue of ''Oceanography'', I was irritated by the Sea-Bird advertisement on the inside cover. It shows a TS diagram that is labeled with the term PSU. Although I have been unsuccessful in getting the company to discontinue the use of this term, I thought I should write this letter to express my concerns about its use my oceanographers in published articles. The term apparently is used to denote the use of the Practical Salinity Scale and is an abbreviation for Practical Salinity Unit.
| + | <math>\Delta S(T)= \Large\frac{T-15}{1+0.0162(T-15)}\normalsize (0.0005-0.0056\,R^{1/2} -0.0066\,R-0.0375\,R^{3/2}+0.0636\,R^2-0.0144\,R^{5/2}) , \qquad (3)</math> |
| − | As a member of the Joint Panel on Oceanographic Tables and Standards that was instrumental in the development of the international equation of the state of seawater and the practical salinity ''scale'', I am amazed that the practice that seems to have been adopted by oceanographers in using PSU. The practical salinity ''scale'' was defined as conductivity ratio with no units. A seawater sample with a conductivity ratio of 1.0 at 15ºC with a KCl solution containing a mass of 32.4356 g in a total mass of 1 kg of solution has a salinity of 35.000 (no units or ‰ are needed). The salinity and temperature dependence of this ratio for seawater weight evaporated or diluted with water led to the full definition of the practical salinity ''scale''. This definition was adopted by all the National and International Oceanographic Organizations. It also was published in all the journal publishing oceanographic studies.
| |
| − | Somewhere along the line oceanographers started to use the term PSU (practical salinity unit) to indicate that the practical salinity scale was used to determine conductivity salinity. This apparently resulted from the previous use ‰ to represent parts per thousand, which some oceanographers felt was a ''unit''. The bottom line is that salinity has always been a ratio and does not have physical units. The use of the term PSU should not be permitted in the field and certainly not used in published papers. Whenever the practical salinity scale is used to determine salinity this should be stated somewhere in the paper. The use of the term PSS can be used to indicate that the Practical Salinity ''Scale'' is used. One certainly does not have to use to term PSU on all figures showing TS data. I should also point out that UNESCO (1985)<ref>UNESCO (1985) The international system of units (SI) in oceanography. UNESCO Technical Papers No.45, IAPSO Pub. Sci. No. 32, Paris, France.</ref> has published a SUN report that carefully outlines the use of units in the field of oceanography. This report was also adopted by all the International Oceanographic Societies but is not generally used by the oceanographers and the journals publishing oceanographic data. If the field of oceanography is to become a recognized science, it must adopt the units that are basic to the fields of chemistry and physics. It also should not adopt new units for variables that are ''unitless''.
| |
| − | </div> | |
| | | | |
| − | "Salinity is the total amount of solid materials, in grams, dissolved in one kilogram of sea water when all the carbonate has been converted to oxide, the bromine and iodine replaced by chlorine and all organic matter completely oxidized <ref> http://www.aslo.org/lo/toc/vol_14/issue_3/0437.pdf </ref> <ref>KNUDSEN, M. 1901. Hydrographical tables. G.E.C. Gad, Copenhagen, 63p </ref>.
| + | for <math> 2 \, \le S \le \, 42 </math>. If R=1 we have S=35. |
| | | | |
| − | Although this definition is correct and served oceanographers for the next 65 years, the methodology is impractical and difficult to carryout with precision. Knowing that the seawater composition was constant and chlorine could be accurately measured by silver volumetric titration, the commission defined "chlorinity" as a measure of salinity. After analyzing several samples from nine locations, Knudsen and his colleagues developed an equation to calculate salinity based on chlorine content:
| |
| − | <br>
| |
| | | | |
| − | <math>S = 1.805\ Cl +0.03\quad </math><div style= "font-size:120%">‰</div>
| + | ==Sensors== |
| − | <br>
| |
| | | | |
| − | where chlorinity <math>Cl</math> is defined as the mass of silver required to precipitate completely the halogens in 0.3285234kg of the sea-water sample:
| + | ===Platinum Electrode Conductivity Sensor=== |
| − | <br>
| + | [[Image: electrode_conductivity.JPG | 300px| thumb |right| Electrode Conductivity principle]] |
| | | | |
| − | <math>Cl = 328.5234\ Ag \quad</math><div style= "font-size:120%">‰</div>
| + | As the practical salinity is not a physical parameter that can be measured directly, “Salinity Sensors” do not exist. What is commonly referred to as a salinity sensor is in fact a conductivity sensor. |
| − | <br>
| |
| | | | |
| − | ===JPOTS - 1966===
| + | This Conductivity Sensor measures the ability of a solution to conduct an electric current between two electrodes. In solution, the current flows by ion transport; therefore, an increasing concentration of ions in the solution will result in higher conductivity values. Conductance is defined as the reciprocal of resistance. When resistance is measured in ohms, conductance is measured using the SI unit, siemens (formerly known as a mho). Since the siemens is a very large unit, aqueous samples are commonly measured in microsiemens, or µS. |
| − | As seen from the formula above, this method has its limitations and is not entirely correct: when chlorinity is 0, salinity is 0.03. Furthermore, Carritt and Carpenter (1959) have estimated that the uncertainty of a computed value of salinity from a measured value of chlorinity using this relation can be as much as 0.04‰. This is due to variations in the chemical composition in some seawater samples (Baltic) and the fact that only 9 different locations were sampled to define chlorinity.
| + | [[Image: conductivity cell.JPG | 400px| thumb| right| A conductivity cell. Current flows through the seawater between platinum electrodes in a cylinder of borosilicate glass 191 mm long with an inside diameter between the electrodes of 4 mm. The electric field lines (solid lines) are confined to the interior of the cell in this design making the measured conductivity (and instrument calibration) independent of objects near the cell. ''From Sea-Bird Electronics'']] |
| − | In the beginning of the 60's, with the development of conductivity bridges, it became possible to measure salinity with great precision (± 0.003‰) . Bridges gave conductivity ratios between the sample and standard seawater used to calibrate the bridges. However the standard seawater had been developed for chlorinity measurements and not for conductivity, so a new conductivity standard was commissioned to the Joint Panel for Oceanographic Tables and Standards (JPOTS) and based on new measurements of salinity, temperature and conductivity from samples around the world, the standing formula of chlorinity was revised to:
| |
| − | <br>
| |
| − | <math>S = 1.80655\ Cl</math><div style="font-size:120%">‰</div>
| |
| − | <br>
| |
| | | | |
| − | ===Practical Salinity Scale-1978 / EOS-80===
| + | Conductivity, <math>C</math>, is found using the following formula: |
| | | | |
| − | The relation between salinity and conductivity ratio was based on precise determinations of chlorinity and [[Conductivity ratio|''R<sub>15</sub>'']] on 135 natural seawater samples, all collected within 100 m of the surface, and including samples from all oceans and the Baltic, Black, Mediterranean, and Red Seas. After chlorinity was converted to salinity, using the formula shown previously, the following polynomial was computed by least squares:
| + | <math>C=G\cdot kc , \qquad (4)</math> |
| − | <br> | |
| | | | |
| − | <math> S = 0.0080-0.1692{R_T}^{\frac {1} {2}} + 25.3853 {R_T} + 14.0941 {R_T}^{\frac {3}{2}}- 7.0261{R_T} ^2 + 2.7081{R_T}^{\frac {5}{2}}+ \Delta S</math> | + | where <math>G</math> is the conductance, and <math>kc</math> is the cell constant. The cell constant is determined for a probe using the following formula: |
| | | | |
| − | <br> | + | <math>kc = \Large\frac{d}{A}\normalsize , \qquad (5)</math> |
| | | | |
| − | <math> R_T = \frac {C (S, T, 0)} {C (KCl, T, 0)}</math>
| + | where <math> d </math> is the distance between the two electrodes, and <math>A</math> is the area of the electrode surface. The conductivity value is found by multiplying conductance and the cell constant. |
| − | | |
| − | <br>
| |
| − | <math>\Delta S = \frac {(T - 15)} {(1 + 0.0162(T - 15))}+ 0.005 - 0.0056 {R_T}^{\frac{1}{2}} - 0.0066 {R_T} -</math><math>- 0.0375 {R_T}^{\frac{3} {2}} + 0.636 {R_T}^{2} - 0.0144 {R_T}^{\frac{5} {2}}</math>
| |
| − | | |
| − | | |
| − | | |
| − | | |
| − | <br>
| |
| − | | |
| − | <math> For 2 \le S \le 42 </math>
| |
| − | <br>
| |
| − | | |
| − | | |
| − | | |
| − | | |
| − | | |
| − | where C (S, T, 0) is the conductivity of the sea-water sample at temperature T and standard atmospheric pressure, and C (KCl, T, 0) is the conductivity of the standard potassium chloride (KCl) solution at temperature T and standard atmospheric pressure. The standard KCl solution contains a mass of 32.4356 grams of KCl in a mass of 1 kg of solution, and the conductivity of this solution at 15°C and 1 atmosphere is exactly 35.
| |
| − | | |
| − | The present equation of seawater for seawater in use as the international standard for oceanography, is the 1980 International Equation of State of Seawater (EOS-80, released by the Joint Panel on Oceanographic Tables and Standards (JPOTS), and published by Millero et al. (1980). It is based on the temperature scale IPTS-68 and on the Practical Salinity Scale 1978, PSS-78 (Lewis and Perkin, 1981)
| |
| − | | |
| − | ===TEOS-10===
| |
| − | Quite recently adopted by UNESCO's IOC and still under scrutiny by both sensor manufacturers and oceanographers, the new thermodynamic equation of state was based on the fact that seawater composition changes with depth (see box bellow). The motivation for an updated thermodynamic description of seawater is shown bellow as stated by Mcdougall ''et. al'', 2009 <ref>McDougall, T.J., R. Feistel, F. J. Millero, D. R. Jackett, D. G. Wright, B. A. King, G. M. Marion, C. T. A. Chen and P. Spitzer, 2009: Calculation of the Thermophysical Properties of Seawater, Global Shipbased Repeat Hydrography Manual, IOCCP Report No. 14, ICPO Publication Series no. 134</ref>.
| |
| − | *Several of the polynomial expressions of the International Equation of State of Seawater (EOS-80) are not totally consistent with each other as they do not exactly obey the thermodynamic Maxwell cross-differentiation relations. The new approach eliminates this problem.
| |
| − | *Since the late 1970s a more accurate thermodynamic description of pure water has appeared (IAPWS-95). Also more and rather accurate measurements of the properties of seawater (such as for (i) heat capacity, (ii) sound speed and (iii) the temperature of maximum density) have been made and can be incorporated into a new thermodynamic description of seawater.
| |
| − | *The impact on seawater density of the variation of the composition of seawater in the different ocean basins has become better understood.
| |
| − | *The increasing emphasis on the ocean as being an integral part of the global heat engine points to the need for accurate expressions for the enthalpy and internal energy of seawater so that heat fluxes can be more accurately determined in the ocean (enthalpy and internal energy were not available from EOS-80).
| |
| − | *The temperature scale has been revised from ITS-68 to ITS-90 and the atomic weights of the elements have been revised (IUPAC, 2005).
| |
| − | | |
| − | {|style="margin: 1em 2em 1em 1em;border: 1px solid #00787A;" cellspacing="1" cellpadding="5" width="460" align="right"
| |
| − | |
| |
| − | {|border="0" cellspacing="0" cellpadding="0" width="100%"
| |
| − | |-valign="top"
| |
| − | |<div style="text-align: justify; font-size:95%;padding:1em 1em 1em 1em;"><span style="color:#00787A">'''In 1975, Brewer and Bradshaw suggested that changes in the composition of deep seawater can affect the conductivity-density relationship. This finding was followed by important papers discussing the limitations of the density-conductivity relationship that confirmed that samples from deep water had an elevated density due to the addition of Ca<sup>2+</sup> and HCO<sub>3</sub><sup>–</sup> from the dissolution of CaCO<sub>3</sub>(s), silicic acid (Si(OH)<sub>4</sub>) from the dissolution of SiO<sub>2</sub>(s), CO<sub>2</sub>, NO<sub>3</sub><sup>–</sup>, and PO<sub>4</sub><sup>3–</sup> from the oxidation of plant material (as predicted by Brewer and Bradshaw, 1975). '''</span></div>
| |
| − | |}
| |
| − | |}
| |
| − | | |
| − | ==Sensors==
| |
| − | ====Platinum Electrode Conductivity Sensor====
| |
| − | [[Image: electrode_conductivity.JPG | 300px| thumb |right| Electrode Conductivity principle]]
| |
| − | | |
| − | Salinity is a ratio and not a physical parameter that can be measured(under PSS-78, see box). Thus, “Salinity sensors” do not exist. What is commonly referred to as a salinity sensor is in fact a conductivity sensor.
| |
| − | | |
| − | This Conductivity Sensor measures the ability of a solution to conduct an electric current between two electrodes. In solution, the current flows by ion transport; therefore, an increasing concentration of ions in the solution will result in higher conductivity values. Conductance is defined as the reciprocal of resistance. When resistance is measured in ohms, conductance is measured using the SI unit, siemens (formerly known as a mho). Since the siemens is a very large unit, aqueous samples are commonly measured in microsiemens, or µS.
| |
| − | Conductivity, C, is found using the following formula:
| |
| − | [[Image: conductivity cell.JPG | 400px| thumb| right| A conductivity cell. Current flows through the seawater between platinum electrodes in a cylinder of borosilicate glass 191 mm long with an inside diameter between the electrodes of 4 mm. The electric field lines (solid lines) are confined to the interior of the cell in this design making the measured conductivity (and instrument calibration) independent of objects near the cell. ''From Sea-Bird Electronics'']]
| |
| − | <br>
| |
| − | <math>C=G\cdot kc </math>
| |
| − | <br>
| |
| − | where
| |
| − | <br>
| |
| − | <math>G</math> is the conductance, and kc is the cell constant. The cell constant is determined for a probe using the following formula:
| |
| − | <br>
| |
| − | <math>kc = \frac{d}{A}</math>
| |
| − | <br>
| |
| − | where <math> d </math> is the distance between the two electrodes, and <math>A</math> is the area of the electrode surface. For example, the Conductivity Sensor has a cell constant, for instance: | |
| − | <br>
| |
| − | <math>kc = \frac{d}{A} = \frac{1.0 cm}{0.1 cm^2} = 10 cm^{-1}</math>
| |
| − | <br>
| |
| − | The conductivity value is found by multiplying conductance and the cell constant. | |
| | A potential difference is applied to the two probe electrodes in the Salinity Sensor. The resulting current is proportional to the conductivity of the solution. This current is converted into a voltage. | | A potential difference is applied to the two probe electrodes in the Salinity Sensor. The resulting current is proportional to the conductivity of the solution. This current is converted into a voltage. |
| | | | |
| − | ====Electrodeless Conductivity Sensor (Inductive)====
| + | ===Electrodeless Conductivity Sensor (Inductive)=== |
| | [[Image: Induktive_Messung__eng.jpg|thumb|250px|right| Inductive conductivity sensor | | [[Image: Induktive_Messung__eng.jpg|thumb|250px|right| Inductive conductivity sensor |
| | principle]] | | principle]] |
| − | Electrodeless conductivity sensors use inductive coils. The inductive conductivity sensor consists of two coils which are incorporated next to one another in a polymer or ceramic body. These coils form a current transformer. The sensor is designed so part of the liquid media forms a closed conductive current path passing through the coils. Current is applied to the primary coil, which induces an alternating voltage in the liquid loop. In liquids which conduct electricity, this causes a current flow captured by the second coil, which is proportional to the conductivity of the sample solution. | + | Electrodeless conductivity sensors use inductive coils. The inductive conductivity sensor consists of two coils which are incorporated next to one another in a polymer or ceramic body. These coils form current transformers. The sensor is designed so part of the liquid media forms a closed conductive current path passing through the coils. Current is applied to the primary coil (generating coil), which induces an alternating voltage in the liquid loop. In liquids which conduct electricity, this causes a current flow captured by the second coil (receiving coil), which is proportional to the conductivity of the sample solution. |
| − | | |
| − | ===Comparing the sensors===
| |
| − | Inductive Sensors
| |
| − | | |
| − | *The main advantages of inductive sensors are robust construction, and that to preserve the geometry factor they can be cleaned with soap or solvents and a brush. There are no electrodes, so there is no possibility of their damage.
| |
| − | *The main disadvantages are that a significant part of the measurement is external leading to major consequences result from this external field. The inductive sensors require a 3'' radius
| |
| − | from any other surface, from adjacent sensors. It is particularly difficult to address this problem in companion mounts such as ARGO floats or biological fouling.
| |
| − | | |
| − | | |
| − | B. Mounting and calibration of the sensor to companion packages (Argo floats, current meters, AUVs, etc.) must be undertaken to avoid intrusion into the external area. Because final package geometry influences the results, the calibration must be performed on the fully assembled package.
| |
| − | | |
| − | | |
| − | A secondary disadvantage of the inductive cells is the requirement for oil-filling and pressure-balance ports. These are a source of unreliability and tend to drive up initial and long term costs. Potted cells that forego pressure balance are susceptible to plastic deformation and creep, leading to geometry changes and drift, especially in profiling applications.
| |
| − | | |
| − |
| |
| − | | |
| − | 2. C
| |
| − | | |
| − | The main advantages of Sea-Bird's electrode cells derive from their fully internal field. Because the field is internal, small amounts of antifoul material placed at the ends of the cell (but not in it) are demonstrably effective in preventing internal fouling and attendant drift.
| |
| − | | |
| − | Since there is no external field:
| |
| − | | |
| − | *There is no proximity effect. The SBE cell does not require mounting on the end of a fragile strut, and mechanical protection is easily arranged. Its rugged reliability has been proven in more than 6000 SBE cells that have been deployed long term and unattended -- large numbers on multiple deployments spanning many years.
| |
| − | | |
| − | *SBE conductivity sensors can be calibrated in small baths without concern for proximity effects. We routinely calibrate 10 sensors in one automatically controlled bath of less than 50 liters capacity, obtaining out of the box accuracy corresponding to better than 0.005 psu.
| |
| − | | |
| − | The primary disadvantage of the SBE sensor is its relatively poor flushing. While this is actually advantageous in that it enhances the antifoul capabilities of the cell, it is a drawback where very small spatial scales must be resolved. Generally, the SBE cell will give good results for measurements on second time scales for flow rates of 10 cm/second or more. Moored applications (with measurements typically on minute boundaries or greater) have exhibited scientifically satisfactory data even in low-flow environments.
| |
| − | | |
| − | A secondary disadvantage is that the SBE cell cannot be cleaned in the field. This is not generally important in autonomous or moored applications where no one will be there to do the cleaning!
| |
| − | | |
| − |
| |
| − | | |
| − | Common misconceptions about Sea-Bird conductivity cells
| |
| | | | |
| − | "The electrodes will corrode." The Sea-Bird cell's platinum electrodes are completely inert in seawater. They are AC coupled to preclude any galvanic effects. After thousands of deployments there is zero evidence of electrode corrosion or other electrode degradation in Sea-Bird cells.
| |
| | | | |
| − | "Two-terminal cells cannot give high accuracy." Published results prove otherwise. The Sea-Bird cell's large electrode area combined with the cell's high resistance override the limitations of two-terminal technique; for a negligible price in theoretical accuracy, the two-terminal configuration yields the enormous benefits of zero external field. Field deployments show the Sea-Bird cell to be at least as accurate, even for profiling, as the 4-terminal NBIS MKIII cell. Since Sea-Bird cells are protected from bio-fouling and are insensitive to proximity effects, they have proven much more accurate in moored and autonomous applications.
| + | ==Comparing the sensors== |
| | | | |
| − | "Sea-Bird's cell is fragile." The robustness of the borosilicate glass from which it is made is not much different from the ceramic used in competing designs. Because there is no external field, the Sea-Bird cell doesn't need strut mounting and it is practical to protect the cell with a mechanical guard. Thousands of successful deployments have been made with Sea-Bird cell-equipped instruments.
| + | ===Electrode Sensors=== |
| | + | *The main advantages of electrode sensors are: |
| | + | **there is no proximity effect, the sensor can be mounted next to other sensors without interference |
| | + | **easily calibrated in small baths |
| | + | *The main disadvantages are: |
| | + | **any changes in the cell constant will be reflected in the conductivity, and the cell cannot be cleaned in the field |
| | + | **electrodes are subject to corrosion or damage (however, most sensors used in oceanography are inside a cell that prevents this, as shown in the image above) |
| | + | **electrodes inside a cell need seawater pumping which limits the measuring rate |
| | | | |
| − | "You can't clean the Sea-Bird cell with a KimWipe or a bottle brush." True, but there will not be anyone riding an Argo float or an ocean mooring to clean an inductive cell, either.
| + | ===Inductive Sensors=== |
| | | | |
| − | "Electrodes foul. Inductive cells don't have electrodes to foul." The issue is not just whether electrodes foul, but whether the cell fouls. The fundamental unprotectability of inductive sensors results in fouling of the whole cell. This changes the cell constant and leads to unacceptable drift.
| + | *The main advantages of inductive sensors are: |
| | + | **robust construction |
| | + | **they can be cleaned with soap or solvents and a brush. |
| | + | **there are no electrodes, so there is no possibility of their damage. |
| | + | *The main disadvantages are: |
| | + | **a significant part of the measurement is external leading to major consequences resulting from this external field. The inductive sensors require a 3 inches radius from any other surface, from adjacent sensors. It is particularly difficult to address this problem in companion mounts such as ARGO floats or [[Biofouling | biological fouling]]. |
| | + | **mounting and calibration of the sensor to companion packages (Argo floats, current meters, AUVs, etc.) must be undertaken to avoid intrusion into the external area. Because final package geometry influences the results, the calibration must be performed on the fully assembled package. |
| | | | |
| − | "Sea-Bird conductivity sensors are expensive." We make only high-accuracy sensors and they are generally less expensive than competitive high accuracy types. High-accuracy Sea-Bird sensors are more expensive than the "Industrial-OEM" sensors made by FSI.
| + | ==Calibration== |
| | + | *Zero Calibration Point: Simply perform this calibration point with the probe out of any liquid or solution (e.g., in the air). A very small voltage reading will be read. Call this value 0 ppt. |
| | + | *Standard Solution Calibration Point: Place the Salinity Sensor into a standard solution (solution of known concentration). Wait for the displayed voltage to stabilize. Enter the value of the standard solution (e.g., 35). |
| | | | |
| | | | |
| − | ====Calibration==== | + | ==Related articles== |
| − | Zero Calibration Point: Simply perform this calibration point with the probe out of any liquid or
| + | :[[Salinity]] |
| − | solution (e.g., in the air). A very small voltage reading will be displayed on the LabNavigator. Call this value 0 ppt.
| + | :[[Seawater density]] |
| − | • Standard Solution Calibration Point: Place the Salinity Sensor into a standard solution (solution of known concentration). Be sure the entire elongated hole with the electrode surfaces is submerged in the solution. Wait for the displayed voltage to stabilize. Enter the value of the standard solution (e.g., 35 ppt). For further information on preparing standard solutions, see the next section.
| + | :[[Instruments and sensors to measure environmental parameters]] |
| | | | |
| − | ==See also==
| |
| − | Historical overview of salinity measurements and definitions
| |
| | | | |
| − | [[Category:Theme 9]]
| |
| − | [[Category:Techniques and methods in coastal management]]
| |
| − | [[Category:Hydrological processes and water]]
| |
| | | | |
| − | ==References== | + | {{author |
| | + | |AuthorID=26289 |
| | + | |AuthorFullName=Souza Dias, Francisco |
| | + | |AuthorName=Francisco Souza Dias}} |
| | | | |
| − | <references/>
| + | [[Category:Coastal and marine observation and monitoring]] |
| | + | [[Category:Observation of chemical parameters]] |
Practical Salinity
In the course of time, various methods have been developed to determine the salinity of seawater, see the article Salinity. The most practical method currently used is through electrical conductivity. Because this is an indirect method, an accurate relationship has been established between the conductivity [math]C[/math] and the salinity [math]S[/math] as a function of temperature [math]T[/math] and pressure [math]p[/math]. The salinity determined in this way is called the 'practical salinity'. The accuracy with which the conductivity of seawater can be measured is limited for reasons listed later in this article. Possible measurement errors can be eliminated, at least partly, by considering the relative conductivity [math]R[/math], the seawater conductivity [math]C(S,T)[/math] relative to the conductivity [math]C(35,15)[/math] of a standard saline solution at 15oC containing 32.4356 g KCl in a mass of 1 kg. The salinity of this standard solution is exactly 35. We omit pressure because it is only relevant for the deep ocean. The relationship between the salinity [math]S(T)[/math] and the relative conductivity [math]R=R(S,T)[/math] reads:
[math]S(T) = S(15) + \Delta S(T) , \qquad R=\Large\frac{C(S,T)}{C(35,15)}\normalsize , \qquad (1)[/math]
[math]S(15)=0.008-0.1692\,R^{1/2}+25.3851\,R+14.0941\,R{3/2}-7.0261\,R^2+2.7081\,R^{5/2} , \qquad (2)[/math]
[math]\Delta S(T)= \Large\frac{T-15}{1+0.0162(T-15)}\normalsize (0.0005-0.0056\,R^{1/2} -0.0066\,R-0.0375\,R^{3/2}+0.0636\,R^2-0.0144\,R^{5/2}) , \qquad (3)[/math]
for [math] 2 \, \le S \le \, 42 [/math]. If R=1 we have S=35.
Sensors
Platinum Electrode Conductivity Sensor
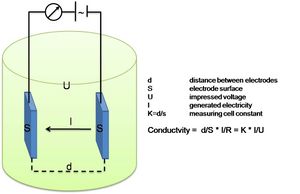
Electrode Conductivity principle
As the practical salinity is not a physical parameter that can be measured directly, “Salinity Sensors” do not exist. What is commonly referred to as a salinity sensor is in fact a conductivity sensor.
This Conductivity Sensor measures the ability of a solution to conduct an electric current between two electrodes. In solution, the current flows by ion transport; therefore, an increasing concentration of ions in the solution will result in higher conductivity values. Conductance is defined as the reciprocal of resistance. When resistance is measured in ohms, conductance is measured using the SI unit, siemens (formerly known as a mho). Since the siemens is a very large unit, aqueous samples are commonly measured in microsiemens, or µS.

A conductivity cell. Current flows through the seawater between platinum electrodes in a cylinder of borosilicate glass 191 mm long with an inside diameter between the electrodes of 4 mm. The electric field lines (solid lines) are confined to the interior of the cell in this design making the measured conductivity (and instrument calibration) independent of objects near the cell.
From Sea-Bird ElectronicsConductivity, [math]C[/math], is found using the following formula:
[math]C=G\cdot kc , \qquad (4)[/math]
where [math]G[/math] is the conductance, and [math]kc[/math] is the cell constant. The cell constant is determined for a probe using the following formula:
[math]kc = \Large\frac{d}{A}\normalsize , \qquad (5)[/math]
where [math] d [/math] is the distance between the two electrodes, and [math]A[/math] is the area of the electrode surface. The conductivity value is found by multiplying conductance and the cell constant.
A potential difference is applied to the two probe electrodes in the Salinity Sensor. The resulting current is proportional to the conductivity of the solution. This current is converted into a voltage.
Electrodeless Conductivity Sensor (Inductive)

Inductive conductivity sensor principle
Electrodeless conductivity sensors use inductive coils. The inductive conductivity sensor consists of two coils which are incorporated next to one another in a polymer or ceramic body. These coils form current transformers. The sensor is designed so part of the liquid media forms a closed conductive current path passing through the coils. Current is applied to the primary coil (generating coil), which induces an alternating voltage in the liquid loop. In liquids which conduct electricity, this causes a current flow captured by the second coil (receiving coil), which is proportional to the conductivity of the sample solution.
Comparing the sensors
Electrode Sensors
- The main advantages of electrode sensors are:
- there is no proximity effect, the sensor can be mounted next to other sensors without interference
- easily calibrated in small baths
- The main disadvantages are:
- any changes in the cell constant will be reflected in the conductivity, and the cell cannot be cleaned in the field
- electrodes are subject to corrosion or damage (however, most sensors used in oceanography are inside a cell that prevents this, as shown in the image above)
- electrodes inside a cell need seawater pumping which limits the measuring rate
Inductive Sensors
- The main advantages of inductive sensors are:
- robust construction
- they can be cleaned with soap or solvents and a brush.
- there are no electrodes, so there is no possibility of their damage.
- The main disadvantages are:
- a significant part of the measurement is external leading to major consequences resulting from this external field. The inductive sensors require a 3 inches radius from any other surface, from adjacent sensors. It is particularly difficult to address this problem in companion mounts such as ARGO floats or biological fouling.
- mounting and calibration of the sensor to companion packages (Argo floats, current meters, AUVs, etc.) must be undertaken to avoid intrusion into the external area. Because final package geometry influences the results, the calibration must be performed on the fully assembled package.
Calibration
- Zero Calibration Point: Simply perform this calibration point with the probe out of any liquid or solution (e.g., in the air). A very small voltage reading will be read. Call this value 0 ppt.
- Standard Solution Calibration Point: Place the Salinity Sensor into a standard solution (solution of known concentration). Wait for the displayed voltage to stabilize. Enter the value of the standard solution (e.g., 35).
Related articles
- Salinity
- Seawater density
- Instruments and sensors to measure environmental parameters


