Difference between revisions of "Osmosis"
Dronkers J (talk | contribs) |
Dronkers J (talk | contribs) |
||
| Line 44: | Line 44: | ||
According to kinetic gas theory, all molecules in a fluid are in random (Brownian) motion with the same kinetic energy <math> ½ m v^2</math>, where <math>m</math> is the mass and <math>v^2</math> the mean squared velocity of a molecule. This means that large heavy molecules move more slowly than small light molecules. Mutual hitting of molecules generates a pressure <math>p</math> in the fluid, which is proportional to the kinetic energy of the molecules. According to the ideal gas law, the pressure is proportional to the temperature <math>T</math> (degrees Kelvin <math>[K]</math>) of the fluid, <math>p=(N/V) R \, T</math>, where <math>V=</math> volume, <math>N=</math> number of moles and <math>R \approx</math> 8.3 [J/K.mol] is the ideal gas constant. Small, light and fast particles passing the membrane exert a pressure on the molecules at the other side of the membrane, which exert a similar counterpressure if no large, heavy and slow particles are present on that side. In this case there is no pressure gradient across the membrane and the flow of molecules will be the same in both directions. However, large, heavy and slow molecules present at the opposite side of the membrane, will exert a lower counterpressure on the small, light and fast molecules passing the membrane<ref>Kiil, F. 1982. Mechanism of osmosis. Kidney International 21: 303—308</ref>. The osmotic pressure, <math>\Pi</math>, which is equal to the pressure drop <math>\Delta p</math> across the membrane, is therefore proportional to the molar concentration <math>c </math> [mole/l] of large, heavy and slow molecules and to the kinetic energy or temperature, <math>\Pi \propto c T</math>. The exact formula is <math>\Pi = c R T \;</math> [kPa]. | According to kinetic gas theory, all molecules in a fluid are in random (Brownian) motion with the same kinetic energy <math> ½ m v^2</math>, where <math>m</math> is the mass and <math>v^2</math> the mean squared velocity of a molecule. This means that large heavy molecules move more slowly than small light molecules. Mutual hitting of molecules generates a pressure <math>p</math> in the fluid, which is proportional to the kinetic energy of the molecules. According to the ideal gas law, the pressure is proportional to the temperature <math>T</math> (degrees Kelvin <math>[K]</math>) of the fluid, <math>p=(N/V) R \, T</math>, where <math>V=</math> volume, <math>N=</math> number of moles and <math>R \approx</math> 8.3 [J/K.mol] is the ideal gas constant. Small, light and fast particles passing the membrane exert a pressure on the molecules at the other side of the membrane, which exert a similar counterpressure if no large, heavy and slow particles are present on that side. In this case there is no pressure gradient across the membrane and the flow of molecules will be the same in both directions. However, large, heavy and slow molecules present at the opposite side of the membrane, will exert a lower counterpressure on the small, light and fast molecules passing the membrane<ref>Kiil, F. 1982. Mechanism of osmosis. Kidney International 21: 303—308</ref>. The osmotic pressure, <math>\Pi</math>, which is equal to the pressure drop <math>\Delta p</math> across the membrane, is therefore proportional to the molar concentration <math>c </math> [mole/l] of large, heavy and slow molecules and to the kinetic energy or temperature, <math>\Pi \propto c T</math>. The exact formula is <math>\Pi = c R T \;</math> [kPa]. | ||
| − | The osmotic pressure can be very high. For example, | + | The osmotic pressure can be very high. For example, the osmotic pressure across a semipermeable membrane separating fresh water and seawater (35 g NaCl/l , <math>\; c \approx </math> 1.2 mole NaCL/l), is <math>\Pi \approx </math> 30,000 kPa =30 bar. |
Latest revision as of 12:27, 29 April 2024
Definition of Osmosis:
The diffusion of water through a semipermeable membrane from a solution with a lower to one with a higher solute concentration. [1]
This is the common definition for Osmosis, other definitions can be discussed in the article
|
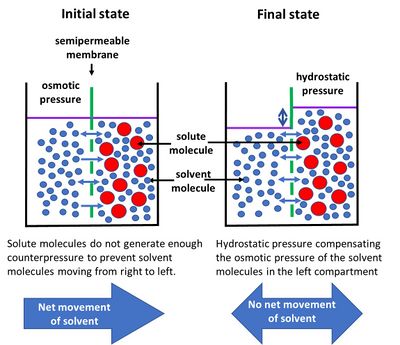
Osmosis is a phenomenon of selective passage of different molecules through a semipermeable membrane, resulting in a net influx to the membrane side with the highest concentration of blocked molecules. This influx stops when a sufficient pressure difference has built up between the compartments on either side of the membrane. The principle, based on the interaction between the different molecules and the membrane, is explained in the accompanying figure[2]. Here, two compartments with a free surface are separated by a membrane. On one side there is a liquid with small and light molecules that can cross the membrane (e.g. a solvent, such as water) and on the other side a solution containing large and heavy molecules that cannot cross the membrane (e.g. solutes, such as salt ions dissolved in water). The solute molecules, which are heavier and therefore moving more slowly than the solvent molecules, form a barrier, preventing the solvent molecules in the solution from generating a neutralizing counterpressure for the molecules passing the membrane from the other side. The resulting net inflow of solvent molecules through the membrane increases the pressure in the solution compartment until an equilibrium is reached where the net solvent inflow is eventually neutralized.
Osmosis is an essential process for the cells of living organisms. The permeability of the cell membrane allows the uptake of molecules from the environment that are necessary for the cells to function. However, the cell membrane does not allow the passage of all substances. Osmosis therefore can induce a net uptake of ambient fluid or a net loss of cell fluid, depending on the tonicity of the ambient fluid. To prevent expansion or shrinkage of cells, cells use different mechanisms to maintain a balance between water and solutes in their bodies. This is called homeostasis.
Contents
Related definitions[3]
Osmolality
The concentration of a solute that induces osmotic pressure, expressed in osmols per kilogram of solvent.
Osmolyte
Organic molecules that keep intracellular fluids at the same osmotic pressure as the marine environment to avoid cell shrinkage or dilatation. Osmolytes are usually low-weight organic molecules such as sugars, amino acids or methylamines.
Isosmotic intracellular regulation
Cellular mechanisms that, upon a change in surrounding salinity, lead to the adjustment of the intracellular osmotic pressure to meet that of the environment, thus minimizing variations in cell hydration. Adjustment of the intracellular osmotic pressure usually occurs through the production of organic osmolytes.
Anisosmotic extracellular osmoregulation
Mechanisms acting to maintain body (extracellular) fluid volume, osmotic pressure and ionic composition despite environmental salinity changes.
Osmoregulators
Species that carry out anisosmotic extracellular regulation when exposed to extracellular osmolality changes. This is achieved through several mechanisms involving various permeability and salt transport properties within different ion-transporting epithelia. Osmoregulators finally restore the salt balance through excretion of excess salt or excess water.
Osmoconformers
Species that maintain their internal medium isosmotic to their environment, minimizing water fluxes across membranes. Osmoconformers that are adapted to varying salinity usually maintain equal osmotic pressure through the production of organic osmolytes.
Tonicity
- Hypertonicity is the presence of a solution that causes cells to shrink.
- Hypotonicity is the presence of a solution that causes cells to swell.
- Isotonicity is the presence of a solution that produces no change in cell volume.
Appendix Molecular interpretation of osmosis and formula
According to kinetic gas theory, all molecules in a fluid are in random (Brownian) motion with the same kinetic energy [math] ½ m v^2[/math], where [math]m[/math] is the mass and [math]v^2[/math] the mean squared velocity of a molecule. This means that large heavy molecules move more slowly than small light molecules. Mutual hitting of molecules generates a pressure [math]p[/math] in the fluid, which is proportional to the kinetic energy of the molecules. According to the ideal gas law, the pressure is proportional to the temperature [math]T[/math] (degrees Kelvin [math][K][/math]) of the fluid, [math]p=(N/V) R \, T[/math], where [math]V=[/math] volume, [math]N=[/math] number of moles and [math]R \approx[/math] 8.3 [J/K.mol] is the ideal gas constant. Small, light and fast particles passing the membrane exert a pressure on the molecules at the other side of the membrane, which exert a similar counterpressure if no large, heavy and slow particles are present on that side. In this case there is no pressure gradient across the membrane and the flow of molecules will be the same in both directions. However, large, heavy and slow molecules present at the opposite side of the membrane, will exert a lower counterpressure on the small, light and fast molecules passing the membrane[4]. The osmotic pressure, [math]\Pi[/math], which is equal to the pressure drop [math]\Delta p[/math] across the membrane, is therefore proportional to the molar concentration [math]c [/math] [mole/l] of large, heavy and slow molecules and to the kinetic energy or temperature, [math]\Pi \propto c T[/math]. The exact formula is [math]\Pi = c R T \;[/math] [kPa].
The osmotic pressure can be very high. For example, the osmotic pressure across a semipermeable membrane separating fresh water and seawater (35 g NaCl/l , [math]\; c \approx [/math] 1.2 mole NaCL/l), is [math]\Pi \approx [/math] 30,000 kPa =30 bar.
External links
Wikipedia articles Osmosis and Osmotic pressure.
References
- ↑ Pinet P.R. 1998. Invitation to Oceanography. Jones and Barlett Publishers. p. 508
- ↑ Nelson, P.G. 2017. Osmosis and thermodynamics explained by solute blocking. Eur. Biophys. J. 46: 59–64
- ↑ Rivera-Ingraham, G.A. and Lignot, J-H. 2017. Osmoregulation, bioenergetics and oxidative stress in coastal marine invertebrates: raising the questions for future research. Journal of Experimental Biology 220: 1749-1760
- ↑ Kiil, F. 1982. Mechanism of osmosis. Kidney International 21: 303—308
Please note that others may also have edited the contents of this article.
|