Difference between revisions of "Light fields and optics in coastal waters"
(→Optical closure) |
Dronkers J (talk | contribs) |
||
| (67 intermediate revisions by 8 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | ||
| + | The quantitative study of underwater light fields in coastal waters and shelf seas has important applications in ecology, engineering and [[remote sensing]]. This article introduces the theoretical basis of optical measurements. Attention is paid to descriptors of light fields, optical properties of natural waters and light field modelling. For more information about the measurement of light fields, see also the article [[Optical measurements in coastal waters]]. | ||
==Introduction of underwater light fields== | ==Introduction of underwater light fields== | ||
| Line 7: | Line 8: | ||
# play an important role in determining rates of photosynthesis by phytoplankton and macrophytes, and therefore set limits on the productivity of marine ecosystems. | # play an important role in determining rates of photosynthesis by phytoplankton and macrophytes, and therefore set limits on the productivity of marine ecosystems. | ||
# influence the range at which objects are visible under water, which is of great significance for diving and engineering operations and also for visual interactions between predators and prey species. | # influence the range at which objects are visible under water, which is of great significance for diving and engineering operations and also for visual interactions between predators and prey species. | ||
| − | # determine the volume reflectance of seawater which is important for optical remote sensing. | + | # determine the volume reflectance of seawater which is important for [[optical remote sensing]]. |
===Dynamics of underwater light fields=== | ===Dynamics of underwater light fields=== | ||
| − | Variations in underwater light fields originate from changes in both solar illumination and seawater composition, and predicting this variability involves the study of radiative transfer in an optically complex medium. There is an extensive literature on underwater light fields and associated problems in marine optics, but the fundamental concepts are clearly laid out in the books by Kirk (1994<ref name="kirk"> | + | Variations in underwater light fields originate from changes in both solar illumination and seawater composition, and predicting this variability involves the study of radiative transfer in an optically complex medium. There is an extensive literature on underwater light fields and associated problems in marine optics, but the fundamental concepts are clearly laid out in the books by Kirk (1994<ref name="kirk">Kirk J T O 1994 Light and photosynthesis in aquatic ecosystems. Cambridge University Press, Cambridge, 410 pp.</ref>), Mobley (1994<ref name="mob">Mobley C D 1994 Light and water; radiative transfer in natural waters. Academic Press, San Diego, 592pp. ISBN 0125027508</ref>) and Bukata et al (1995<ref>Bukata R P, Jerome J H , Kondratyev K Y and Pozdnyakov D V 1995 Optical properties and remote sensing of inland and coastal waters. CRC Press, 384pp</ref>). One of the challenges posed by coastal light fields is the potential for interaction and between physical and biological factors. For example, sediment particles in suspension can limit the illumination of benthic photosynthetic organisms, but the presence of those organisms may stabilise the sediment surface and reduce the probability of sediment re-suspension taking place. |
| − | Kirk J T O 1994 Light and photosynthesis in aquatic ecosystems. Cambridge University Press, Cambridge, 410 pp.</ref>), Mobley (1994<ref name="mob">Mobley C D 1994 Light and water; radiative transfer in natural waters. Academic Press, San Diego, 592pp. ISBN 0125027508</ref>) and Bukata et al (1995<ref>Bukata R P, Jerome J H , Kondratyev K Y and Pozdnyakov D V 1995 Optical properties and remote sensing of inland and coastal waters. CRC Press, 384pp</ref>). One of the challenges posed by coastal light fields is the potential for interaction and between physical and biological factors. For example, sediment particles in suspension can limit the illumination of benthic photosynthetic organisms, but the presence of those organisms may stabilise the sediment surface and reduce the probability of sediment re-suspension taking place. | ||
Underwater light fields are vulnerable to human activities. Anthropogenic disturbances such as eutrophication, dredging operations and accelerated soil erosion due to the de-afforestation of river catchments can modify underwater light climates in coastal regions. Increases in [[turbidity]] produced by these activities can damage important ecosystem components such as coral reefs and sea grass beds. | Underwater light fields are vulnerable to human activities. Anthropogenic disturbances such as eutrophication, dredging operations and accelerated soil erosion due to the de-afforestation of river catchments can modify underwater light climates in coastal regions. Increases in [[turbidity]] produced by these activities can damage important ecosystem components such as coral reefs and sea grass beds. | ||
The underwater light field depends on: | The underwater light field depends on: | ||
| − | # | + | # <u>the optical characteristics of sea water</u>: The optical characteristics of coastal waters are determined not only by water itself, but also by suspended particulate material (minerals, organic detritus and phytoplankton) and coloured dissolved organic matter. The presence of relatively high concentrations of dissolved organic matter or minerals often distinguishes coastal waters from those of deeper seas, and accounts for their green or brown colouration. |
| − | # | + | # <u>the conditions of illumination</u>: The conditions of illumination depend on solar angle, the degree and type of cloud cover, and the state of the sea surface. As a result, underwater light fields show strong diurnal and seasonal variability. |
| − | == | + | ==Light field descriptors== |
===Radiance and irradiance=== | ===Radiance and irradiance=== | ||
| − | '''[http://en.wikipedia.org/wiki/Radiance Radiance]''' is the fundamental quantity in light field measurement. It is usually denoted L(q,f, | + | '''[http://en.wikipedia.org/wiki/Radiance Radiance]''' is the fundamental quantity in light field measurement. It is usually denoted <math>L(q,f,\lambda)</math> where the angles <math>q</math> (zenith) and <math>f</math> (azimuth) specify the direction in which the radiance is measured and <math>\lambda</math> is the wavelength. The units of radiance are W m<sup>-2</sup> nm<sup>-1</sup> sr<sup>-1</sup>. Measurements of the water-leaving radiance <math>L_w</math> just above the surface at <math>q = 0</math> (nadir viewing) are particularly important for [[remote sensing]]. |
| − | '''Planar and scalar [http://en.wikipedia.org/wiki/Irradiance irradiances]''' | + | '''Planar and scalar [http://en.wikipedia.org/wiki/Irradiance irradiances]''' <math>E_x(\lambda)</math> are generated by integrating radiances over defined intervals of solid angle <math>D_w</math>. They have units of W m<sup>-2</sup> nm<sup>-1</sup>. For planar irradiances, the radiances are multiplied by the cosine of their angle of incidence on the detecting plane before carrying out the integration. Scalar irradiances omit the cosine weighting. Measurements of planar irradiances are made using a diffusing disc as a collector, while scalar irradiances are measured use a diffusing sphere. Commonly used irradiances are summarized Table 1. |
| − | {| border="1" width="600px" | + | {| border="1" width="600px" cellspacing="0" |
| − | |+ Table 1: Commonly used irradiances | + | |+ '''Table 1: Commonly used irradiances''' |
|- | |- | ||
! Quantity | ! Quantity | ||
| Line 33: | Line 33: | ||
! Angular limits | ! Angular limits | ||
|- | |- | ||
| − | | | + | | <math>E_{\theta}(\lambda)</math> |
| Scalar irradiance | | Scalar irradiance | ||
| whole sphere | | whole sphere | ||
|- | |- | ||
| − | | [ | + | | <math>[E_{\theta}(\lambda]_u</math> |
| Upward scalar irradiance | | Upward scalar irradiance | ||
| lower hemisphere | | lower hemisphere | ||
|- | |- | ||
| − | | [ | + | | <math>[E_{\theta}(\lambda]_d</math> |
| Downward scalar irradiance | | Downward scalar irradiance | ||
| upper hemisphere | | upper hemisphere | ||
|- | |- | ||
| − | | | + | | <math>E_u(\lambda)</math> |
| Upward planar irradiance | | Upward planar irradiance | ||
| lower hemisphere | | lower hemisphere | ||
|- | |- | ||
| − | | | + | | <math>E_d(\lambda)</math> |
| Downward planar irradiance | | Downward planar irradiance | ||
| upper hemisphere | | upper hemisphere | ||
|} | |} | ||
| − | A full description of an underwater light field would involve the specification of the spectral and angular distribution of radiance as a function of depth and geographical location, but this degree of detail is impractically cumbersome. The quantities most frequently specified are upward radiances and upward and downward irradiances. | + | A full description of an underwater light field would involve the specification of the spectral and angular distribution of radiance as a function of depth and geographical location, but this degree of detail is impractically cumbersome. The quantities most frequently specified are upward radiances and upward and downward irradiances. |
===Wavelength ranges=== | ===Wavelength ranges=== | ||
| Line 61: | Line 61: | ||
===Measurement units=== | ===Measurement units=== | ||
Three systems of units may be encountered in the literature on underwater light fields: | Three systems of units may be encountered in the literature on underwater light fields: | ||
| − | # | + | # <u>Radiometric units</u>: In physical radiometry, light energy is measured in joules (J), radiometric power in watts (W or J s<sup>-1</sup>), and the source brightness as power per unit solid angle (W sr<sup>-1</sup>). |
| − | # | + | # <u>Quantum units</u>: In photochemistry and photobiology, where molecular events are driven by the absorption of individual quanta, it is often useful to measure light fields in terms of numbers of photons rather than energy. A convenient unit is the mol (Avogadro’s Number) of photons. In the photobiology literature, one mol of photons is often referred to as an einstein, but the unit is redundant. The energy associated with a single photon of a given wavelength in vacuo is <math>e = hc/\lambda</math>, where <math>h</math> is Planck’s constant and <math>c</math> the speed of light. The inverse wavelength dependence means that conversion between radiometric and quantum units (for example from W m<sup>-2</sup> s<sup>-1</sup> to mol photons m<sup>-2</sup> s<sup>-1</sup> in the case of irradiance) requires explicit knowledge of the spectral distribution of the light field. Integration of scalar quantum irradiance across the visible spectrum (400-700 nm) gives a measure of photosynthetically active radiation (PAR: mol photons m<sup>-2</sup> s<sup>-1</sup>). |
| − | # | + | # <u>Photometric units</u>: The visual effect of a given source of illumination depends on the spectral sensitivity of the human eye. This leads to a system of photometric units based on the lumen as the measurement of effective power, and is discussed in DeCusatis (1997<ref>DeCusatis C M (ed) 1997 Handbook of Applied Photometry. American Institute of Physics Press, New York, 484 pp.</ref>). Conversion between radiometric and photometric units has to take both the standard eye response curve and the spectral distribution of the light field into account. |
==Optical properties of natural waters== | ==Optical properties of natural waters== | ||
| Line 71: | Line 71: | ||
The optical characteristics of a light-transmitting medium can be specified in terms of its inherent optical properties, which represent the effect of an optically thin slab of the medium on the transmission of a collimated light beam. The main IOPs are summarized in table 2: | The optical characteristics of a light-transmitting medium can be specified in terms of its inherent optical properties, which represent the effect of an optically thin slab of the medium on the transmission of a collimated light beam. The main IOPs are summarized in table 2: | ||
| − | {| border="1" width=" | + | {| border="1" width="500px" cellspacing="0" |
| − | |+ Table 2: Main Inherent Optical Properties | + | |+ '''Table 2: Main Inherent Optical Properties''' |
|- | |- | ||
| − | | a | + | | <math>a</math> |
| absorption coefficient | | absorption coefficient | ||
| m<sup>-1</sup> | | m<sup>-1</sup> | ||
|- | |- | ||
| − | | b | + | | <math>b</math> |
| scattering coefficient | | scattering coefficient | ||
| m<sup>-1</sup> | | m<sup>-1</sup> | ||
|- | |- | ||
| − | | c = a + b | + | | <math>c = a + b</math> |
| attenuation coefficient | | attenuation coefficient | ||
| m<sup>-1</sup> | | m<sup>-1</sup> | ||
|- | |- | ||
| − | | | + | | <math>\beta</math> |
| scattering phase function | | scattering phase function | ||
| sr<sup>-1</sup> | | sr<sup>-1</sup> | ||
| Line 92: | Line 92: | ||
| − | Formal definitions for these IOPs may be found in Mobley (1994<ref name="mob"/>). The absorption, scattering and attenuation coefficients have fairly obvious meanings, while the phase function is a measure of the relative angular distribution of the scattered light. The scattering coefficient (b) is often partitioned into forward and backwards components, and the | + | Formal definitions for these IOPs may be found in Mobley (1994<ref name="mob"/>). The absorption, scattering and attenuation coefficients have fairly obvious meanings, while the phase function is a measure of the relative angular distribution of the scattered light. The scattering coefficient (b) is often partitioned into forward and backwards components, and the <u>backscattering coefficient (bb)</u> is of great importance for determining the [[remote sensing]] reflection of a water body. |
| − | The | + | The <u>total IOPs</u> of a body of seawater can be considered as the sum of the partial contributions from water itself and a number of optically significant constituents. These constituents are generally divided into four classes: |
#Phytoplankton cells and colonies (Phyt) | #Phytoplankton cells and colonies (Phyt) | ||
| Line 101: | Line 101: | ||
#Organic suspended solids or detritus (OSS) | #Organic suspended solids or detritus (OSS) | ||
| − | The concentration of the photosynthetic pigment chlorophyll a (Chl, mg m<sup>-3</sup>) is often used as a proxy variable for phytoplankton biomass. Mineral particle and organic detritus concentrations (g m<sup>-3</sup>) are determined by filtering water samples through a fine glass fibre filter and measuring the dry weight of material retained before and after combusting the filter at | + | The concentration of the photosynthetic pigment chlorophyll a (Chl, mg m<sup>-3</sup>) is often used as a proxy variable for phytoplankton biomass. Mineral particle and organic detritus concentrations (g m<sup>-3</sup>) are determined by filtering water samples through a fine glass fibre filter and measuring the dry weight of material retained before and after combusting the filter at 500°C to remove the organic portion. Since there is no standard method for measuring the mass concentration of coloured dissolved organic matter, it is conventionally measured as the absorption coefficient at 440 nm of seawater which has been passed through a membrane filter with a 0.2 μm pore size. |
The total absorption coefficient can be written as the sum of the contributions of the individual constituents: | The total absorption coefficient can be written as the sum of the contributions of the individual constituents: | ||
| Line 107: | Line 107: | ||
<math>a_{total} = a_{water}\, +\, a_{Phyt}\, +\, a_{MSS}\, +\, a_{CDOM}\, +\, a_{OSS} </math> | <math>a_{total} = a_{water}\, +\, a_{Phyt}\, +\, a_{MSS}\, +\, a_{CDOM}\, +\, a_{OSS} </math> | ||
| − | The scattering coefficient (b), attenuation coefficient (c) and phase function ( | + | The scattering coefficient (<math>b</math>), attenuation coefficient (<math>c</math>) and phase function (<math>\beta</math>) can all be partitioned in a similar manner. In practice, however, the optical contributions of these four classes of material may not be completely distinct: [[algal bloom|blooms]] formed by phytoplankton groups such as coccolithophores and diatoms may generate significant concentrations of mineral particles (calcite and silica respectively), and organic detrital material may form flocs which incorporate suspended minerals. |
===Specific optical properties and characteristics of constituents=== | ===Specific optical properties and characteristics of constituents=== | ||
The optical contributions of the main classes of constituents can be calculated by multiplying the concentrations of each constituent by the value of its inherent properties expressed per unit concentration. The latter quantity is often referred to as a specific inherent optical property or specific optical cross section. For example: | The optical contributions of the main classes of constituents can be calculated by multiplying the concentrations of each constituent by the value of its inherent properties expressed per unit concentration. The latter quantity is often referred to as a specific inherent optical property or specific optical cross section. For example: | ||
| − | <math>a_{MSS} = MSS \times a*MSS</math> | + | <math>a_{MSS} = MSS \times a^*(MSS)</math> |
| − | where MSS is the concentration of suspended minerals and a*MSS is the specific absorption cross section for this constituent, with units of m<sup>2</sup> g<sup>-1</sup>. | + | where <math>MSS</math> is the concentration of suspended minerals and <math>a^*(MSS)</math> is the specific absorption cross section for this constituent, with units of m<sup>2</sup> g<sup>-1</sup>. The convention that seawater contains four classes of optically significant constituents tends to conceal the fact that there can be considerable variability in specific optical properties within each class of constituent. Moreover, optical characterisation of the four main classes of constituent is currently incomplete. |
| + | <br> | ||
| − | The | + | :<u>''Phytoplankton cells and colonies (Phyt)''</u>: A great deal of effort has been devoted to the study of the absorption and scattering characteristics of phytoplankton cells (see for example Sathyendranath et al 1987<ref>Sathyendranath S, Lazzara L, Prieur L 1987 Variations in the Spectral Values of Specific Absorption of Phytoplankton. Limnology and Oceanography 32: 403-415</ref>, Bricaud et al 1988<ref>Bricaud, A., Bedhomme, A.L. and A. Morel (1988). Optical properties of diverse phytoplanktonic species: Experimental results and theoretical interpretation, Journal of Plankton Research, 10, 851-873</ref> and Johnsen et al 1994<ref>Johnsen G, Samset O, Grauskog L and Sakshaug E 1994 In vivo absorption characteristics in 10 classes of bloom-forming phytoplankton: taxonomic characteristics and responses to photoadaptation by means of discriminant and HPLC analysis. Marine Ecology Progress Series 105:149-157</ref>). The absorption spectra generally show maxima around the main chlorophyll absorption peaks at 440 nm and 675 nm, with subsidiary features depending on the presence of accessory light harvesting and photoprotective pigments. Phytoplankton scattering poses considerable practical and theoretical challenges because of the wide range of size and structure exhibited by individual cells and colonies. A helpful review of the theoretical problems is given by Quirantes and Bernard (2004<ref>Quirantes A and Bernard S 2004 Light scattering by marine algae: two-layer spherical and nonspherical models. Journal of Quantitative Spectroscopy & Radiative Transfer 89: 311–321</ref>) and measurement issues are discussed in Volten et al.(1998<ref>Volten H, de Haan J F , Hovenier J W, Scheurs R, Vassen W, Dekker A G, Hoogenboom H J, Charlton F and Wouts R. 1998 Laboratory measurements of angular distributions of light scattered by phytoplankton and silt. Limnology and Oceanography 43: 1180-1197.</ref>). For all but the smallest species, phytoplankton scattering is strongly peaked in the forward direction. One interesting feature in the total scattering spectra is the presence of minima near the chlorophyll absorption peaks which is due to Kettler-Helmholtz anomalous dispersion. There is some evidence that the specific backscattering coefficients of most phytoplankton species are too low to account for the magnitude of water-leaving radiance signals observed from natural populations, but measurements in this area are imprecise and current theoretical models do not take the full structural complexity of phytoplankton cells into account. |
| + | :<u>''Mineral suspended solids (MSS)''</u>: The optics of some types of mineral particles have been systematically explored (Babin and Stramski 2005<ref>Babin M., and Stramski D 2005 Variations in the mass-specific absorption coefficient of mineral particles suspended in water. Limnology and Oceanography, 49, 756-767</ref>). Their absorption spectra are generally high in the blue wavebands and decrease towards the red, and for field samples their shape is often similar to that for CDOM. Scattering characteristics are influenced by size distribution and refractive index (Wozniak and Stramski 2004<ref>Wozniak, Slawomir B.; Stramski, Dariusz 2004 Modeling the Optical Properties of Mineral Particles Suspended in Seawater and their Influence on Ocean Reflectance and Chlorophyll Estimation from Remote Sensing Algorithms Applied Optics IP, vol. 43, Issue 17, pp.3489-3503</ref>). It is not clear whether laboratory samples of mineral dusts are representative of all the materials found in coastal locations. | ||
| + | :<u>''Coloured dissolved organic matter (CDOM)''</u> CDOM absorption has been extensively characterised. It is generally described by an exponential function of the form: <math>a(\lambda\,)_{cdom}=a(\lambda_{\theta})_{cdom}\, e^{-S(\lambda - \lambda_{\theta})}</math>. In which: <math>\lambda_{\theta}</math> is a reference wavelength (usually 440 nm) and <math>S</math> is a coefficient which has a typical value of 0.01 to 0.02 in UK coastal waters (Bricaud et al 1981<ref>Bricaud A, Morel A and Prieur L 1981 Absorption by dissolved organic matter of the sea (yellow substance) in the UV and visible domains. Limnology and Oceanography 26:43-53.</ref>). Light scattering by CDOM is generally assumed negligible, but it is possible that some of the coloured material passing through 0.2 μm filters is colloidal in nature and therefore capable of contributing to the total scattering coefficient. | ||
| + | :<u>''Organic suspended solids or detritus (OSS)''</u>: The optical properties of organic detritus are not well characterised. This is due to the wide range of material which falls under this classification, ranging from scenescent phytoplankton cells to faecal pellets in offshore waters and including terrestrial vegetable matter in estuaries. There is also the possibility that organic matter may form flocs which include mineral particles in estuaries and in post-bloom shelf-sea conditions. | ||
| − | + | ===Other relevant parameters=== | |
| − | + | Changes in light field parameters with depth (<math>z</math>) are often approximately exponential in nature. For example, the attenuation of downward planar irradiance in a uniform water column can be written: | |
| − | |||
| − | |||
| − | |||
| − | = | + | <math>E_d(\lambda, z) = E_d (\lambda, \theta)e^{-K_d z}</math>, |
| − | |||
| − | <math> | + | in which <math>K_d</math> is the vertical attenuation coefficient. Quantities such as <math>K_d</math> are relatively insensitive to input conditions at moderate solar angles and are frequently referred to as <u>apparent optical properties (AOPs)</u> (Kirk 1994<ref name="kirk"/>). Some examples of AOPs are: |
| − | + | * The attenuation coefficient for downwards planar irradiance (<math>K_d</math>) | |
| − | + | * The attenuation coefficient for scalar irradiance (<math>K_{\theta}</math>) | |
| − | * The attenuation coefficient for downwards planar irradiance ( | + | * Irradiance reflectance (<math>R</math>) |
| − | * The attenuation coefficient for scalar irradiance ( | + | * [[Remote sensing]] reflectance (measured just above the sea surface) (<math>R_{rs}</math>) |
| − | * Irradiance reflectance (R) | + | * The mean cosine (<math>\mu</math>) |
| − | * [[Remote sensing]] reflectance (measured just above the sea surface) ( | ||
| − | * The mean cosine ( | ||
[[image:uw_optics01.jpg|thumb|right|350px|Figure 1: Measurements of PAR at three contrasting stations in the Irish Sea in April (station 10) and November (stations 26 and 29)]] | [[image:uw_optics01.jpg|thumb|right|350px|Figure 1: Measurements of PAR at three contrasting stations in the Irish Sea in April (station 10) and November (stations 26 and 29)]] | ||
| − | + | <u>Photosynthetically available radiation (PAR)</u> is the integral of scalar irradiance, expressed in quantum units, over the 400 -700 nm waveband. The term <math>K_{PAR}</math>, defined by analogy with <math>K_{\theta}</math> and <math>K_d</math>, is sometimes used to describe the attenuation of PAR. However since the attenuation of light by seawater varies with wavelength, the reduction in PAR with depth can deviate from the exponential approximation in the upper part of the water column. Figure 1 shows the measured variability of PAR with depth for three contrasting stations in the Irish Sea. | |
| − | The | + | The optical depth <math>z(\lambda;l)</math> is defined as the depth at which <math>E_d</math> is reduced to 1/e (~0.37) of its value immediately below the surface. This quantity is wavelength-dependent, as might be expected from the fact that the spectral distribution of the underwater light field changes with depth. The maximum depth at which significant photosynthesis can occur (the euphotic depth, <math>z_{eu}</math>) is conventionally taken to be the point at which PAR is reduced to 1% of its surface value (Kirk 1994<ref name="kirk"/>). |
| − | The | + | The <u>horizontal range of visibility</u> (<math>y</math>) at which a black target is judged to be visible to a human observer is empirically related to the attenuation coefficient <math>c</math> by the relationship: |
| − | : <math>y\, = | + | : <math>y\, = 4.8 / c </math> . |
A theoretical basis for this relationship, based on radiance transfer theory, is given by Zaneveld and Pegau (2003<ref>Zaneveld J R V and Pegau W S 2003 Robust underwater visibility parameter. Optics Express 11:2997-3009</ref>). | A theoretical basis for this relationship, based on radiance transfer theory, is given by Zaneveld and Pegau (2003<ref>Zaneveld J R V and Pegau W S 2003 Robust underwater visibility parameter. Optics Express 11:2997-3009</ref>). | ||
| Line 149: | Line 147: | ||
==Radiative transfer theory and light field modelling== | ==Radiative transfer theory and light field modelling== | ||
===The radiative transfer equation=== | ===The radiative transfer equation=== | ||
| − | The propagation of light energy through a medium which absorbs, scatters and contains internal sources is determined by the radiative transfer equation, which is widely used in fields such as astronomy and atmospheric science as well as hydrological optics (Goody and Yung 1989<ref>Goody R M and Yung Y L 1989 Atmospheric radiation, theoretical basis. Oxford University Press, Oxford. 519pp.</ref>). In marine light fields, sunlight enters from above and is attenuated with depth (z). In the simple case where bottom reflectance can be neglected and the water is horizontally homogeneous, the change in monochromatic radiance in a given direction (q,f) as a function of depth ( | + | The propagation of light energy through a medium which absorbs, scatters and contains internal sources is determined by the radiative transfer equation, which is widely used in fields such as astronomy and atmospheric science as well as hydrological optics (Goody and Yung 1989<ref>Goody R M and Yung Y L 1989 Atmospheric radiation, theoretical basis. Oxford University Press, Oxford. 519pp.</ref>). In marine light fields, sunlight enters from above and is attenuated with depth (<math>z</math>). In the simple case where bottom reflectance can be neglected and the water is horizontally homogeneous, the change in monochromatic radiance in a given direction (<math>q,f</math>) as a function of depth (<math>z</math>) is given by |
| − | |||
| − | <math> | ||
| − | + | <math>\Large\frac{d L(z,q,f)}{dr}\normalsize = -cL(z,q,f) + L^*(z,q,f)+ S(z,q,f)</math>, | |
| − | [[image:uw_optics02. | + | in which: <math>L^*(z,q,f)</math> represents the gain in radiance due to light scattered from adjacent paths and <math>S(z,q,f)</math> accounts for any internal sources. In coastal waters, the most important internal source terms arise from Raman scattering by water molecules and fluorescence from dissolved organic matter and phytoplankton pigments. For light-field modelling the radiative transfer equation is solved numerically using either Monte Carlo methods or more conceptually sophisticated mathematical techniques (Mobley 1994<ref name="mob"/>, Thomas and Stamnes 1999<ref>Thomas G E.and Stamnes K 1999 Radiative transfer in the atmosphere and ocean, Cambridge, New York, Cambridge University Press 517 p., ISBN 0521401240.</ref>). The discrete ordinates method is commonly used in optical oceanography and is implemented in the commercially available Hydrolight software package (Sequoia Scientific). In order to construct a light field model, it is necessary to specify the nature of the input illumination, the IOPs of the medium, and any internal source functions (Figure 2). Light field models can generate a complete set of radiance values, but their output is usually summarised as a set of AOPs and reflectances which corresponds to those most frequently measured. |
| + | [[image:uw_optics02.jpg|thumb|centre|750px|Figure 2: Input/output relationships for the numerical modelling of radiative transfer in shelf seas.]] | ||
===Optical closure=== | ===Optical closure=== | ||
| − | Ideally, it should be possible to construct a light field model of a coastal water column using measured values of the IOPs which would precisely replicate radiometric measurements made at the same time. This is known as | + | Ideally, it should be possible to construct a light field model of a coastal water column using measured values of the IOPs which would precisely replicate radiometric measurements made at the same time. This is known as <u>‘optical closure’</u>. It is difficult to achieve in practice for two main reasons. First, it places great demands on the appropriate calibration and deployment of the measuring instruments. Second, some key IOPs such as the scattering phase function are difficult to measure [[in situ]], and are usually estimated from the backscattering ratio (bb/b) using analytical functions. Figure 3 shows a typical attempt to achieve optical closure for a shelf sea station in the Irish Sea with constituent concentrations of: Chl 1.6 mg m<sup>-3</sup>, MSS 1.9 mg l<sup>-1</sup>, CDOM a440 0.2m<sup>-1</sup>. In this instance the match between measured and modelled <math>E_d</math> values is reasonably good, but the <math>L_u</math> plots diverge significantly below 5 m. The symbols in Figure 3 represent measurements made with a profiling radiometer (Satlantic SPMR) and are spaced at 1 m intervals from the sea surface. The lines indicate the output of Hydrolight calculations of downward irradiance (upper plot) and upward radiance (lower plot) which used [[in-situ]] measurements of IOPs as inputs. Absorption and scattering coefficients were measured using a dual tube photometer (Wet Labs ac-9) and backscattering coefficients measured using a Hydroscat 2 (HobiLabs) backscattering meter. |
| − | < | + | <blockquote style="background: rgb(245, 245, 245); border: 1px solid rgb(153, 153, 153);padding: 1em; width:600px; margin:0 auto"> |
| − | + | {| | |
| − | + | |- | |
| − | + | | width=300px| [[image:uw_optics03a.jpg|300px]] | |
| − | + | | width=300px| [[image:uw_optics03b.jpg|300px]] | |
| − | + | |- | |
| − | + | |+ align="bottom" style="caption-side: bottom; text-align: left;" | Figure 3: Typical results of an attempt to achieve optical closure for a station in the Irish Sea. | |
| − | + | |} | |
| − | + | </blockquote> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | ||
| − | |||
| − | |||
| − | [[image: | ||
| − | |||
| − | [[image: | ||
| − | |||
| − | |||
| − | |||
| − | == | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==See also== | ==See also== | ||
| Line 223: | Line 181: | ||
==References== | ==References== | ||
| + | |||
<references/> | <references/> | ||
| − | { | + | <div style = "float: center"> |
| − | | | + | {| style="border:1px solid #abd5f5; background:#f1f5fc; margin:0em 0em 0em 5em;" |
| − | + | |<center>The main authors of this article are [http://www.coastalwiki.org/imis/imis.php?module=person&persid=14356 Alex Cunningham] and Leanne Ramage<br><small>Please note that others may also have edited the contents of this article. </small> </center> | |
| − | + | ---- | |
| + | |||
| + | * For other articles by this author see [[:Category:Articles by Leanne Ramage]] | ||
| + | * For other articles by this author see [[:Category:Articles by Alex Cunningham]] | ||
| + | * For an overview of contributions by this author see [[Special:Contributions/Alex.cunningham]] | ||
| + | |} | ||
| − | + | [[Category:Articles by Alex Cunningham]] | |
| − | + | [[Category:Articles by Leanne Ramage]] | |
| − | + | </div> | |
| − | [[Category: | + | [[Category:Coastal and marine observation and monitoring]] |
| − | |||
| − | |||
Latest revision as of 19:41, 19 August 2020
The quantitative study of underwater light fields in coastal waters and shelf seas has important applications in ecology, engineering and remote sensing. This article introduces the theoretical basis of optical measurements. Attention is paid to descriptors of light fields, optical properties of natural waters and light field modelling. For more information about the measurement of light fields, see also the article Optical measurements in coastal waters.
Contents
Introduction of underwater light fields
Relevance
The quantitative study of underwater light fields in coastal waters and shelf seas has important applications in ecology, engineering and remote sensing. Underwater light fields:
- play an important role in determining rates of photosynthesis by phytoplankton and macrophytes, and therefore set limits on the productivity of marine ecosystems.
- influence the range at which objects are visible under water, which is of great significance for diving and engineering operations and also for visual interactions between predators and prey species.
- determine the volume reflectance of seawater which is important for optical remote sensing.
Dynamics of underwater light fields
Variations in underwater light fields originate from changes in both solar illumination and seawater composition, and predicting this variability involves the study of radiative transfer in an optically complex medium. There is an extensive literature on underwater light fields and associated problems in marine optics, but the fundamental concepts are clearly laid out in the books by Kirk (1994[1]), Mobley (1994[2]) and Bukata et al (1995[3]). One of the challenges posed by coastal light fields is the potential for interaction and between physical and biological factors. For example, sediment particles in suspension can limit the illumination of benthic photosynthetic organisms, but the presence of those organisms may stabilise the sediment surface and reduce the probability of sediment re-suspension taking place.
Underwater light fields are vulnerable to human activities. Anthropogenic disturbances such as eutrophication, dredging operations and accelerated soil erosion due to the de-afforestation of river catchments can modify underwater light climates in coastal regions. Increases in turbidity produced by these activities can damage important ecosystem components such as coral reefs and sea grass beds.
The underwater light field depends on:
- the optical characteristics of sea water: The optical characteristics of coastal waters are determined not only by water itself, but also by suspended particulate material (minerals, organic detritus and phytoplankton) and coloured dissolved organic matter. The presence of relatively high concentrations of dissolved organic matter or minerals often distinguishes coastal waters from those of deeper seas, and accounts for their green or brown colouration.
- the conditions of illumination: The conditions of illumination depend on solar angle, the degree and type of cloud cover, and the state of the sea surface. As a result, underwater light fields show strong diurnal and seasonal variability.
Light field descriptors
Radiance and irradiance
Radiance is the fundamental quantity in light field measurement. It is usually denoted [math]L(q,f,\lambda)[/math] where the angles [math]q[/math] (zenith) and [math]f[/math] (azimuth) specify the direction in which the radiance is measured and [math]\lambda[/math] is the wavelength. The units of radiance are W m-2 nm-1 sr-1. Measurements of the water-leaving radiance [math]L_w[/math] just above the surface at [math]q = 0[/math] (nadir viewing) are particularly important for remote sensing.
Planar and scalar irradiances [math]E_x(\lambda)[/math] are generated by integrating radiances over defined intervals of solid angle [math]D_w[/math]. They have units of W m-2 nm-1. For planar irradiances, the radiances are multiplied by the cosine of their angle of incidence on the detecting plane before carrying out the integration. Scalar irradiances omit the cosine weighting. Measurements of planar irradiances are made using a diffusing disc as a collector, while scalar irradiances are measured use a diffusing sphere. Commonly used irradiances are summarized Table 1.
| Quantity | Name | Angular limits |
|---|---|---|
| [math]E_{\theta}(\lambda)[/math] | Scalar irradiance | whole sphere |
| [math][E_{\theta}(\lambda]_u[/math] | Upward scalar irradiance | lower hemisphere |
| [math][E_{\theta}(\lambda]_d[/math] | Downward scalar irradiance | upper hemisphere |
| [math]E_u(\lambda)[/math] | Upward planar irradiance | lower hemisphere |
| [math]E_d(\lambda)[/math] | Downward planar irradiance | upper hemisphere |
A full description of an underwater light field would involve the specification of the spectral and angular distribution of radiance as a function of depth and geographical location, but this degree of detail is impractically cumbersome. The quantities most frequently specified are upward radiances and upward and downward irradiances.
Wavelength ranges
Studies of underwater light fields are usually contained within a waveband of approximately 300-900 nm: outside these boundaries, absorption by water strongly limits light penetration. Photosynthesis and animal vision mainly utilise the wavelength region of 400-700 nm, but damaging radiation can affect photosynthetic organisms at ultra-violet wavelengths (300-400 nm) while the near infra red region (700-900 nm) is important for remote sensing applications.
Measurement units
Three systems of units may be encountered in the literature on underwater light fields:
- Radiometric units: In physical radiometry, light energy is measured in joules (J), radiometric power in watts (W or J s-1), and the source brightness as power per unit solid angle (W sr-1).
- Quantum units: In photochemistry and photobiology, where molecular events are driven by the absorption of individual quanta, it is often useful to measure light fields in terms of numbers of photons rather than energy. A convenient unit is the mol (Avogadro’s Number) of photons. In the photobiology literature, one mol of photons is often referred to as an einstein, but the unit is redundant. The energy associated with a single photon of a given wavelength in vacuo is [math]e = hc/\lambda[/math], where [math]h[/math] is Planck’s constant and [math]c[/math] the speed of light. The inverse wavelength dependence means that conversion between radiometric and quantum units (for example from W m-2 s-1 to mol photons m-2 s-1 in the case of irradiance) requires explicit knowledge of the spectral distribution of the light field. Integration of scalar quantum irradiance across the visible spectrum (400-700 nm) gives a measure of photosynthetically active radiation (PAR: mol photons m-2 s-1).
- Photometric units: The visual effect of a given source of illumination depends on the spectral sensitivity of the human eye. This leads to a system of photometric units based on the lumen as the measurement of effective power, and is discussed in DeCusatis (1997[4]). Conversion between radiometric and photometric units has to take both the standard eye response curve and the spectral distribution of the light field into account.
Optical properties of natural waters
This section describes the inherent optical properties (IOPs) op natural waters. The total IOP of water is its own contribution and four types of optically significant constituents.
Inherent optical properties (IOPs)
The optical characteristics of a light-transmitting medium can be specified in terms of its inherent optical properties, which represent the effect of an optically thin slab of the medium on the transmission of a collimated light beam. The main IOPs are summarized in table 2:
| [math]a[/math] | absorption coefficient | m-1 |
| [math]b[/math] | scattering coefficient | m-1 |
| [math]c = a + b[/math] | attenuation coefficient | m-1 |
| [math]\beta[/math] | scattering phase function | sr-1 |
Formal definitions for these IOPs may be found in Mobley (1994[2]). The absorption, scattering and attenuation coefficients have fairly obvious meanings, while the phase function is a measure of the relative angular distribution of the scattered light. The scattering coefficient (b) is often partitioned into forward and backwards components, and the backscattering coefficient (bb) is of great importance for determining the remote sensing reflection of a water body.
The total IOPs of a body of seawater can be considered as the sum of the partial contributions from water itself and a number of optically significant constituents. These constituents are generally divided into four classes:
- Phytoplankton cells and colonies (Phyt)
- Mineral suspended solids (MSS)
- Coloured dissolved organic matter (CDOM)
- Organic suspended solids or detritus (OSS)
The concentration of the photosynthetic pigment chlorophyll a (Chl, mg m-3) is often used as a proxy variable for phytoplankton biomass. Mineral particle and organic detritus concentrations (g m-3) are determined by filtering water samples through a fine glass fibre filter and measuring the dry weight of material retained before and after combusting the filter at 500°C to remove the organic portion. Since there is no standard method for measuring the mass concentration of coloured dissolved organic matter, it is conventionally measured as the absorption coefficient at 440 nm of seawater which has been passed through a membrane filter with a 0.2 μm pore size.
The total absorption coefficient can be written as the sum of the contributions of the individual constituents:
[math]a_{total} = a_{water}\, +\, a_{Phyt}\, +\, a_{MSS}\, +\, a_{CDOM}\, +\, a_{OSS} [/math]
The scattering coefficient ([math]b[/math]), attenuation coefficient ([math]c[/math]) and phase function ([math]\beta[/math]) can all be partitioned in a similar manner. In practice, however, the optical contributions of these four classes of material may not be completely distinct: blooms formed by phytoplankton groups such as coccolithophores and diatoms may generate significant concentrations of mineral particles (calcite and silica respectively), and organic detrital material may form flocs which incorporate suspended minerals.
Specific optical properties and characteristics of constituents
The optical contributions of the main classes of constituents can be calculated by multiplying the concentrations of each constituent by the value of its inherent properties expressed per unit concentration. The latter quantity is often referred to as a specific inherent optical property or specific optical cross section. For example:
[math]a_{MSS} = MSS \times a^*(MSS)[/math]
where [math]MSS[/math] is the concentration of suspended minerals and [math]a^*(MSS)[/math] is the specific absorption cross section for this constituent, with units of m2 g-1. The convention that seawater contains four classes of optically significant constituents tends to conceal the fact that there can be considerable variability in specific optical properties within each class of constituent. Moreover, optical characterisation of the four main classes of constituent is currently incomplete.
- Phytoplankton cells and colonies (Phyt): A great deal of effort has been devoted to the study of the absorption and scattering characteristics of phytoplankton cells (see for example Sathyendranath et al 1987[5], Bricaud et al 1988[6] and Johnsen et al 1994[7]). The absorption spectra generally show maxima around the main chlorophyll absorption peaks at 440 nm and 675 nm, with subsidiary features depending on the presence of accessory light harvesting and photoprotective pigments. Phytoplankton scattering poses considerable practical and theoretical challenges because of the wide range of size and structure exhibited by individual cells and colonies. A helpful review of the theoretical problems is given by Quirantes and Bernard (2004[8]) and measurement issues are discussed in Volten et al.(1998[9]). For all but the smallest species, phytoplankton scattering is strongly peaked in the forward direction. One interesting feature in the total scattering spectra is the presence of minima near the chlorophyll absorption peaks which is due to Kettler-Helmholtz anomalous dispersion. There is some evidence that the specific backscattering coefficients of most phytoplankton species are too low to account for the magnitude of water-leaving radiance signals observed from natural populations, but measurements in this area are imprecise and current theoretical models do not take the full structural complexity of phytoplankton cells into account.
- Mineral suspended solids (MSS): The optics of some types of mineral particles have been systematically explored (Babin and Stramski 2005[10]). Their absorption spectra are generally high in the blue wavebands and decrease towards the red, and for field samples their shape is often similar to that for CDOM. Scattering characteristics are influenced by size distribution and refractive index (Wozniak and Stramski 2004[11]). It is not clear whether laboratory samples of mineral dusts are representative of all the materials found in coastal locations.
- Coloured dissolved organic matter (CDOM) CDOM absorption has been extensively characterised. It is generally described by an exponential function of the form: [math]a(\lambda\,)_{cdom}=a(\lambda_{\theta})_{cdom}\, e^{-S(\lambda - \lambda_{\theta})}[/math]. In which: [math]\lambda_{\theta}[/math] is a reference wavelength (usually 440 nm) and [math]S[/math] is a coefficient which has a typical value of 0.01 to 0.02 in UK coastal waters (Bricaud et al 1981[12]). Light scattering by CDOM is generally assumed negligible, but it is possible that some of the coloured material passing through 0.2 μm filters is colloidal in nature and therefore capable of contributing to the total scattering coefficient.
- Organic suspended solids or detritus (OSS): The optical properties of organic detritus are not well characterised. This is due to the wide range of material which falls under this classification, ranging from scenescent phytoplankton cells to faecal pellets in offshore waters and including terrestrial vegetable matter in estuaries. There is also the possibility that organic matter may form flocs which include mineral particles in estuaries and in post-bloom shelf-sea conditions.
Other relevant parameters
Changes in light field parameters with depth ([math]z[/math]) are often approximately exponential in nature. For example, the attenuation of downward planar irradiance in a uniform water column can be written:
[math]E_d(\lambda, z) = E_d (\lambda, \theta)e^{-K_d z}[/math],
in which [math]K_d[/math] is the vertical attenuation coefficient. Quantities such as [math]K_d[/math] are relatively insensitive to input conditions at moderate solar angles and are frequently referred to as apparent optical properties (AOPs) (Kirk 1994[1]). Some examples of AOPs are:
- The attenuation coefficient for downwards planar irradiance ([math]K_d[/math])
- The attenuation coefficient for scalar irradiance ([math]K_{\theta}[/math])
- Irradiance reflectance ([math]R[/math])
- Remote sensing reflectance (measured just above the sea surface) ([math]R_{rs}[/math])
- The mean cosine ([math]\mu[/math])
Photosynthetically available radiation (PAR) is the integral of scalar irradiance, expressed in quantum units, over the 400 -700 nm waveband. The term [math]K_{PAR}[/math], defined by analogy with [math]K_{\theta}[/math] and [math]K_d[/math], is sometimes used to describe the attenuation of PAR. However since the attenuation of light by seawater varies with wavelength, the reduction in PAR with depth can deviate from the exponential approximation in the upper part of the water column. Figure 1 shows the measured variability of PAR with depth for three contrasting stations in the Irish Sea.
The optical depth [math]z(\lambda;l)[/math] is defined as the depth at which [math]E_d[/math] is reduced to 1/e (~0.37) of its value immediately below the surface. This quantity is wavelength-dependent, as might be expected from the fact that the spectral distribution of the underwater light field changes with depth. The maximum depth at which significant photosynthesis can occur (the euphotic depth, [math]z_{eu}[/math]) is conventionally taken to be the point at which PAR is reduced to 1% of its surface value (Kirk 1994[1]).
The horizontal range of visibility ([math]y[/math]) at which a black target is judged to be visible to a human observer is empirically related to the attenuation coefficient [math]c[/math] by the relationship:
- [math]y\, = 4.8 / c [/math] .
A theoretical basis for this relationship, based on radiance transfer theory, is given by Zaneveld and Pegau (2003[13]).
Radiative transfer theory and light field modelling
The radiative transfer equation
The propagation of light energy through a medium which absorbs, scatters and contains internal sources is determined by the radiative transfer equation, which is widely used in fields such as astronomy and atmospheric science as well as hydrological optics (Goody and Yung 1989[14]). In marine light fields, sunlight enters from above and is attenuated with depth ([math]z[/math]). In the simple case where bottom reflectance can be neglected and the water is horizontally homogeneous, the change in monochromatic radiance in a given direction ([math]q,f[/math]) as a function of depth ([math]z[/math]) is given by
[math]\Large\frac{d L(z,q,f)}{dr}\normalsize = -cL(z,q,f) + L^*(z,q,f)+ S(z,q,f)[/math],
in which: [math]L^*(z,q,f)[/math] represents the gain in radiance due to light scattered from adjacent paths and [math]S(z,q,f)[/math] accounts for any internal sources. In coastal waters, the most important internal source terms arise from Raman scattering by water molecules and fluorescence from dissolved organic matter and phytoplankton pigments. For light-field modelling the radiative transfer equation is solved numerically using either Monte Carlo methods or more conceptually sophisticated mathematical techniques (Mobley 1994[2], Thomas and Stamnes 1999[15]). The discrete ordinates method is commonly used in optical oceanography and is implemented in the commercially available Hydrolight software package (Sequoia Scientific). In order to construct a light field model, it is necessary to specify the nature of the input illumination, the IOPs of the medium, and any internal source functions (Figure 2). Light field models can generate a complete set of radiance values, but their output is usually summarised as a set of AOPs and reflectances which corresponds to those most frequently measured.
Optical closure
Ideally, it should be possible to construct a light field model of a coastal water column using measured values of the IOPs which would precisely replicate radiometric measurements made at the same time. This is known as ‘optical closure’. It is difficult to achieve in practice for two main reasons. First, it places great demands on the appropriate calibration and deployment of the measuring instruments. Second, some key IOPs such as the scattering phase function are difficult to measure in situ, and are usually estimated from the backscattering ratio (bb/b) using analytical functions. Figure 3 shows a typical attempt to achieve optical closure for a shelf sea station in the Irish Sea with constituent concentrations of: Chl 1.6 mg m-3, MSS 1.9 mg l-1, CDOM a440 0.2m-1. In this instance the match between measured and modelled [math]E_d[/math] values is reasonably good, but the [math]L_u[/math] plots diverge significantly below 5 m. The symbols in Figure 3 represent measurements made with a profiling radiometer (Satlantic SPMR) and are spaced at 1 m intervals from the sea surface. The lines indicate the output of Hydrolight calculations of downward irradiance (upper plot) and upward radiance (lower plot) which used in-situ measurements of IOPs as inputs. Absorption and scattering coefficients were measured using a dual tube photometer (Wet Labs ac-9) and backscattering coefficients measured using a Hydroscat 2 (HobiLabs) backscattering meter.
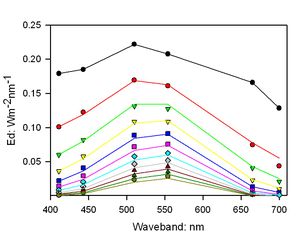
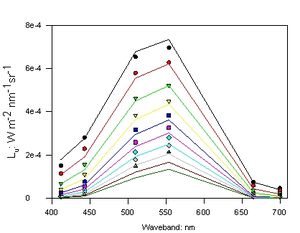
Figure 3: Typical results of an attempt to achieve optical closure for a station in the Irish Sea.
See also
Internal links
- Optical measurements in coastal waters
- Optical remote sensing
- General principles of optical and acoustical instruments
- Optical Laser diffraction instruments (LISST)
- Optical backscatter point sensor (OBS)
- Use of Lidar for coastal habitat mapping
Further reading
- Babin M and Stramski D 2002 Light absorption by aquatic particles in the near-infrared spectral region. Limnology and Oceanography 47:911-915
- Babin, M, Morel A, Fournier-Sicre V, Fell F and Stramski D 2003. Light scattering properties of marine particles in coastal and oceanic waters as related to the particle mass concentration. Limnology and Oceanography, 48, 843-859
References
- ↑ 1.0 1.1 1.2 Kirk J T O 1994 Light and photosynthesis in aquatic ecosystems. Cambridge University Press, Cambridge, 410 pp.
- ↑ 2.0 2.1 2.2 Mobley C D 1994 Light and water; radiative transfer in natural waters. Academic Press, San Diego, 592pp. ISBN 0125027508
- ↑ Bukata R P, Jerome J H , Kondratyev K Y and Pozdnyakov D V 1995 Optical properties and remote sensing of inland and coastal waters. CRC Press, 384pp
- ↑ DeCusatis C M (ed) 1997 Handbook of Applied Photometry. American Institute of Physics Press, New York, 484 pp.
- ↑ Sathyendranath S, Lazzara L, Prieur L 1987 Variations in the Spectral Values of Specific Absorption of Phytoplankton. Limnology and Oceanography 32: 403-415
- ↑ Bricaud, A., Bedhomme, A.L. and A. Morel (1988). Optical properties of diverse phytoplanktonic species: Experimental results and theoretical interpretation, Journal of Plankton Research, 10, 851-873
- ↑ Johnsen G, Samset O, Grauskog L and Sakshaug E 1994 In vivo absorption characteristics in 10 classes of bloom-forming phytoplankton: taxonomic characteristics and responses to photoadaptation by means of discriminant and HPLC analysis. Marine Ecology Progress Series 105:149-157
- ↑ Quirantes A and Bernard S 2004 Light scattering by marine algae: two-layer spherical and nonspherical models. Journal of Quantitative Spectroscopy & Radiative Transfer 89: 311–321
- ↑ Volten H, de Haan J F , Hovenier J W, Scheurs R, Vassen W, Dekker A G, Hoogenboom H J, Charlton F and Wouts R. 1998 Laboratory measurements of angular distributions of light scattered by phytoplankton and silt. Limnology and Oceanography 43: 1180-1197.
- ↑ Babin M., and Stramski D 2005 Variations in the mass-specific absorption coefficient of mineral particles suspended in water. Limnology and Oceanography, 49, 756-767
- ↑ Wozniak, Slawomir B.; Stramski, Dariusz 2004 Modeling the Optical Properties of Mineral Particles Suspended in Seawater and their Influence on Ocean Reflectance and Chlorophyll Estimation from Remote Sensing Algorithms Applied Optics IP, vol. 43, Issue 17, pp.3489-3503
- ↑ Bricaud A, Morel A and Prieur L 1981 Absorption by dissolved organic matter of the sea (yellow substance) in the UV and visible domains. Limnology and Oceanography 26:43-53.
- ↑ Zaneveld J R V and Pegau W S 2003 Robust underwater visibility parameter. Optics Express 11:2997-3009
- ↑ Goody R M and Yung Y L 1989 Atmospheric radiation, theoretical basis. Oxford University Press, Oxford. 519pp.
- ↑ Thomas G E.and Stamnes K 1999 Radiative transfer in the atmosphere and ocean, Cambridge, New York, Cambridge University Press 517 p., ISBN 0521401240.
Please note that others may also have edited the contents of this article.
|

