Modelling coastal hydrodynamics

Introduction

In the analysis of the coastal hydrodynamic processes, modelling (physical, numerical and composite) is often employed to simulate the main phenomena in the coastal region. Physical models (PM) refer to the use of laboratory models at an appropriate scale ( micro, small, medium and large scale models ) for investigating the relevant process, numerical models (NM) refer to the use of computer codes (commercial, open source, home-made software) and composite models (CM) refer to the integrated and balanced use of physical and numerical models. Hydrodynamic modelling forms the basis for many other modelling studies, whether sediment transport, morphology, waves, water quality and/or ecological changes are being investigated. Research is being carried out to improve the representation of tides, waves, currents, and surge in coastal waters.
In the following sections a general outline is given initially with the main characteristics of the coastal hydrodynamics and the associated physical, numerical and composite modelling of the main coastal processes. Phenomena, concepts and insights are presented briefly and modelling of coastal hydrodynamics using physical, numerical and composite models is described. Finally practical applications from the three methodologies are presented together with an extensive list of references.

General outline

Coastal Hydrodynamics and Modelling

Coastal Hydrodynamics

The dynamic processes that exist in the nearshore region are generated by a number of different drivers. Under the influence of these external forces, the fluid motion of the water manifests itself as coastal currents, tides and tidal currents, internal and surface waves, storm surges, tsunamis and others (Horikawa, 1988).
The main difference between coastal waters and deep ocean waters is the presence of two physical constraints (i.e., the sea bottom, at a relatively shallow depth, and the coastline) which somehow determine the motion of the sea water.
The nearshore zone is defined as the region extending from a landward limit associated with storm-wave phenomena (e.g., overwash), to a seaward limit beyond the point where incident waves break, but which depends on the specific context (Horikawa, 1988). Within this zone, several other regions may be distinguished, as shown in figure 1 (Horikawa, 1988). The most relevant of these are the breaker zone, the breaking point, and the surf zone. The former is the zone where incident irregular waves break; the breaking point is where breaking begins and the waves attain maximum height, and the surf zone is defined as the region between the seaward limit of the breaker zone and the area of high turbulence created by the collision of the backrushing water mass and the incoming waves (Horikawa, 1988).

Following Sánchez-Arcilla and Lemos (1990) , the relevant phenomena in the surf zone can be classified into four different types:

1. Sediment transport and corresponding changes in morphology, with a characteristic time scale of 1 day to 1 month, and a spatial scale between 100 m and 1000 m,
2. Currents (non-oscillatory flow), with time scales between 10 minutes and 1 hour, and spatial scales similar to those of sediment transport,
3. Organised oscillatory flows (i.e., wind waves, infra-gravity waves), with time scales ranging from 10^-1 sec to 10 min, and space scales from 1 to 100 m.
4. Random oscillatory flow (turbulence), whose length scales are between 10^-3 to 10¹ sec , and with small (10^-4 to 10^-1 m) spatial scales.

In a general overview, it can be said that the main features in coastal hydrodynamics are the wind waves, generated by the stress exerted on the ocean surface by the wind. As these waves travel from deep waters into shallower regions, they become more non-linear and dissipative, transferring energy from the peak of the spectrum to higher and lower frequencies. Eventually, the proximity of the sea bottom will induce the breaking of the waves, producing a severe increase in the marine turbulence level, and generating different types of currents, which may extend beyond the surf zone.
However, the study of nearshore hydrodynamics is not an easy task. Wave, current and turbulence scales tend to overlap, thus giving rise to the interaction (to some degree) of these three flow types; since the individual flows are non-linear in nature, their interaction becomes quite complex. The usual procedure followed to derive and understand the governing equations is to decompose all the state variables into contributions from currents, waves and turbulence, and then use time-averaging operators to isolate the desired phenomenon.

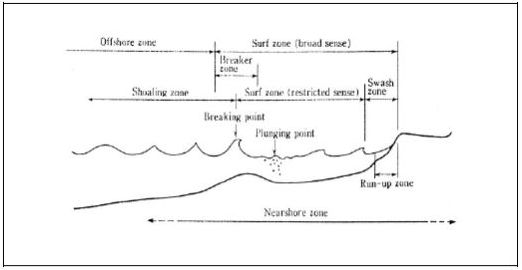
Figure 1: Zone division in the nearshore region (Horikawa 1988)

Physical Modelling

Physical models and laboratory experiments remain part and parcel of the research methodology because of their many strong points, such as:

1. Observability: experiments to investigate mechanisms that are difficult to observe in nature,
2. Measurability: experiments to isolate phenomena that are difficult to measure in nature,
3. Repeatability: repeated experiments, to investigate the range of inherent uncertainty of phenomena,
4. Input control: experiments with various realistic input time series, to assess the predictive capability of numerical models,
5. Process control: experiments for simple situations, in order to validate the results of theoretical behaviour analyses,
6. Overview: experiments concerning spatial pattern formation (wave fields, morphology, etc.) and requiring synoptic measurements,
7. Cost: filling in of field measurements, which are necessarily disperse,
8. Robustness: modelling of processes that cannot be modelled numerically, because (unlike numerical models) physical models are basically similar to prototype (especially in facilities that model processes at full scale).

Facilities of various sizes (from large to micro scale) are available for physical modelling of coastal processes. The size of the facility for use depends on the scale and scope of the phenomenon to be modelled. If the prime interest is in the detail of processes the size of the facility may not be critical but the range of the measuring equipment available may be. If the intention is to model flow-boundary interactions over a large area , a large facility is essential so that model scales of 1:10 or 1:100 can be used. Combining detailed process and scale modelling in different facilities can prove very valuable, nesting the results of process studies of critical zones within those from a less detailed, broader scale model.
Large scale models are desirable since model laws other than Froude scaling (Reynolds, Weber etc) can be considered and the main characteristic parameters can be measured accurately. The scale selection should assure that the dominant forces are well represented. For wave reproduction the capillary forcesshould play an insignificant role only. Consequently, the wave lengths must not be too sort. A practical lower limit is 0.3 m corresponding to a wave period of 0.4 s. Very small scales also affect the repeatability by which the small-scale waves can be reproduced in the laboratory. In tests where viscous effects are important, attention has to be paid to the Reynolds number. This is related primarily to the coastal structure being tested rather than to the ability to reproduce the waves. However, micro-models can be an inexpensive alternative for the hydraulic laboratories of Universities and even medium consultancy firms. They are envisaged as a tool for: the preliminary research of wave-related coastal processes, the development and initial testing of novel ideas, the preliminary design of wave related coastal protection schemes and the testing of alternative design options, the provision of immediate answers and insights to simple coastal engineering problems, the pre-design of large scale physical models.

Physical modelling is more an art than a science when scale and model effects are not taken into account in a physical model . Scale effects are related to the inability to scale all relevant forces from prototype to model scale. Model or laboratory effects are related to the inappropriate set-up of the model and the incorrect reproduction of the governing forces, the boundary conditions, the measurement system and the data analysis. Facilities vary widely and are expensive to install and maintain. The correct facility for the application may not be available.

Numerical Modelling

The rapid development of computing technology has furnished a large number of models to be employed in coastal hydrodynamic problems. A variety of coastal models are available and the modelling techniques have become quite mature . The numerical technique can be based on the finite element method, finite difference method , boundary element method, finite volume method and Eulerian-Lagrangian method. The time-stepping algorithm can be implicit, semi-implicit, explicit, or characteristic-based. The shape function can be of the first order, second order, or a higher order. The modelling can be simplified into different spatial dimensions, i.e., a one-dimensional (1D) model, two-dimensional (2D) depth-integrated model, 2D lateral-integrated model, 2D layered model and 3D model.

An analysis of coastal hydraulics and water quality often demands the application of heuristics and empirical experience, and is accomplished through some simplifications and modelling techniques according to the experience of specialists. However, the accuracy of the prediction is to a great extent dependent on open boundary conditions, model parameters, and the numerical scheme. The adoption of a proper numerical model for a practical coastal problem is a highly specialized task. These predictive tools inevitably involve certain assumptions and/or limitations, and can be applied only by experienced engineers who possess a comprehensive understanding of the problem domain. This leads to severe constraints on the use of models and large gaps in understanding and expectations between the developers and practitioners of a model.

Composite Modelling

Composite Modelling (CM) is defined as the integrated and balanced use of physical and numerical models . Combining physical modelling and numerical modelling, or Composite modelling may open up new opportunities for physical modelling, c.q. lead to a new generation of physical modelling infrastructure.
Several ideas and expectations are associated with CM. Firstly, CM allows to get the best out of both Physical Models (PM) and Numerical Models (NM) for a given problem – apply each for that geographical area or for those scales where it performs best, and so lead to an overall better simulation of the relevant processes. Also it may provide more quality (higher accuracy, reduced uncertainty) against the same cost or it may provide the capabilities to model more complex problems which individual PM or NM cannot.
Several authors have discussed CM, though often with slightly different definitions. Barthel and Funke (1989) referred to it as “hybrid modelling” while Oumeraci (1999) proposes a move towards CM, by combining the main strengths of physical and numerical models within a hydro-informatics style of framework. As part of a CM, physical model tests would be conducted at a large enough scale to minimise the scale effects, and concentrating on important processes that are not well enough understood to be modelled accurately in a numerical model (i.e. interactions of short-scale and long-scale processes). The results are analysed to increase process understanding of the behavior of the system but are also parameterised so that they can be incorporated into a numerical model that covers a wider area. Kamphuis (2000) discusses the use of various types of modelling and the need to provide well-based quantified results in coastal engineering design. He advocates integration of prototype data, physical and numerical modelling as a further element to improve modelling and design. These elements can essentially complement each other – model simulations provide the continuum information to bridge the gaps in field data, etc.

A key element in integrated models is the Computational module (“information manager”) as shown in the following figure.

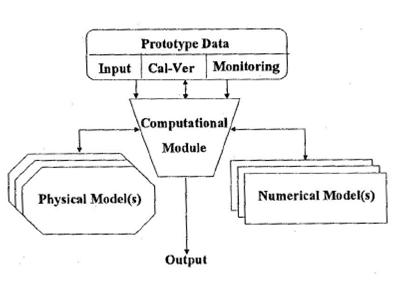
Figure 2: Model integration leading to an integrated model

The integration of numerical modelling systems, field measurements, experimental laboratory research and theoretical analysis, combined through “calculation or integration modules” will lead to what is called “hybrid modelling” or “composite modelling”. For a problem with different spatial scales, modelling the far field by NM, and the near-field with PM, with proper exchange of information between the two, information exchange and results can be tied together computationally. An extensive range of topics have been identified as well as suited for a composite approach in hydraulic modelling
A decision to apply CM is necessarily preceded by a problem analysis, in the form of the question and answers, in order to estimate a priori the potential benefits of using CM.
The state of the art of the tools for analysing the problem needs to be critically determined first. In different words and for obvious reasons somewhat aggregated we can rephrase that in the questions: Which individual approaches and models are available? Which level of sophistications is required / which model or set of models? Are their strengths and weakness such that they can be satisfactorily applied to analyse the problem given the type of answer required?
The answers to these questions will or should give the information whether it makes sense to use CM: Is one type of model not adequate for analysing and solving the problems? Do physical and numerical models complement each other for this problem? Can different scales be separated in time and / or in space? Can the interfacing of the models and the exchange of data be defined uniquely, in terms of quantified parameters? Can an estimate be given of the uncertainty of the transferred data, so the transfer and effect of uncertainties from model to model can be estimated? Oumeraci (1999), Kamphuis (2000) and Van Os et al. (2004) point out the importance of this interfacing, which needs to be quantified, taking into account uncertainties involved. The above provides the material to formulate a hypothesis on what we expect to gain by CM for this problem, for example in terms of: increased cost effectiveness; improved accuracy; reducing uncertainties; tackling problems that could not reasonably be solved by a single model approach; etc. The outcome of this process is an argued decision on whether or not CM is needed, or whether it is beneficial for modelling the problem at hand.

The advantage of approaching this conscientiously lies in the fact that we systematically build up the various elements into, for instance, an exchangeable and easily accessible library of physical and numerical models and their descriptions or metadata. This will provide updates on their capabilities, usefulness, and track records which is part of Good Modelling Practice.

Phenomena and Concepts

The basic theory of the generation of storm surges and waves by wind is understood in principle , although some details still need elucidation. For example, the wind stress is modelled empirically very successfully although the actual process of transfer of momentum and energy from the atmosphere to the sea via wind waves is very complex and not fully understood (Janssen 2004). There are also several interactions between the mean circulation and wind-waves (Peregrine and Jonsson 1983). The propagation of waves in shallow water is dependent on water depth and this means that the total water depth, which includes tide and surge, will affect wave propagation. In fact, the tidal propagation is also modified in the presence of a surge, leading to tide-surge interaction (Wolf 1981) . Waves are modified by the presence of currents generated by tide and surge. They contribute to water level and mean circulation through wave setup and longshore currents, due to radiation stresses in shallow water (Longuet-Higgins and Stewart 1962).

Tides, caused by the gravitational effect of sun and moon, are periodic and very predictable. Surges, on the other hand, are quasi-periodic and caused by meteorological forcing. The most important mechanism for surge generation is wind-stress acting over shallow water. Surges at the coast are produced by Ekman dynamics, behaving as forced Kelvin waves . The size of the surge is proportional to the wind-stress divided by the water depth. The wind-stress is usually taken to be proportional to the square of the wind-speed with a drag coefficient which increases with wind speed accounting for some effect of surface roughness due to waves .

Due to transient effects there is also an increase in surge height with wind duration. Surges are, therefore, largest where storms impact on large areas of shallow continental shelves. In deep water, surge elevations are approximately hydrostatic with a 1 hPa decrease in atmospheric pressure giving about 1 cm increase in surge elevation . Surges in the Mediterranean as a whole are likely to be much lower due to the much deeper water. However, they are important in local areas of shallow water, e.g. the Northern Adriatic, where Venice is susceptible to flooding. Some modification is caused by seiching, when winds trigger oscillations at the natural periods of enclosed sea areas, e.g. in the Adriatic the wind tends to trigger the 22-h seiche and its harmonics (11 and 7-h oscillations).
It has long been recognized that in shallow water areas with a large tidal range, the nonlinear effects of tide–surge interaction are important. The peak of the surge in the southern North Sea tends to ‘avoid’ predicted tidal high water, due to the speeding up of the tidal wave propagation in the presence of the deeper water caused by the surge level and other subtle changes are caused by bottom friction. Jones and Davies (1998) and Horsburgh and Wilson (2007), among others, have described work on the effects of tide–surge interaction.
Figure 3 illustrates the mechanism by which tide-surge interaction leads to a surge peak on the rising tide. The tidal phase is advanced due to the deeper water caused by the presence of a positive surge level. The difference between the phase-shifted (T0) and undisturbed tide (T) is added to the surge to give the net tidal residual (red line), which has a peak 3 h before predicted high water.

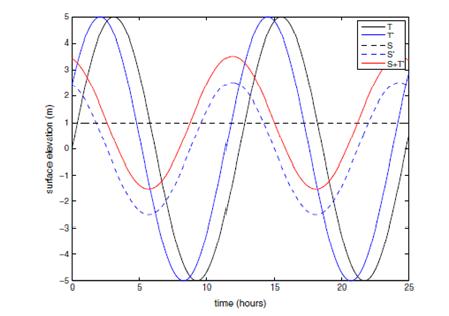
Figure 3: Illustration of tide-surge interaction. Undisturbed tide (predicted tide, T) is solid black line, phase advanced tide (T’) is solid blue line, meteorological surge (S) is dashed black line, tide-surge interaction (S’) is dashed blue line, net residual is solid red line ( Wolf, 2009)

There are several mechanisms by which waves and the currents and water level associated with tide and surge interact, each component of the combined motion affecting the others .
These may be summarized as:

1. the effects of water levels and currents on waves and
2. the effect of waves on tides and surges.

First, the effect of water levels on nearshore wave transformation are considered. As waves enter shallow water, when the depth is less than half the wavelength, the processes of shoaling and refraction change the wavelength and phase speed but the wave period remains constant (in the absence of currents). As energy propagates at the group velocity, by energy conservation the wave height first decreases then increases (this is because of the group velocity property that it increases first with intermediate depth, only to decrease when the depth becomes shallower .
Finally, the energy dissipation processes of breaking and bottom friction start to limit the wave height. If the water depth is modified, by mean sea level changes or tide and/or surge, this will have corresponding effects on wave height. At the coast an increase in water depth will increase the wave height and also the distance to which waves can penetrate inland. Tide and surge currents can affect wave generation, propagation and dissipation. The effect on surface stress is to change the apparent wind and effective fetch. There may also be an enhancement of the wave friction in the bottom stress although Soulsby and Clarke (2005) state this is negligible. Current gradients in the horizontal also cause wave refraction and currents produce a Doppler shift of frequency. In the presence of currents it is the wave action which is conserved rather than wave energy. All these processes are described in more detail in Wolf et al. (1988), Osuna and Wolf (2005) and Ozer et al. (2000) .
Waves can affect the mean flow and water level in the nearshore zone through radiation stress causing longshore drift and wave setup (Longuet-Higgins and Stewart 1962). In the surface layer there is a net transport due to waves (Stokes’ drift). Waves may affect the generation of surges by affecting surface roughness. Janssen (1989, 1991) introduced the concept of wave stress in which wave age affects the surface roughness and implemented it in the WAM model. Further investigation of this has been carried out by Brown and Wolf (2009) . Waves may enhance the bottom friction experienced by currents in shallow water .

Physical, Numerical and Composite Modelling

Physical Models

Wind, waves and swell can be reproduced satisfactorily by a physical model which has to be chosen dependent on various project and site specific parameters like

1. model test objectives
2. proposed structure design and rationale behind the proposed structure. These include typical cross sections, detailed drwings of the structure and material related information such as density of material and grain size information
3. bathymetric details of the surrounding area (3D) or the wave approach direction (2D) so that a representative bottom configuration can be constructed. Good quality bathymetric data will assure that wave transformation is well simulated in the model
4. environmental design conditions (wave height, period, water level, wave spectra and wave direction)
5. structure performance criteria such as allowable damage level, maximum wave run-up, permissible wave transmission at design wave and water level conditions.

The use of physical models for understanding the impact of water waves is essential for the design of marine structures and assessment of coastal development due to natural causes as well as human intervention. For physical model tests wave characteristics have to be selected like

1. the types of the waves to be used (regular, irregular, multi-directional, etc). The selection of wave conditions in the model must be carefully considered in relation to the actual problem.
2. the model scale ratios. The largest possible scale for the available experimental facility is generally selected. Other limitations than physical dimensions may play an important role in scale ratio selection (wavemaker capacity, towing speed etc).
3. representative sea states. Wave characteristics from the actual project location shall be the basis for selection of representative sea states for a model test programme. The selection also depends on the application.
4. the duration of the time series. In some cases very long testing time is required to obtain enough information to derive design values.
5. Free and bound long waves. Any structure or coastline is highly reflective when exposed to long waves. While long waves can often escape to deep water under natural conditions, they are inevitably entrapped in traditional laboratory experiments. Active absorption systems can assist the transparency of offshore boundaries to long waves. Although solved in practice, there are serious practical problems in handling long waves by the wave generator. In shallow water the necessary stroke of the wave generator is very large and may therefore restrict reproduction off extreme sea states at a satisfactory model scale.
6. 2D/3D waves. Selection of 2D or 3D wave testing depends on the problem to be investigated, however, a general experience shows that 2D testing is sufficient for a large range of problems. The general lack of good quality directional wave data is also used as a reason not to use 3D testing. In 3D wave basins the treatment of boundary effects such as wave reflection or damping at the boundaries of the wave basin requires larger efforts than in 2D modelling. Monitoring of 3D wave field within the basin can also be problematic. In 3D basins the wave conditions are more inhomogeneous in space than in 2D flumes. Hence, wave conditions in the 3D basins require higher resolution monitoring of wave parameters.

   The planning and execution of tests and the measurement and the analysis of laboratory waves are essential parts of physical modelling.

Numerical Models

Storm surges are modeled in detail for a variety of reasons, including most, if not all, of the preceding components for real shorelines as a function of time. One possible reason is the prediction of the 50- or 100-year storm surge at a coastal site for the design water levels for coastal structures or the establishment of hazards and insurance rates for coastal communities. Another purpose, involving real-time modeling, is for hazard mitigation and public safety. Alternatively, the hind casting of a given historical storm surge may be carried out to determine the nature and extent of the surge or to calibrate and verify a “new” surge model. The last problem is far easier than the first two, for often data concerning the storm parameters and the wind fields can be obtained. Owing to the lack of long-term water level records or any records at all, statistical surge information is usually unavailable. For actual surge occurrences, often not much data are available except from a few established tide gauge sites and site-specific evidence such as high water levels inside buildings, elevation of wave damage, and other indicators of storm water level.

For any surge model, an adequate representation of a wind field is necessary because the spatial extent of the wind and pressure fields associated with a storm is needed as input. Further, the path of the storm and its correct forward speed are necessary.

Barotropic tides and surges are generally modelled using the ‘shallow-water equations’ since they have very long wavelengths (hundreds of kilometers) compared to the water depth . Heaps (1983) , Flather (1981) and Pugh (1987) reviewed earlier work on numerical modelling of storm surges. Limited area models are subject to errors in boundary conditions and tidal models may omit some tidal frequencies, local effects of the tide generating forces and load tide response of the solid Earth. Shum et al.(1997) reviewed ocean tidal models, concluding that all the models agree within 2–3 cm in the deep ocean.

However, tidal models are still inferior to harmonic analysis and prediction for shallow water tides at locations where coastal tide gauge data are available. The tide–surge model predictions reflect this in using the model surge together with harmonic predictions for tides to provide the total water level .
A surge model inter comparison exercise (de Vries et al. 1995), using common bathymetry and wind forcing, showed only small differences between models, but highlighted the need for accurate wind-stress since there was a tendency for all models to underestimate the surge. Work on the UK tide–surge model by Williams and Flather (2000) has also shown a need for enhanced wind-stress relative to Smith and Banke (1975) and recently Brown and Wolf (2009) have shown this may be related to wave effects and also nearshore bathymetric resolution.
Numerical wave models can be distinguished into two main categories: phase-resolving models, which are based on vertically integrated, time-dependent mass and momentum balance equations, and phase-averaged models, which are based on a spectral energy balance equation. The application of phase-resolving models, which require 10 ~ 100 time steps for each wave period, is still limited to relatively small areas, O (1 ~ 10 km), while phase averaged models are more relax in the spatial resolution and can be used in much larger regions. Moreover, none of the existing models, phase-resolving or not, considers all physical processes involved.
The more recent research efforts have been focused on the development of unified phase-resolving models, which can describe transient fully nonlinear wave propagation from deep water to shallow water over a large area. In the mean time, significant progress has also been made in simulating the wave-breaking process by solving the Reynolds Averaged Navier Stokes (RANS) equations with a turbulence closure model. These RANS models have also been employed in the studies of wave and structure interactions.
Continuing efforts have been made to construct a unified model that can propagate wave from deep water into shallow water, even into the surf zone. The forerunner of this kind of effort is the ray approximation for infinitesimal waves propagating over bathymetry that varies slowly over horizontal distances much longer than local wavelength. In this approximation, one first finds wave rays by adopting the geometrical optic theory, which defines the wave ray as a curve tangential to the wave number vector. One then calculates the spatial variation of the wave envelope along the rays by invoking the principle of conservation of energy. Numerical discretization can be done in steps along a ray not necessarily small in comparison with a typical wave length. Since the ray approximation does not allow wave energy flux across a wave ray, it fails near the caustics or the focal regions, where neighboring wave rays intersect, diffract and possibly nonlinearity are important. While ad hoc numerical methods for local remedies are available, it is not always convenient to implement them in practice.
Within the framework of linear wave theory, an improvement to the ray approximation was first suggested by Eckart (1952) and was later rederived by Berkhoff , who proposed a two-dimensional theory that can deal with large regions of refraction and diffraction. The underlying assumption of the theory is that evanescent modes are not important for waves propagating over a slowly varying bathymetry, except in the immediate vicinity of a three-dimensional obstacle.
The mild-slope equation in modeling wave propagation from deep water to shallow water is successful, because the vertical profile of the velocity is prescribed “correctly” according to the linear wave theory. The mild-slope equation can be applied to a wave system with multiple wave components as long as the system is linear and these components do not interact with each other. In applying the mild-slope equation to a large region in coastal zone, one encounters the difficulty of specifying boundary conditions along the shoreline, which are essential for solving the elliptic- type mild-slope equation. The difficulty arises because the location of the breaker cannot be determined a priori. A remedy to this problem is to apply the parabolic approximation to the mild-slope equation . For essentially forward propagation problems, the so called parabolic approximation expands the validity of the ray theory by allowing wave energy “diffuse” across the wave “ray”. Therefore, the effects of diffraction have been approximately included in the parabolic approximation.

References

The main author of this article is Prinos, Panayotis Please note that others may also have edited the contents of this article. Citation: Prinos, Panayotis (2012): Modelling coastal hydrodynamics. Available from http://www.coastalwiki.org/wiki/Modelling_coastal_hydrodynamics [accessed on 25-11-2024] For other articles by this author see Category:Articles by Prinos, Panayotis