Difference between revisions of "Behaviour-based models"
Tasomerville (talk | contribs) m |
|||
| Line 1: | Line 1: | ||
=== General description === | === General description === | ||
A Behaviour-based model may be defined as a phenomenological model where some of the processes involved in the evolution may have been simplified using semi-empirical averaged formulae (de Vriend 1993<ref> De Vriend, H. J., M. Campobianco, T. Chesher, H. E. de Swart, B. Latteux and M. J. F. Stive (1993). ‘Approaches to long-term modelling of coastal morphology: a review’, Coastal Engineering 21, 225-269.</ref>, Niedoroda et al. 1995<ref>Niedoroda A. W., Reed C. W., Swift D. J. P., Arato H., Hoyanagi K., 1995, ‘Modeling shore-normal large-scale coastal evolution’ , Marine Geology 126 (1-4), 181-199.</ref>). There is no clear boundary between process-based models, described in the previous section, and behaviour-based models, except for the fact that in process-based models the hydrodynamics and transport processes are clearly integrated in the model (to the best knowledge or for the purposes of the modeller), and that the parameters are assumed to be constant or some simple function of space and time (in most cases they are assumed as constant, for simplicity). However, when many details are involved, the computations are very difficult to achieve. Also, process-based models are good at describing the dynamics at short time scales, but mechanisms relevant at short time scales may not dominate at longer scales, and in such cases behaviour-based models tend to lead give better predictions. Therefore, behaviour-based models are advantageous both from a practical and a scientific perspective. | A Behaviour-based model may be defined as a phenomenological model where some of the processes involved in the evolution may have been simplified using semi-empirical averaged formulae (de Vriend 1993<ref> De Vriend, H. J., M. Campobianco, T. Chesher, H. E. de Swart, B. Latteux and M. J. F. Stive (1993). ‘Approaches to long-term modelling of coastal morphology: a review’, Coastal Engineering 21, 225-269.</ref>, Niedoroda et al. 1995<ref>Niedoroda A. W., Reed C. W., Swift D. J. P., Arato H., Hoyanagi K., 1995, ‘Modeling shore-normal large-scale coastal evolution’ , Marine Geology 126 (1-4), 181-199.</ref>). There is no clear boundary between process-based models, described in the previous section, and behaviour-based models, except for the fact that in process-based models the hydrodynamics and transport processes are clearly integrated in the model (to the best knowledge or for the purposes of the modeller), and that the parameters are assumed to be constant or some simple function of space and time (in most cases they are assumed as constant, for simplicity). However, when many details are involved, the computations are very difficult to achieve. Also, process-based models are good at describing the dynamics at short time scales, but mechanisms relevant at short time scales may not dominate at longer scales, and in such cases behaviour-based models tend to lead give better predictions. Therefore, behaviour-based models are advantageous both from a practical and a scientific perspective. | ||
| − | A behaviour-based model formulation is schematised in Figure 4, showing the different steps involved when modelling using a simplified approach. A similar schematic could describe a process-based model, except for the filter of the boundary conditions and the parameter estimations. Indeed, the model may initially use bathymetry inputs from observations, or an explicit form of the bathymetry as predicted from a process-based model. The bathymetry is then updated, and compared to available data. If the prediction is not accurate enough, the model parameters are adjusted. Also, assumptions are made on the most important physical processes and how affect the evolution the system under study. For instance, in 1-line and N-line models in general (see article by A. Falques for more details), it is assumed that the shoreline or underwater lines are in equilibrium, and that diffusion is the dominant process. In such a model the diffusion coefficient is adjusted until the model reproduces the behaviour to a required accuracy. Many behaviour-based models are numerical in nature, due to the complexity of measured boundary conditions. A few examples are given in the next section. | + | A behaviour-based model formulation is schematised in Figure 4, showing the different steps involved when modelling using a simplified approach. A similar schematic could describe a process-based model, except for the filter of the boundary conditions and the parameter estimations. Indeed, the model may initially use [[bathymetry]] inputs from observations, or an explicit form of the [[bathymetry]] as predicted from a process-based model. The [[bathymetry]] is then updated, and compared to available data. If the prediction is not accurate enough, the model parameters are adjusted. Also, assumptions are made on the most important physical processes and how affect the evolution the system under study. For instance, in 1-line and N-line models in general (see article by A. Falques for more details), it is assumed that the shoreline or underwater lines are in equilibrium, and that diffusion is the dominant process. In such a model the diffusion coefficient is adjusted until the model reproduces the behaviour to a required accuracy. Many behaviour-based models are numerical in nature, due to the complexity of measured boundary conditions. A few examples are given in the next section. |
[[Image:ModelsFigure4.png|centre|frame|Figure 4: Schematic showing the steps involved in behaviour-based modelling for long-term studies of bathymetric evolution.]] | [[Image:ModelsFigure4.png|centre|frame|Figure 4: Schematic showing the steps involved in behaviour-based modelling for long-term studies of bathymetric evolution.]] | ||
| Line 13: | Line 13: | ||
| − | Niedoroda et al. (1995) and Stive and de Vriend (1995) <ref>Stive M. J. F. and de Vriend H. J., 1995, ’Modeling shoreface profile evolution’, Marine Geology 126 (1-4), 235-248.</ref> have applied behavioural concepts to analyse cross-shore bathymetric evolution at lengthscales of kilometres and timescales of years to decades. In Niedoroda et al. (1995) the sediment fluxes are represented by generalized functions that describe the dynamics. The models assume that longshore gradients are at least two orders of magnitude smaller than cross-shore gradients, and thus longshore gradients can be neglected. The sediment source is shorewards. In the case of Niedoroda et al. (1995) the shelf is assumed to be composed of sediment so the profile shape is unrestrained, and the sediment is assumed to be of the same size in all the morphodynamic features. Given the length and timescales of interest, the hydrodynamics are generalized as large-scale turbulence as in Clarke et al. (1983) <ref>ClarkeT. L., Swift D. I. P., Young R. A., 1983, ‘A stochastic modelling approach to the fine sediment budget of the New-York Bight’, Journal of Geophysical Research-Oceans and Atmospheres 88 (14), 9653-9660. </ref> (as cited by Niedoroda et al., 1995), and advection is assumed to be small. The sediment transport is taken as the sum of a gravity-driven term to account for downslope forces, a net bedload term to acknowledge onshore transport that opposed the effects of gravity, and a diffusion term to account for suspended load. The need for an advective term is recognized when the bottom shelf velocity is important but it is not clear how this velocity was determined for such cases. The authors suggest that applying Bruun’s rule (1962)<ref> Bruun, P., 1962, ‘Sea level rise as a cause of shore erosion’, J. Waterways Harbors Div., ASCE 88, 117-130.</ref> is inaccurate because their simulations show profile changes with time as a consequence of sea level, with fast changes in the nearshore region and slower changes offshore. Their simulations also seem to agree with the observations of sandbar formation nearshore and sandbar travelling in the offshore direction during moderate conditions, when diffusion processes are more important (Ruessink and Kroon, 1994). Also, when considering single grain sizes profile response times agree well with those predicted by Stive and De Vriend (1995), as the authors indicate. However, as noted by Stive and de Vriend (1995), due to the empirical assumptions in behaviour-based models the conclusions tend to be case-dependent and not easily generalised. | + | Niedoroda et al. (1995) and Stive and de Vriend (1995) <ref>Stive M. J. F. and de Vriend H. J., 1995, ’Modeling shoreface profile evolution’, Marine Geology 126 (1-4), 235-248.</ref> have applied behavioural concepts to analyse cross-shore bathymetric evolution at lengthscales of kilometres and timescales of years to decades. In Niedoroda et al. (1995) the sediment fluxes are represented by generalized functions that describe the dynamics. The models assume that longshore gradients are at least two orders of magnitude smaller than cross-shore gradients, and thus longshore gradients can be neglected. The sediment source is shorewards. In the case of Niedoroda et al. (1995) the shelf is assumed to be composed of sediment so the profile shape is unrestrained, and the sediment is assumed to be of the same size in all the morphodynamic features. Given the length and timescales of interest, the hydrodynamics are generalized as large-scale turbulence as in Clarke et al. (1983) <ref>ClarkeT. L., Swift D. I. P., Young R. A., 1983, ‘A stochastic modelling approach to the fine sediment budget of the New-York Bight’, Journal of Geophysical Research-Oceans and Atmospheres 88 (14), 9653-9660. </ref> (as cited by Niedoroda et al., 1995), and advection is assumed to be small. The sediment transport is taken as the sum of a gravity-driven term to account for downslope forces, a net [[bedload]] term to acknowledge onshore transport that opposed the effects of gravity, and a diffusion term to account for suspended load. The need for an advective term is recognized when the bottom shelf velocity is important but it is not clear how this velocity was determined for such cases. The authors suggest that applying Bruun’s rule (1962)<ref> Bruun, P., 1962, ‘Sea level rise as a cause of shore erosion’, J. Waterways Harbors Div., ASCE 88, 117-130.</ref> is inaccurate because their simulations show profile changes with time as a consequence of sea level, with fast changes in the [[nearshore]] region and slower changes offshore. Their simulations also seem to agree with the observations of sandbar formation [[nearshore]] and sandbar travelling in the offshore direction during moderate conditions, when diffusion processes are more important (Ruessink and Kroon, 1994). Also, when considering single grain sizes profile response times agree well with those predicted by Stive and De Vriend (1995), as the authors indicate. However, as noted by Stive and de Vriend (1995), due to the empirical assumptions in behaviour-based models the conclusions tend to be case-dependent and not easily generalised. |
=== References === | === References === | ||
Revision as of 10:37, 17 September 2008
General description
A Behaviour-based model may be defined as a phenomenological model where some of the processes involved in the evolution may have been simplified using semi-empirical averaged formulae (de Vriend 1993[1], Niedoroda et al. 1995[2]). There is no clear boundary between process-based models, described in the previous section, and behaviour-based models, except for the fact that in process-based models the hydrodynamics and transport processes are clearly integrated in the model (to the best knowledge or for the purposes of the modeller), and that the parameters are assumed to be constant or some simple function of space and time (in most cases they are assumed as constant, for simplicity). However, when many details are involved, the computations are very difficult to achieve. Also, process-based models are good at describing the dynamics at short time scales, but mechanisms relevant at short time scales may not dominate at longer scales, and in such cases behaviour-based models tend to lead give better predictions. Therefore, behaviour-based models are advantageous both from a practical and a scientific perspective. A behaviour-based model formulation is schematised in Figure 4, showing the different steps involved when modelling using a simplified approach. A similar schematic could describe a process-based model, except for the filter of the boundary conditions and the parameter estimations. Indeed, the model may initially use bathymetry inputs from observations, or an explicit form of the bathymetry as predicted from a process-based model. The bathymetry is then updated, and compared to available data. If the prediction is not accurate enough, the model parameters are adjusted. Also, assumptions are made on the most important physical processes and how affect the evolution the system under study. For instance, in 1-line and N-line models in general (see article by A. Falques for more details), it is assumed that the shoreline or underwater lines are in equilibrium, and that diffusion is the dominant process. In such a model the diffusion coefficient is adjusted until the model reproduces the behaviour to a required accuracy. Many behaviour-based models are numerical in nature, due to the complexity of measured boundary conditions. A few examples are given in the next section.
Examples
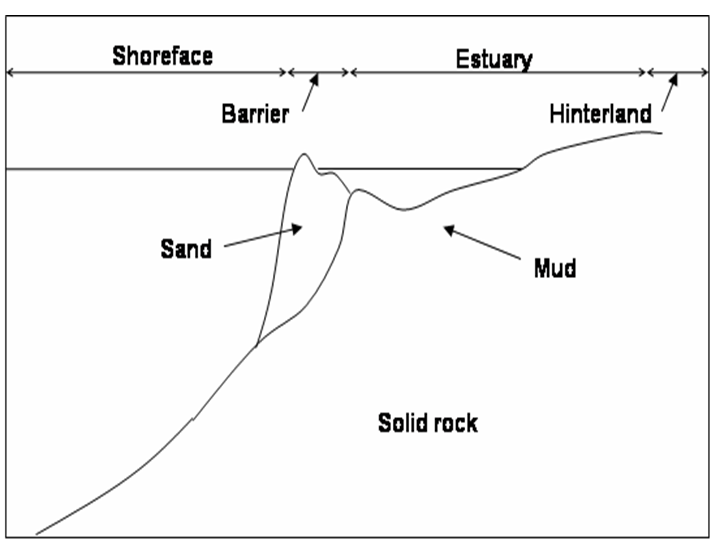
Behaviour-based models have been widely used in long-term coastal morphodynamics, due to the difficulty in assessing which processes are of relevance in decadal time scales. Most of these model use simplifications or heuristic estimates of some sort, be it in the parameter estimation or in the initial boundary conditions, and rely heavily on numerical computations. The Shoreface translation model (STM) developed by Cowell et al. (1992[3],1995[4]) is one of such models, where predictions are made using parameter estimates and initial bathymetric profiles based on data. The model assesses time and space evolution of the beach and bathymetric profile based on sediment budgets, sediment substrate composition, and sea level rise (see section 6.2 for a stochastic extension of this model for forecast applications). Another behaviour-based model recently developed is that by Stolper et al. (2005),[5] to analyse morphological long-term evolution due to sea level rise and sediment exchanges between the shoreface, a barrier, and an estuary. The conservation equations between Stolper et al. (2005) and Cowell et al. (1995) [6] are of the same form, but Stolper et al. (2005) consider different stratigrafic components characterised not only by their subtrate composition, but also by their erodibility. A schematic of some of the morphological components shoreface models may include is shown in Figure 5. Also, while Cowell et al. (1995) [7] are interested in shoreface evolution for times in the order of decades, Stolper et al. (2005) study shoreface evolution occurring in millenia. This shows the vast time range for which a behaviour-based model may be applicable, in contrast to process-based models which are valid only in the short to medium term.
Niedoroda et al. (1995) and Stive and de Vriend (1995) [9] have applied behavioural concepts to analyse cross-shore bathymetric evolution at lengthscales of kilometres and timescales of years to decades. In Niedoroda et al. (1995) the sediment fluxes are represented by generalized functions that describe the dynamics. The models assume that longshore gradients are at least two orders of magnitude smaller than cross-shore gradients, and thus longshore gradients can be neglected. The sediment source is shorewards. In the case of Niedoroda et al. (1995) the shelf is assumed to be composed of sediment so the profile shape is unrestrained, and the sediment is assumed to be of the same size in all the morphodynamic features. Given the length and timescales of interest, the hydrodynamics are generalized as large-scale turbulence as in Clarke et al. (1983) [10] (as cited by Niedoroda et al., 1995), and advection is assumed to be small. The sediment transport is taken as the sum of a gravity-driven term to account for downslope forces, a net bedload term to acknowledge onshore transport that opposed the effects of gravity, and a diffusion term to account for suspended load. The need for an advective term is recognized when the bottom shelf velocity is important but it is not clear how this velocity was determined for such cases. The authors suggest that applying Bruun’s rule (1962)[11] is inaccurate because their simulations show profile changes with time as a consequence of sea level, with fast changes in the nearshore region and slower changes offshore. Their simulations also seem to agree with the observations of sandbar formation nearshore and sandbar travelling in the offshore direction during moderate conditions, when diffusion processes are more important (Ruessink and Kroon, 1994). Also, when considering single grain sizes profile response times agree well with those predicted by Stive and De Vriend (1995), as the authors indicate. However, as noted by Stive and de Vriend (1995), due to the empirical assumptions in behaviour-based models the conclusions tend to be case-dependent and not easily generalised.
References
- ↑ De Vriend, H. J., M. Campobianco, T. Chesher, H. E. de Swart, B. Latteux and M. J. F. Stive (1993). ‘Approaches to long-term modelling of coastal morphology: a review’, Coastal Engineering 21, 225-269.
- ↑ Niedoroda A. W., Reed C. W., Swift D. J. P., Arato H., Hoyanagi K., 1995, ‘Modeling shore-normal large-scale coastal evolution’ , Marine Geology 126 (1-4), 181-199.
- ↑ Cowell, P. J, Roy, P. S. and Jones, R. A., 1992, ‘Shoreface translation model: computer simulation of coastal-sand-body response to sea level rise’, Mathematics and Computers in Simulation 33, 603-608.
- ↑ Cowell, P. J, Roy, P. S. and Jones, R. A., 1995, ‘Simulation of large-scale coastal change using a morphological behaviour model’, Marine Geology 126 (1-4), 45-61.
- ↑ Stolper, D., List, J. H. and Thieler E. R., 2005, ‘Simulating the evolution of coastal morphology and stratigraphy with a new morphological-behaviour model (GEOMBEST)’, Marine Geology 218 (1-4), 17-36
- ↑ Cowell, P. J, Roy, P. S. and Jones, R. A., 1995, ‘Simulation of large-scale coastal change using a morphological behaviour model’, Marine Geology 126 (1-4), 45-61.
- ↑ Cowell, P. J, Roy, P. S. and Jones, R. A., 1995, ‘Simulation of large-scale coastal change using a morphological behaviour model’, Marine Geology 126 (1-4), 45-61.
- ↑ Cowell, P. J, Roy, P. S. and Jones, R. A., 1995, ‘Simulation of large-scale coastal change using a morphological behaviour model’, Marine Geology 126 (1-4), 45-61.
- ↑ Stive M. J. F. and de Vriend H. J., 1995, ’Modeling shoreface profile evolution’, Marine Geology 126 (1-4), 235-248.
- ↑ ClarkeT. L., Swift D. I. P., Young R. A., 1983, ‘A stochastic modelling approach to the fine sediment budget of the New-York Bight’, Journal of Geophysical Research-Oceans and Atmospheres 88 (14), 9653-9660.
- ↑ Bruun, P., 1962, ‘Sea level rise as a cause of shore erosion’, J. Waterways Harbors Div., ASCE 88, 117-130.
Please note that others may also have edited the contents of this article.
|
