Difference between revisions of "Currents and turbulence by acoustic methods"
| Line 47: | Line 47: | ||
<math>u=\frac{u_3-u_4}{2sin\theta}; \quad \quad v=\frac{u_1-u_2}{2sin\theta}; \quad\quad w=\frac{u_1+u_2}{2cos\theta}=\frac{u_3+u_4}{2cos\theta}</math> | <math>u=\frac{u_3-u_4}{2sin\theta}; \quad \quad v=\frac{u_1-u_2}{2sin\theta}; \quad\quad w=\frac{u_1+u_2}{2cos\theta}=\frac{u_3+u_4}{2cos\theta}</math> | ||
| + | |||
| + | == The variance method to calculate Reynolds stresses, turbulence production, eddy viscosity and drag coefficients == | ||
| + | |||
| + | Separating the velocities into mean and fluctuating quantities and taking the difference between the two opposing beams it can be shown by combining the the equation and ensemble average them that: | ||
| + | |||
| + | <math><{u\prime w\prime}>=\frac{{<u\prime_3^2>}-{<u\prime _4^2>}}{4sin\theta cos\theta} | ||
Revision as of 16:24, 23 July 2007
Contents
Introduction
Acoustic Doppler current meters (Velocimeters & Profilers) are used to measure currents in the ocean; the original idea as its name stands is to use the Doppler shift to calculate velocity. The Doppler shift is the observed change of sound pitch as result from relative motion. An example of Doppler effect is the sound made by a vehicle approaches, i.e. a car has a higher pitch as it approaches and lower as it goes away. This change in pitch is proportional to how fast the vehicle is moving (this the same technique used by speed cameras and speed guns used by police). So if we can measure how much the pitch changes we can measure how fast the vehicle goes.
The speed of sound is:
[math]C=F\times\lambda[/math]
The Doppler shift is the difference between the frequency when there is no movement and the difference when either the target or the source or both are moving and is:
[math]F_D = F{C \over V}[/math]
where F the sound frequency, λ is the sound wave length , FD is the Doppler Shift, and V is the is the relative velocity between source and receiver.
In the case of all the acoustic Doppler profilers and current meters (but not velocimeters) the transducer works as both a transmitter and a receiver, so that the equation changes to:
[math]F_D = 2F{C \over V}[/math]
So if we know the original frequency and velocity of sound we can measure the frequency change and infer the along sound (beam) velocity. Because we can only measure the along beam velocity instruments have 3 or 4 transducers, so that the 3 velocity components can be measured. The problem of this technique is that each along beam velocity is going to be measuring a different part of the water so we have to assume that the velocity movement is the same within that area.
All comercial Doppler profilers and current meters (not the velocimeters) are capable to use this technique (Narrow Band). This are the most popular instruments available:Teledyne RD InstrumentsSonTekNortekAanderaa
Broadband and coherent techniques
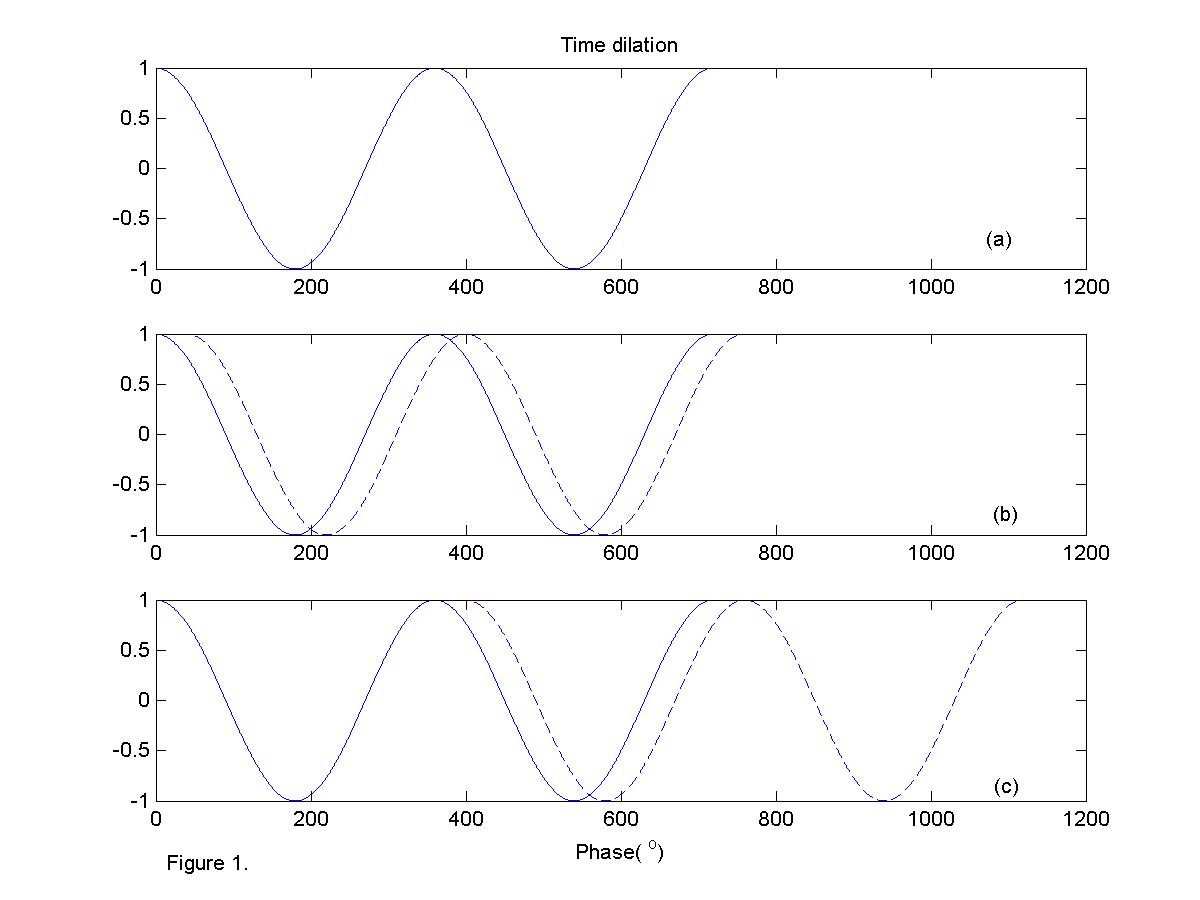
Until now we have been working with the Doppler effect in terms of frequency, but to understand how Broadband (patented by RDI) and the phase coherent techniques we have to discuss the signal changes in the time domain, this is termed time dilation.
If we send a pulse of sound to a stationary particle, the echo from this pulse of sound will result the same (Figure 1a). If the particle moves away from the transmitter it will take longer to the sound to go back and forth (Figure 1b). This change in travel time cause by the distance travelled is called propagation delay.
Echoes from a particle always look the same when the particle does not move, i.e. there is no propagation delay. Echoes have the same relative phase which means zero phase change. In the case of superimposing a second echo on a particle moving away from the transducer, we have that the second echo would be delayed with respect of the first one. I the case of the example shown in figure 1a, the delayed echo shown as a dashed line, has a phase delay of 40o. A propagation delay corresponds to a change in distance, so if we measure the delay and we know the speed of sound we can estimate how much the particle has moved and because we know the time lag between pulses we can calculate the particle velocities.
The main problem of measuring the phase is that phase can only be measured between 0 and 360o, once it reaches 360o it starts again at 0o, so in the case of the example in figure 1, a change of 40o or a change of 400o would be the same, this is called phase ambiguity. To solve this problem we need to figure out how many times the phase has passed through 360o, this is called ambiguity resolution.
Broadband and pulse coherent use the autocorrelation method to process complicated real-world echoes to obtain velocity. In pulse coherent processing, two pulses are transmitted into the water. As explain before the change in phase between the pulse pair is measured so that each pulse pair produces a single velocity estimate and thus the pair is defined as a ping. The time between the two pulses determines the maximum velocity detectable and also determines the maximum range of the system. There is no other acoustic method that can produce such high precision velocity data with such small cells and rapid sampling (Sontek, 2004), this technique is used by ADV (Acoustic Doppler Velocimeters) and is available in certain Doppler Profilers from RDI and Sontek. Broadband works by transmitting a series of coded pulses, all in sequence inside a single long pulse, we obtain many echoes from many scatterers, all combined into a single echo. We extract the propagation delay by computing the autocorrelation at the time lag separating the coded pulses. The success of this computation requires that the different echoes from the coded pulses (all buried inside the same echo) be correlated with one another (RDI 1996). The advantage of broadband and pulse coherent modes is that the accuracy of the data is improved enormously in comparison with narrowband.
Three dimensional velocities.
As mention above, each transducer can only measure an along-transducer velocity, so to measure the three components of velocity we will need a minimum of 3 beams. Also because the beams will be measuring different water columns, we will have to assume that there is horizontal homogeneity, which is sensible most of the times in shelf seas and estuaries. I will explain next how to solve the three dimensional velocities in a four beam array, I chose this configuration for simplicity and because this is the only configuration that can be used to calculate Reynolds stresses using the variance method (Stacey et al., 1999, Lu and Lueck, 1999). The method is based on the fact that an ADCP has two pairs of opposing acoustic beams, and that each beam measures a velocity that is actually a weighted sum of the local horizontal and vertical velocities. So that the velocities determined for each beam are given by:
[math]u_1=vsin\theta+wcos\theta; \quad\quad\quad u_2=-vsin\theta+wcos\theta[/math]
[math]u_3=usin\theta+wcos\theta; \quad\quad\quad u_4=-usin\theta+wcos\theta[/math]
where θ is the angle of the acoustic beam from the vertical (20° in this case) and u, v and w are the horizontal and vertical velocity components. So that:
[math]u=\frac{u_3-u_4}{2sin\theta}; \quad \quad v=\frac{u_1-u_2}{2sin\theta}; \quad\quad w=\frac{u_1+u_2}{2cos\theta}=\frac{u_3+u_4}{2cos\theta}[/math]
The variance method to calculate Reynolds stresses, turbulence production, eddy viscosity and drag coefficients
Separating the velocities into mean and fluctuating quantities and taking the difference between the two opposing beams it can be shown by combining the the equation and ensemble average them that:
<math><{u\prime w\prime}>=\frac{{<u\prime_3^2>}-{<u\prime _4^2>}}{4sin\theta cos\theta}